浙教版第五章专题-梯形辅助线的做法

课件15张PPT。
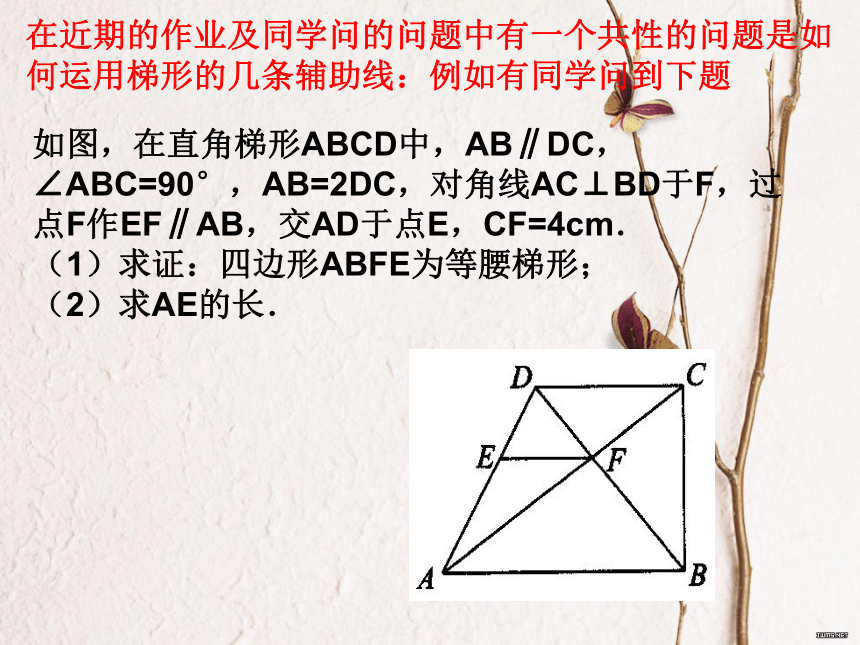
梯形专题在近期的作业及同学问的问题中有一个共性的问题是如何运用梯形的几条辅助线：例如有同学问到下题如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=2DC，对角线AC⊥BD于F，过点F作EF∥AB，交AD于点E，CF=4cm．
（1）求证：四边形ABFE为等腰梯形；
（2）求AE的长．
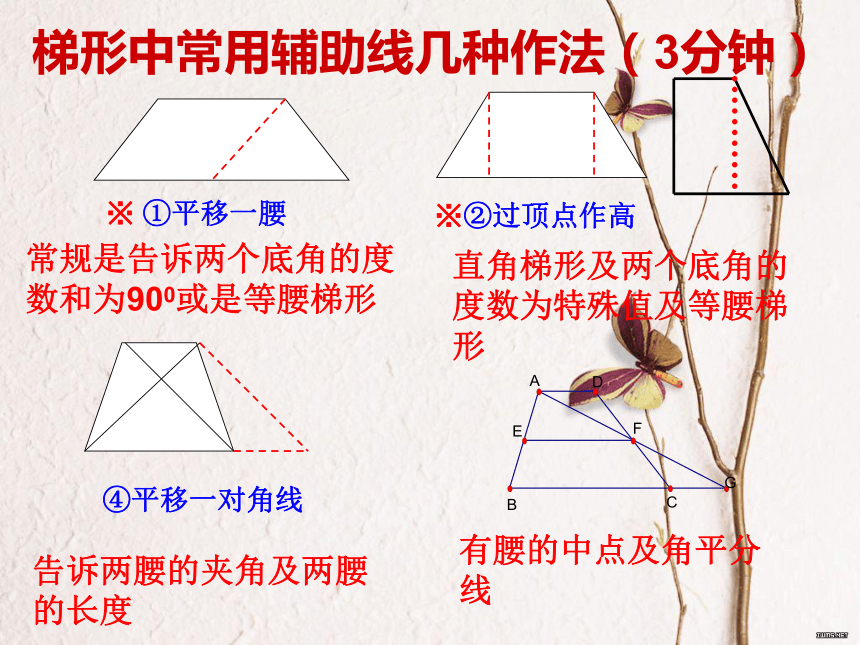
1．梯形几种辅助线形式
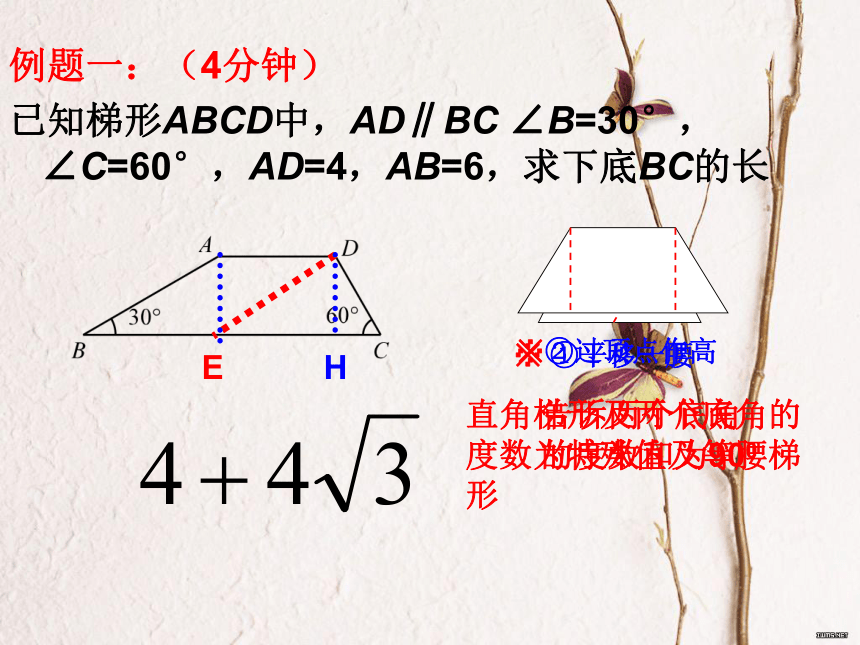
2.会灵活应用梯形几种辅助线学习目标：(1分钟)梯形中常用辅助线几种作法（3分钟）常规是告诉两个底角的度数和为900或是等腰梯形直角梯形及两个底角的度数为特殊值及等腰梯形告诉两腰的夹角及两腰的长度有腰的中点及角平分线例题一：（4分钟）
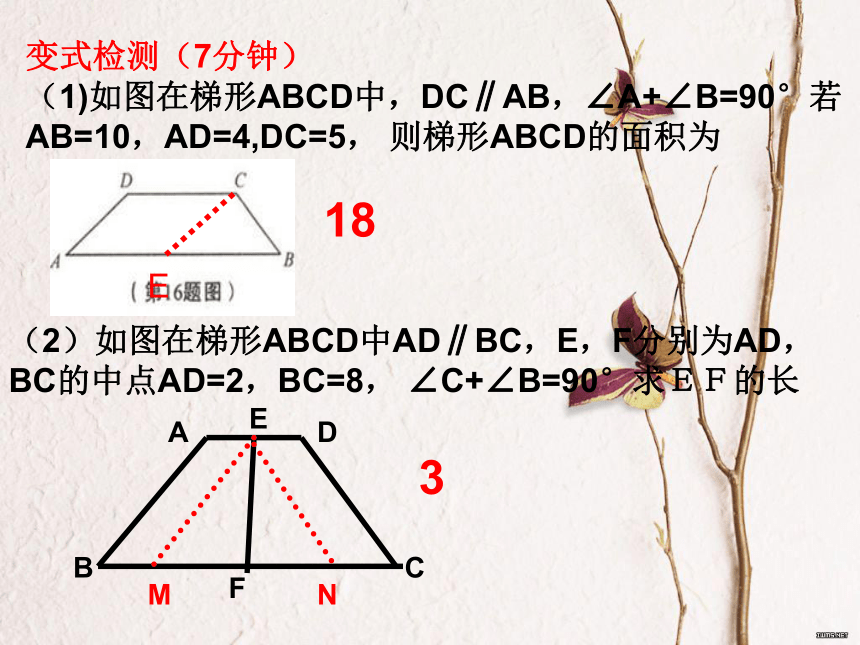
已知梯形ABCD中，AD∥BC ∠B=30°，∠C=60°，AD=4，AB=6，求下底BC的长E告诉两个底角的度数和为900直角梯形及两个底角的度数为特殊值及等腰梯形H变式检测（7分钟）
（1)如图在梯形ABCD中，DC∥AB，∠A+∠B=90°若AB=10，AD=4,DC=5， 则梯形ABCD的面积为 E（2）如图在梯形ABCD中AD∥BC，E，F分别为AD，BC的中点AD=2，BC=8， ∠C+∠B=90°求ＥＦ的长ADBCEFMN1833):如图，在梯形ABCD中，AD∥BC，∠BAD＝90°，AD＋AB＝14，（AB＞AD）BD＝10，BD＝DC，E、F分别是BC、CD上的点，且CE＋CF＝4。
（1）求BC的长；
（2）设EC的长为x，四边形AEFD的面积为y，求y关于x的函数关系式；H12直角梯形及两个底角的度数为特殊值及等腰梯形例题二（5分钟）
如果连接梯形两腰的中点，梯形ABCD中，AD∥BC、点E、F分别为两腰AB、CD的中点
(1)求证EF= （AD+BC ）
ADcBEFG有腰的中点及角平分线mO告诉两对角线的夹角或两对角线及上下底的长度（2）若EF=BM=DM=5，AD+BC=10求∠BOC的度数变式训练：（7分钟）
（1）如图在梯形ABCD中AD∥BC，E为CD的中点，BE平分∠ABC
求证AE⊥BEADBCEF（2）如图在梯形ABCD中AD∥BC，AC=BD=5，
(1)若 AC⊥BD，求梯形ABCD的面积
2）若 AC与BD的夹角为60度，求梯形ABCD的面积OE3、已知四边形ABCD是梯形，AB∥DC，对角线AC=6，BD=8，AB+DC=10。
求∠AOB的度数及梯形ABCD 面积；
OE告诉两对角线的夹角或两对角线及上下底的长度如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=2DC，对角线AC⊥BD于F，过点F作EF∥AB，交AD于点E，CF=4cm．
（1）求证：四边形ABFE为等腰梯形；
（2）求AE的长．
H问题解决（2分钟）当堂训练：11分钟 2、如图，在梯形ABCD中，AD∥BC，AB=DC，∠B=60o，DE∥AB。
求证：（1）DE=DC；（2）△DEC是等边三角形。1、如图，在直角梯形ABCD中，AD∥BC，∠B=90°，E为AB上一点，且ED平分∠ADC，EC平分∠BCD，则下列结论中正确的有（ ）
A、∠ADE=∠CDE B、DE⊥EC
C、AD·BC=BE·DE D、CD=AD+BC
3，已知，如图所示的等腰梯形ABCD中，
AD∥BC，AC⊥BD，AD+BC=10，DE⊥BC
于E，求DE的长. 告诉两对角线的夹角或两对角线及上下底的长度4,如图，梯形ABCD中，AD∥BC，AB=AD=DC，E为底边BC的中点，且DE∥AB，试判断△ADE的形状，并给出证明．5,如图，直角，梯形ABCD中AD∥BC，AB⊥BC，AD=2，BC=3，将腰CD以D为中心逆时针旋转90°至ED，连AE、CE，求 △ADE的面积是多少？7．如图，在梯形ABCD中，AB∥CD，∠A＝90°，AB＝3，CD＝6，BE⊥BC交直线AD于点E．
（1）当点E与D恰好重合时，求AD的长；
（2）当点E在边AD上时（E不与A、D重合），设AD＝x，ED＝y，求y关于x的函数关系式，并写出自变量x取值范围；
（3）是否可能使△ABE、△CDE与△BCE都相似？若能，请求出此时AD的长；若不能，请说明理由（6）如图，矩形纸片ABCD中，AD=9，AB=3，将其折叠，使点D与点B重合，折痕为 EF，求折痕EF的长H