2.2解一元二次方程的解法(4) 课件(共17张PPT)
文档属性
| 名称 | 2.2解一元二次方程的解法(4) 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 588.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-03 09:27:16 | ||
图片预览






文档简介
(共17张PPT)
★一除、二移、三配、四化、五解.
“配方法”解方程的基本步骤:
4、利用开平方法求出原方程的两个解.
3、把方程的左边配成一个完全平方式;
2、把常数项移到方程的右边;
1、把二次项系数化为1(方程的两边同时除以二次项系数a)
你能用配方法解一般形式的一元二次方程ax2+bx+c=0(a≠0)吗?
用配方法解一般形式的一元二次方程
把方程两边都除以
解:
移项,得
配方,得
即
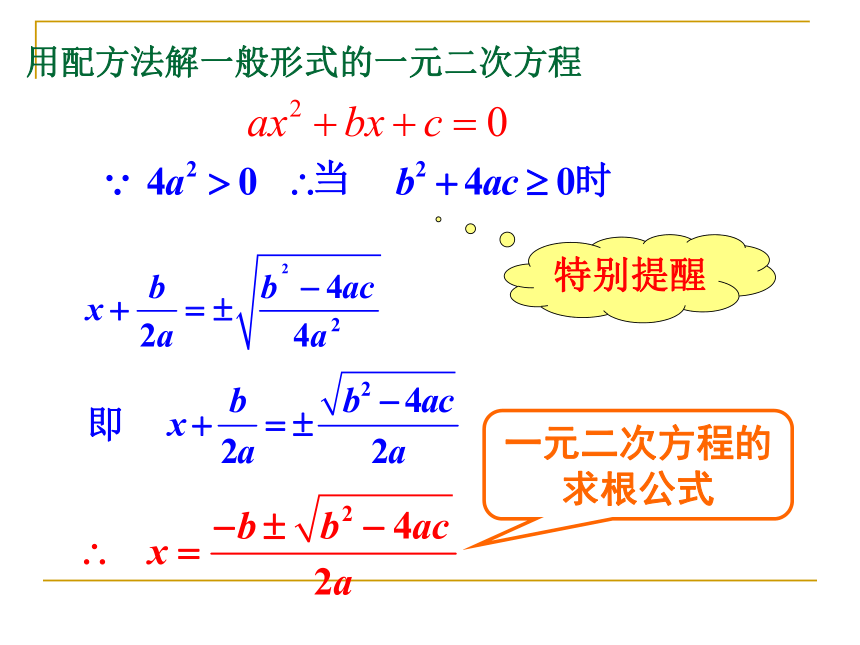
用配方法解一般形式的一元二次方程
当
时
即
一元二次方程的求根公式
特别提醒
一般地,对于一元二次方程 (其中a不为0),如果 ,那么方程的两个根为
这个公式叫做一元二次方程的求根公式.利用求根公式,我们可以 由一元二次方程的系数 的值,直接求得方程的根.这种解一元二次方程的方法叫做公式法.
例8,用公式法解下列一元二次方程:
用公式法解一元二次方程的一般步骤:
3、代入求根公式 :
2、求出 的值,
1、把方程化成一般形式,并写出 的值。
4、写出方程的解:
特别注意:当 时无解
随堂练习
用判别式判别下列方程根的情况(不要求解方程):
例9,解方程:
你能用因式分解法解本例的方程吗?
你能用配方法解本例的方程吗?
解:去括号,得
化简得,
则
∴
即
用公式法解下列方程:
(1)
(2)
(3)
随堂练习
练习:选择适当的方法解下列方程
当 时,方程有两个相等的实数根;
观察以上你所解的方程,方程根的情况与b2-4ac的值的关系如何?
方程有两个不相等的实数根
方程没有实数根
1、 m取什么值时,方程 x2+(2m+1)x+m2-4=0有两个相等的实数解
思考题
2、关于x的一元二次方程ax2+bx+c=0 (a≠0)。 当a,b,c 满足什么条件时,方程的两根为互为相反数?
★一除、二移、三配、四化、五解.
“配方法”解方程的基本步骤:
4、利用开平方法求出原方程的两个解.
3、把方程的左边配成一个完全平方式;
2、把常数项移到方程的右边;
1、把二次项系数化为1(方程的两边同时除以二次项系数a)
你能用配方法解一般形式的一元二次方程ax2+bx+c=0(a≠0)吗?
用配方法解一般形式的一元二次方程
把方程两边都除以
解:
移项,得
配方,得
即
用配方法解一般形式的一元二次方程
当
时
即
一元二次方程的求根公式
特别提醒
一般地,对于一元二次方程 (其中a不为0),如果 ,那么方程的两个根为
这个公式叫做一元二次方程的求根公式.利用求根公式,我们可以 由一元二次方程的系数 的值,直接求得方程的根.这种解一元二次方程的方法叫做公式法.
例8,用公式法解下列一元二次方程:
用公式法解一元二次方程的一般步骤:
3、代入求根公式 :
2、求出 的值,
1、把方程化成一般形式,并写出 的值。
4、写出方程的解:
特别注意:当 时无解
随堂练习
用判别式判别下列方程根的情况(不要求解方程):
例9,解方程:
你能用因式分解法解本例的方程吗?
你能用配方法解本例的方程吗?
解:去括号,得
化简得,
则
∴
即
用公式法解下列方程:
(1)
(2)
(3)
随堂练习
练习:选择适当的方法解下列方程
当 时,方程有两个相等的实数根;
观察以上你所解的方程,方程根的情况与b2-4ac的值的关系如何?
方程有两个不相等的实数根
方程没有实数根
1、 m取什么值时,方程 x2+(2m+1)x+m2-4=0有两个相等的实数解
思考题
2、关于x的一元二次方程ax2+bx+c=0 (a≠0)。 当a,b,c 满足什么条件时,方程的两根为互为相反数?
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
