【新课标】3.4简单几何体的表面展开图(1) 课件(共29张PPT)
文档属性
| 名称 | 【新课标】3.4简单几何体的表面展开图(1) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 14:23:38 | ||
图片预览






文档简介
(共29张PPT)
3.4简单几何体的表面展开图(1)
浙教版九年级下册
教学目标
1.了解几何体表面展开图的概念,会画简单直棱柱的表面展开图.
2.会在简单情况下判断一个平面图形是不是直棱柱的表面展开图.
3.通过折叠,展开等实际操作,感受、体验立体图形与平面图形的关系,能识别常见立体图形展开图的形状.
教学重难点
重点:
会画立方体的表面展开图.
难点:
能利用直棱柱的表面展开图进行相关计算.
新知导入
杜登尼是19世纪英国知名的谜题创作者,下面的问题来源于他创作的“蜘蛛和苍蝇”问题:
在一个长、宽、高分别为3米,2米,2米的长方体房间内,一只蜘蛛在一面墙的中间,离天花板0.1米处(点A处),苍蝇在对面墙的中间,离地面0.1米处(点B处).
试问,蜘蛛去捉苍蝇需要爬行的最短路程是多少?
新知导入
解决立体图形上最短路径问题:
基本思路:
立体图形
即化“曲”为“直”
平面图形
想一想:怎样将立体图形转化为平面图形?
新知讲解
小组合作:分别将三个立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,你能得到下列图形吗?
新知讲解
像上图那样,将几何体沿着某些棱“剪”开,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图。
【做一做】将一个立方体纸盒沿某些棱剪开,你还能得到其他不同的展开图吗?
新知讲解
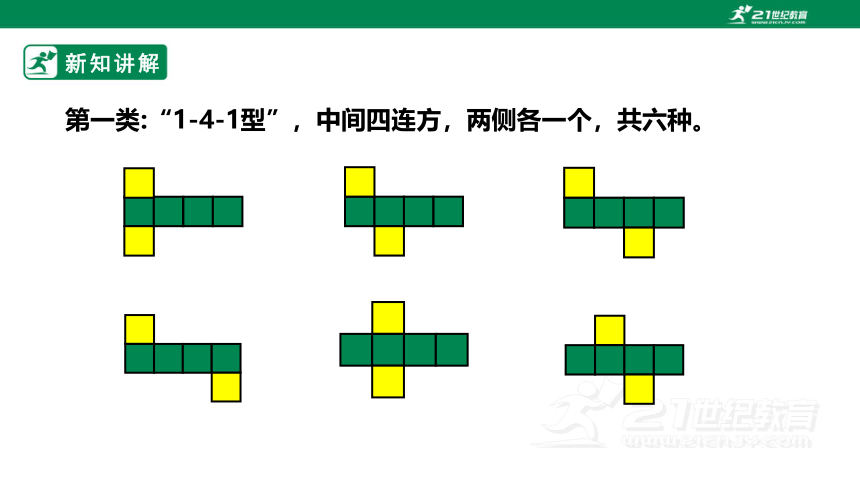
第一类:“1-4-1型”,中间四连方,两侧各一个,共六种。
新知讲解
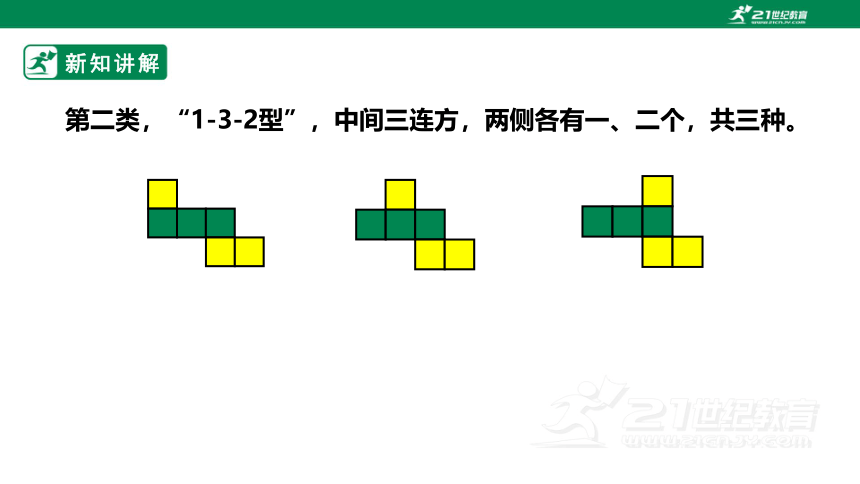
第二类,“1-3-2型”,中间三连方,两侧各有一、二个,共三种。
新知讲解
第三类,“2-2-2型”,中间二连方,两侧各有二个,只有一种。
第四类,“3-3型”,两排各三个,只有一种。
新知讲解
【总结归纳】
正方体是一个特殊的四棱柱,它的所有棱长都相等,所有面都是正方形且大小相等,将正方体的表面沿某些棱剪开,展成一个平面图形,其展开图共有11种形式.
【拓展】
正方体11种展开图助记口诀:
一四一,二三一,一在一侧任意移;二二二,阶梯路;二个三,日相连。
新知讲解
【例1】下图是一个立方体的表面展开图吗?如果是,分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示法)。
分析:可以先用折叠的方法试一试,看它能否折成一个立方体。
新知讲解
解:上图是一个立方体的表面展开图,各对应面上的数字表示如图1和图2.
图1
图2
新知讲解
【做一做】
下列各图中,哪些图能折叠成一个立方体?动手试一试.
能
能
不能
新知讲解
【总结归纳】不能折成正方体的几种情况:
新知讲解
【例2】如图1,为了生产这种牛奶包装盒,需要先画出展开图纸样.
(1)如图2给出三种纸样,它们都正确吗?
图1
图2
正确
不正确
正确
新知讲解
(2)从图2正确的纸样中选出一种,标注上尺寸.
解:根据图2,若选图甲,可得表面展开图及尺寸标注如下图所示.
新知讲解
(3) 利用你所选的一种纸样,求出包装盒的侧面积和全面积(侧面积与两个底面积的和).
解:如图所示,包装盒的侧面积和全面积为:
S侧=(b+a+b+a)h
=2ah+2bh;
S表=S侧+2S底
=2ah+2bh+2ab.
课堂练习
1.观察下列图形,其中是正方体的表面展开图的是( ).
C
课堂练习
2.如图,可以折叠成一个无盖正方体盒子的是( )
A.只有① B.①②
C.②③ D.①③
D
课堂练习
3.下图中经过折叠可以围成一个直棱柱的是( )
B
课堂练习
4.下图是正方体的展开图,还原成正方体后,其中完全一样的是( )
A.(1)和(2)
B.(1)和(3)
C.(2)和(3)
D.(3)和(4)
D
课堂练习
5.把如图所示的图形折成正方体,如果相对面的值相等,则2a-x+3y的值为( ) .
A. 7
B. 8
C. 9
D. 10
A
课堂练习
6.如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ;b= ;c= .
c
5
-2
b
a
3
2
-5
-3
课堂总结
本节课你学到了什么?
1.将几何体沿着某些棱“剪”开,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图。
2.正方体是一个特殊的四棱柱,它的所有棱长都相等,所有面都是正方形且大小相等,将正方体的表面沿某些棱剪开,展成一个平面图形,其展开图共有11种形式.
板书设计
课题:3.4简单几何体的表面展开图(1)
教师板演区
学生展示区
一、几何体的表面展开图
二、正方体的表面展开图
三、例题讲解
作业布置
课本 P80 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4简单几何体的表面展开图(1)
浙教版九年级下册
教学目标
1.了解几何体表面展开图的概念,会画简单直棱柱的表面展开图.
2.会在简单情况下判断一个平面图形是不是直棱柱的表面展开图.
3.通过折叠,展开等实际操作,感受、体验立体图形与平面图形的关系,能识别常见立体图形展开图的形状.
教学重难点
重点:
会画立方体的表面展开图.
难点:
能利用直棱柱的表面展开图进行相关计算.
新知导入
杜登尼是19世纪英国知名的谜题创作者,下面的问题来源于他创作的“蜘蛛和苍蝇”问题:
在一个长、宽、高分别为3米,2米,2米的长方体房间内,一只蜘蛛在一面墙的中间,离天花板0.1米处(点A处),苍蝇在对面墙的中间,离地面0.1米处(点B处).
试问,蜘蛛去捉苍蝇需要爬行的最短路程是多少?
新知导入
解决立体图形上最短路径问题:
基本思路:
立体图形
即化“曲”为“直”
平面图形
想一想:怎样将立体图形转化为平面图形?
新知讲解
小组合作:分别将三个立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平,你能得到下列图形吗?
新知讲解
像上图那样,将几何体沿着某些棱“剪”开,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图。
【做一做】将一个立方体纸盒沿某些棱剪开,你还能得到其他不同的展开图吗?
新知讲解
第一类:“1-4-1型”,中间四连方,两侧各一个,共六种。
新知讲解
第二类,“1-3-2型”,中间三连方,两侧各有一、二个,共三种。
新知讲解
第三类,“2-2-2型”,中间二连方,两侧各有二个,只有一种。
第四类,“3-3型”,两排各三个,只有一种。
新知讲解
【总结归纳】
正方体是一个特殊的四棱柱,它的所有棱长都相等,所有面都是正方形且大小相等,将正方体的表面沿某些棱剪开,展成一个平面图形,其展开图共有11种形式.
【拓展】
正方体11种展开图助记口诀:
一四一,二三一,一在一侧任意移;二二二,阶梯路;二个三,日相连。
新知讲解
【例1】下图是一个立方体的表面展开图吗?如果是,分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示法)。
分析:可以先用折叠的方法试一试,看它能否折成一个立方体。
新知讲解
解:上图是一个立方体的表面展开图,各对应面上的数字表示如图1和图2.
图1
图2
新知讲解
【做一做】
下列各图中,哪些图能折叠成一个立方体?动手试一试.
能
能
不能
新知讲解
【总结归纳】不能折成正方体的几种情况:
新知讲解
【例2】如图1,为了生产这种牛奶包装盒,需要先画出展开图纸样.
(1)如图2给出三种纸样,它们都正确吗?
图1
图2
正确
不正确
正确
新知讲解
(2)从图2正确的纸样中选出一种,标注上尺寸.
解:根据图2,若选图甲,可得表面展开图及尺寸标注如下图所示.
新知讲解
(3) 利用你所选的一种纸样,求出包装盒的侧面积和全面积(侧面积与两个底面积的和).
解:如图所示,包装盒的侧面积和全面积为:
S侧=(b+a+b+a)h
=2ah+2bh;
S表=S侧+2S底
=2ah+2bh+2ab.
课堂练习
1.观察下列图形,其中是正方体的表面展开图的是( ).
C
课堂练习
2.如图,可以折叠成一个无盖正方体盒子的是( )
A.只有① B.①②
C.②③ D.①③
D
课堂练习
3.下图中经过折叠可以围成一个直棱柱的是( )
B
课堂练习
4.下图是正方体的展开图,还原成正方体后,其中完全一样的是( )
A.(1)和(2)
B.(1)和(3)
C.(2)和(3)
D.(3)和(4)
D
课堂练习
5.把如图所示的图形折成正方体,如果相对面的值相等,则2a-x+3y的值为( ) .
A. 7
B. 8
C. 9
D. 10
A
课堂练习
6.如图是一个立方体纸盒的展开图,使展开图沿虚线折叠成正方体后相对面上的两个数互为相反数,求:a= ;b= ;c= .
c
5
-2
b
a
3
2
-5
-3
课堂总结
本节课你学到了什么?
1.将几何体沿着某些棱“剪”开,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图。
2.正方体是一个特殊的四棱柱,它的所有棱长都相等,所有面都是正方形且大小相等,将正方体的表面沿某些棱剪开,展成一个平面图形,其展开图共有11种形式.
板书设计
课题:3.4简单几何体的表面展开图(1)
教师板演区
学生展示区
一、几何体的表面展开图
二、正方体的表面展开图
三、例题讲解
作业布置
课本 P80 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
