【核心素养目标】3.4简单几何体的表面展开图(2) 教学设计
文档属性
| 名称 | 【核心素养目标】3.4简单几何体的表面展开图(2) 教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版九年级下册数学3.4简单几何体的表面展开图(2)教学设计
课题 3.4简单几何体的表面展开图(2) 单元 第3单元 学科 数学 年级 九
教材分析 本节课是浙教版九年级下册数学第3章第4节第2课时的内容,立体图形的展开图是从学生生活周围熟悉的物体入手,使学生进一步认识立体图形与平面图形的关系;本节课要让学生了解圆柱由哪些平面图形围成,更重要的是让学生通过观察、思考和自己动手操作,经历和体验图形的变化过程,使学生了解研究立体图形展开图的方法。
核心素养分析 通过本节课的教学,改变课程过于注重知识传授的倾向,强调形成积极主动的学习态度,关注学生的学习兴趣和经验,实施开放式教学,让学生主动参与学习活动,并引导学生在课堂活动中感悟知识的生成、发展与变化。
学习目标 1.通过动手操作了解圆柱展开图的特征.2.了解圆柱的侧面、底面、母线等概念.3.会计算圆柱的侧面积或全面积.
重点 了解圆柱展开图的特征和圆柱的侧面、底面、母线等概念及其特征.
难点 会用展开图的面积公式计算圆柱的侧面积和全面积.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 想一想:什么是几何体的表面展开图?将几何体沿着某些棱“剪”开,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图。正方体有几种表面展开图?正方体有11种展开图. 学生复习上节课所学知识,回答问题。 通过复习,激发学生学习动机和兴趣,吸引学生注意力,为引进新知识的学习做好心理准备。
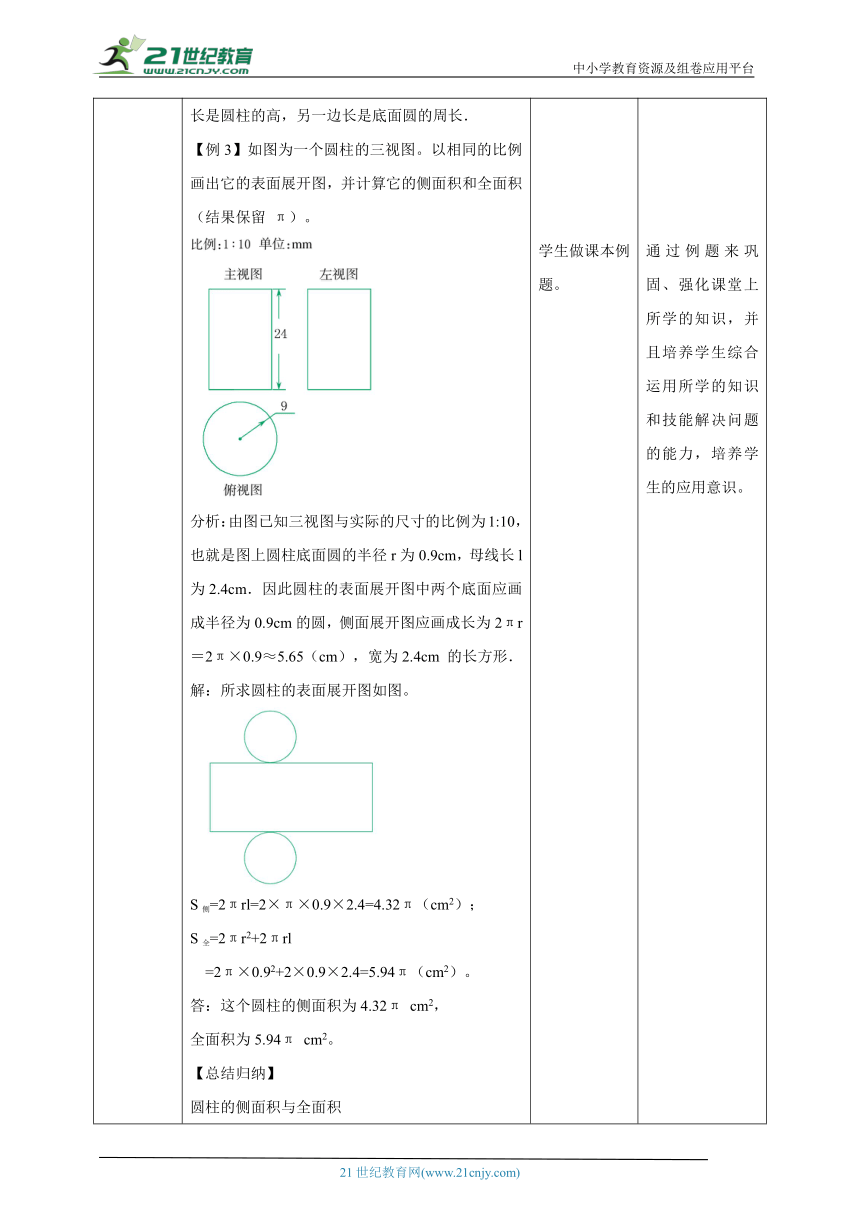
讲授新课 下面我们来探讨圆柱的表面展开图.如图,圆柱可以看做由一个矩形绕它的一条边(BC)旋转一周,其余各边所成的面围成的几何体.AB,CD 旋转所成的面就是圆柱的两个底面,是两个半径相同的圆。 AD 旋转所成的面就是圆柱的侧面。AD 不论转动到哪个位置,都是圆柱的母线。【做一做】按照如图所示的方法把圆柱的侧面展开,会得到什么图形?如果沿圆柱的任意一条母线(MN)把圆柱的侧面“剪开”,铺平,那么就得到圆柱的侧面展开图,如下图,这个侧面展开图是一个矩形(矩形 ABCD).这个矩形的一条边(AD)等于圆柱的母线长,也就等于圆柱的高,另一条与它相邻的边(AB)等于底面圆的周长. 【想一想】如果将圆柱的表面展开,会得到什么图形? 一般地,一个底面半径为 r,母线长为 l 的圆柱的表面展开图如图所示.圆柱的表面展开图是由两个大小相同的圆(底面)和一个长方形(侧面)组成的,其中侧面展开图的一边长是圆柱的高,另一边长是底面圆的周长.【例3】如图为一个圆柱的三视图。以相同的比例画出它的表面展开图,并计算它的侧面积和全面积(结果保留 π)。分析:由图已知三视图与实际的尺寸的比例为1:10,也就是图上圆柱底面圆的半径r为0.9cm,母线长l为2.4cm.因此圆柱的表面展开图中两个底面应画成半径为0.9cm的圆,侧面展开图应画成长为2πr=2π×0.9≈5.65(cm),宽为2.4cm 的长方形.解:所求圆柱的表面展开图如图。S侧=2πrl=2×π×0.9×2.4=4.32π(cm2);S全=2πr2+2πrl =2π×0.92+2×0.9×2.4=5.94π(cm2)。答:这个圆柱的侧面积为4.32π cm2,全面积为5.94π cm2。【总结归纳】圆柱的侧面积与全面积侧面展开图:长为圆柱底面圆周长,宽为圆柱母线长的长方形.侧面积=展开图长方形的面积.全面积=侧面积+底面积.【探究活动】如图,一只蚂蚁在圆柱的底面 A 处,想爬到对面 B 处,它怎样爬行路线最近?先说说你的解题思路,然后给出解答,并算出最近的路线的长(精确到0.01cm).解:画出圆柱的侧面展开图如图。根据两点之间线段最短,蚂蚁在圆柱表面爬行的最短路程长应是展开图上AB两点之间的距离AB。由题意得,AC=6cm,BC=2π.由勾股定理可得:答:最近路线的长为8.64cm.【总结归纳】解决此类问题,应先把圆柱体的侧面沿着它的一条高展开,得到一个长方形,然后通过两点之间,线段最短,构造直角三角形,再利用勾股定理求出斜边的长度。 学生探究圆柱的组成部分。学生动手操作,探究圆柱的展开图。学生做课本例题。学生根据所学知识探究在圆柱上的最短路程问题。 让学生自由组合成小组进行操作活动,培养学生动脑猜想、动手操作实验的良好习惯及合作交流的精神。在教学中运用探究式教学模式,使学生体验教学再创造的思维过程,培养学生的创造意识和科学精神。通过例题来巩固、强化课堂上所学的知识,并且培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识。从有趣的生活场景引入,激发学生的探究欲望,这样既能提高学生解决问题兴趣,又培养学生观察、分析、归纳问题、逻辑理解的能力。
课堂练习 1.下图是一个几何体的表面展开图,该几何体是( C ).A.棱柱 B.棱锥 C.圆柱 D.圆锥2.一个几何体的三视图如图,则其侧面积为( D ).A.500π B.300π C.100π D.200π3.一个几何体的三视图如图所示,则该几何体的全面积是__48π+64_(结果保留π).4.如图,圆柱的底面周长为16,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S处,则移动的最短距离为( A ) .A.10 B.12 C.14 D.205.如图是从三个方向看一个几何体所得到的图形.(1)写出这个几何体的名称;解:这个几何体是圆柱.(2)若从正面看得到的矩形的长为10 cm,从上面看得到的圆的直径为4 cm,求这个几何体的全面积(结果保留π).解:∵从正面看得到的矩形的长为10cm,从上面看得到的圆的直径为4cm,∴该圆柱的底面半径r为2cm,母线l为10cm.∴这个几何体的全面积为2πrl+2πr2=2π×2×10+2π×22=48π(cm2).答:这个几何体的全面积为48π cm2. 学生做练习,教师订正答案。 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 本节课你学到了什么?1.圆柱的表面展开图是由两个大小相同的圆(底面)和一个长方形(侧面)组成的,其中侧面展开图的一边长是圆柱的高,另一边长是底面圆的周长.2.解决圆柱的最短路程问题,应先把圆柱体的侧面沿着它的一条高展开,得到一个长方形,然后通过两点之间,线段最短,构造直角三角形,再利用勾股定理求出斜边的长度。 学生在教师的引导下总结归纳。 充分发挥学生的主体作用,有助于学生在理解新知识的基础上,及时把知识系统化,条理化。
板书 课题:3.4简单几何体的表面展开图(2)一、圆柱的表面展开图二、圆柱的侧面积和全面积 三、圆柱的最短路程
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
浙教版九年级下册数学3.4简单几何体的表面展开图(2)教学设计
课题 3.4简单几何体的表面展开图(2) 单元 第3单元 学科 数学 年级 九
教材分析 本节课是浙教版九年级下册数学第3章第4节第2课时的内容,立体图形的展开图是从学生生活周围熟悉的物体入手,使学生进一步认识立体图形与平面图形的关系;本节课要让学生了解圆柱由哪些平面图形围成,更重要的是让学生通过观察、思考和自己动手操作,经历和体验图形的变化过程,使学生了解研究立体图形展开图的方法。
核心素养分析 通过本节课的教学,改变课程过于注重知识传授的倾向,强调形成积极主动的学习态度,关注学生的学习兴趣和经验,实施开放式教学,让学生主动参与学习活动,并引导学生在课堂活动中感悟知识的生成、发展与变化。
学习目标 1.通过动手操作了解圆柱展开图的特征.2.了解圆柱的侧面、底面、母线等概念.3.会计算圆柱的侧面积或全面积.
重点 了解圆柱展开图的特征和圆柱的侧面、底面、母线等概念及其特征.
难点 会用展开图的面积公式计算圆柱的侧面积和全面积.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 想一想:什么是几何体的表面展开图?将几何体沿着某些棱“剪”开,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图。正方体有几种表面展开图?正方体有11种展开图. 学生复习上节课所学知识,回答问题。 通过复习,激发学生学习动机和兴趣,吸引学生注意力,为引进新知识的学习做好心理准备。
讲授新课 下面我们来探讨圆柱的表面展开图.如图,圆柱可以看做由一个矩形绕它的一条边(BC)旋转一周,其余各边所成的面围成的几何体.AB,CD 旋转所成的面就是圆柱的两个底面,是两个半径相同的圆。 AD 旋转所成的面就是圆柱的侧面。AD 不论转动到哪个位置,都是圆柱的母线。【做一做】按照如图所示的方法把圆柱的侧面展开,会得到什么图形?如果沿圆柱的任意一条母线(MN)把圆柱的侧面“剪开”,铺平,那么就得到圆柱的侧面展开图,如下图,这个侧面展开图是一个矩形(矩形 ABCD).这个矩形的一条边(AD)等于圆柱的母线长,也就等于圆柱的高,另一条与它相邻的边(AB)等于底面圆的周长. 【想一想】如果将圆柱的表面展开,会得到什么图形? 一般地,一个底面半径为 r,母线长为 l 的圆柱的表面展开图如图所示.圆柱的表面展开图是由两个大小相同的圆(底面)和一个长方形(侧面)组成的,其中侧面展开图的一边长是圆柱的高,另一边长是底面圆的周长.【例3】如图为一个圆柱的三视图。以相同的比例画出它的表面展开图,并计算它的侧面积和全面积(结果保留 π)。分析:由图已知三视图与实际的尺寸的比例为1:10,也就是图上圆柱底面圆的半径r为0.9cm,母线长l为2.4cm.因此圆柱的表面展开图中两个底面应画成半径为0.9cm的圆,侧面展开图应画成长为2πr=2π×0.9≈5.65(cm),宽为2.4cm 的长方形.解:所求圆柱的表面展开图如图。S侧=2πrl=2×π×0.9×2.4=4.32π(cm2);S全=2πr2+2πrl =2π×0.92+2×0.9×2.4=5.94π(cm2)。答:这个圆柱的侧面积为4.32π cm2,全面积为5.94π cm2。【总结归纳】圆柱的侧面积与全面积侧面展开图:长为圆柱底面圆周长,宽为圆柱母线长的长方形.侧面积=展开图长方形的面积.全面积=侧面积+底面积.【探究活动】如图,一只蚂蚁在圆柱的底面 A 处,想爬到对面 B 处,它怎样爬行路线最近?先说说你的解题思路,然后给出解答,并算出最近的路线的长(精确到0.01cm).解:画出圆柱的侧面展开图如图。根据两点之间线段最短,蚂蚁在圆柱表面爬行的最短路程长应是展开图上AB两点之间的距离AB。由题意得,AC=6cm,BC=2π.由勾股定理可得:答:最近路线的长为8.64cm.【总结归纳】解决此类问题,应先把圆柱体的侧面沿着它的一条高展开,得到一个长方形,然后通过两点之间,线段最短,构造直角三角形,再利用勾股定理求出斜边的长度。 学生探究圆柱的组成部分。学生动手操作,探究圆柱的展开图。学生做课本例题。学生根据所学知识探究在圆柱上的最短路程问题。 让学生自由组合成小组进行操作活动,培养学生动脑猜想、动手操作实验的良好习惯及合作交流的精神。在教学中运用探究式教学模式,使学生体验教学再创造的思维过程,培养学生的创造意识和科学精神。通过例题来巩固、强化课堂上所学的知识,并且培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识。从有趣的生活场景引入,激发学生的探究欲望,这样既能提高学生解决问题兴趣,又培养学生观察、分析、归纳问题、逻辑理解的能力。
课堂练习 1.下图是一个几何体的表面展开图,该几何体是( C ).A.棱柱 B.棱锥 C.圆柱 D.圆锥2.一个几何体的三视图如图,则其侧面积为( D ).A.500π B.300π C.100π D.200π3.一个几何体的三视图如图所示,则该几何体的全面积是__48π+64_(结果保留π).4.如图,圆柱的底面周长为16,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S处,则移动的最短距离为( A ) .A.10 B.12 C.14 D.205.如图是从三个方向看一个几何体所得到的图形.(1)写出这个几何体的名称;解:这个几何体是圆柱.(2)若从正面看得到的矩形的长为10 cm,从上面看得到的圆的直径为4 cm,求这个几何体的全面积(结果保留π).解:∵从正面看得到的矩形的长为10cm,从上面看得到的圆的直径为4cm,∴该圆柱的底面半径r为2cm,母线l为10cm.∴这个几何体的全面积为2πrl+2πr2=2π×2×10+2π×22=48π(cm2).答:这个几何体的全面积为48π cm2. 学生做练习,教师订正答案。 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 本节课你学到了什么?1.圆柱的表面展开图是由两个大小相同的圆(底面)和一个长方形(侧面)组成的,其中侧面展开图的一边长是圆柱的高,另一边长是底面圆的周长.2.解决圆柱的最短路程问题,应先把圆柱体的侧面沿着它的一条高展开,得到一个长方形,然后通过两点之间,线段最短,构造直角三角形,再利用勾股定理求出斜边的长度。 学生在教师的引导下总结归纳。 充分发挥学生的主体作用,有助于学生在理解新知识的基础上,及时把知识系统化,条理化。
板书 课题:3.4简单几何体的表面展开图(2)一、圆柱的表面展开图二、圆柱的侧面积和全面积 三、圆柱的最短路程
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
