【新课标】3.4简单几何体的表面展开图(3) 课件(共25张PPT)
文档属性
| 名称 | 【新课标】3.4简单几何体的表面展开图(3) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
3.4 简单几何体的表面展开图(3)
浙教版九年级下册
教学目标
1.了解圆锥的侧面、底面、高、母线等概念.
2.了解圆锥侧面展开图的形状.
3.探索并掌握圆锥的侧面积、全面积计算公式.
4.会用圆锥的侧面积计算公式解决实际问题.
教学重难点
重点:
了解圆锥的侧面、底面、高、母线等概念,会计算圆锥的侧面积、全面积。
难点:
会用圆锥的侧面积计算公式解决实际问题。
新知导入
圆柱的表面展开图是什么图形?
圆柱的表面展开图是由两个大小相同的圆(底面)和一个长方形(侧面)组成的,其中侧面展开图的一边长是圆柱的高,另一边长是底面圆的周长.
新知导入
生活中你见过哪些圆锥形状的物体?
新知讲解
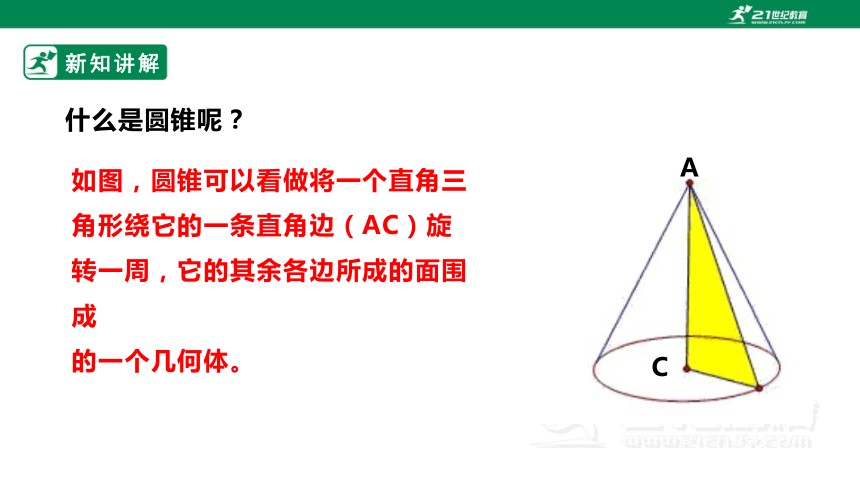
什么是圆锥呢?
如图,圆锥可以看做将一个直角三角形绕它的一条直角边(AC)旋转一周,它的其余各边所成的面围成
的一个几何体。
A
C
新知讲解
圆锥的高:连结圆锥的顶点与底面圆心的线段叫做圆锥的高,如图中的AC。
斜边 AB 不论转动到哪一个位置,都叫做圆锥的母线。
圆锥的母线:圆锥的顶点和底面圆周上任意一点的连线段叫做圆锥的母线,如图中的AB。
新知讲解
直角边 BC 旋转所成的面就是圆锥的底面,圆锥的底面是一个圆。
斜边 AB 旋转所成的面就是圆锥的侧面.
新知讲解
下面我们来探讨圆锥的表面展开图.
(1) 将一个圆锥模型的侧面沿它的一条母线剪开、铺平. 观察所得的平面图形是什么图形.
所得的平面图形是扇形。
新知讲解
(2) 圆锥的底面周长与侧面展开图有什么关系?
将圆锥的侧面沿母线展开,是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长。
新知讲解
(3) 推导圆锥的侧面积公式.
一般地,一个底面半径为r,母线长为l的圆锥的侧面展开图是一个半径为母线长l,弧长为底面圆周长2πr的扇形,如图 .
由此我们可以得到圆锥的侧面积和全面积:
S=πrl.
S=πr2+πrl.
新知讲解
若设圆锥的侧面展开图扇形的圆心角为θ,则由 ,得到圆锥侧面展开图扇形的圆心角度数的计算公式:
新知讲解
例4 圆锥形烟囱帽的母线长为80cm,高为38.7cm。
(1)求这个烟囱帽的面积(精确到103cm)。
解:(1)∵ l=80cm,h=38.7cm,
∴S侧=πrl=π×70×80≈1.8×104(cm2).
答:烟囱帽的面积约1.8×104cm2.
新知讲解
例4 圆锥形烟囱帽的母线长为80cm,高为38.7cm。
(2)以 1 : 40 的比例画出这烟囱帽的展开图.
解:烟囱帽的展开图的扇形圆心角
为θ= ×360°= ×360°=315°.
按1:40的比例画这烟囱帽的展开图
如图所示。
课堂练习
1.丁丁和当当用半径相同的圆形纸片分别剪成扇形(如图)做圆锥形的帽子,则两人做成的帽子的高度相比,( ).
A.丁丁的高
B.当当的高
C.一样高
D.不确定
B
课堂练习
2.已知某几何体的三视图如图所示,则该几何体的侧面展开图的圆心角的度数为( ).
A.214°
B.215°
C.216°
D.217°
C
课堂练习
3.若圆锥的侧面积为18π,底面半径为3,则该圆锥的母线长是________.
6
课堂练习
4.如图,圆锥的高是4,它的侧面展开图是圆心角为120°的扇形,则圆锥的侧面积是______(结果保留π).
6π
课堂练习
5.现有一张圆心角为108°,半径为4 cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1 cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为________.
0.8π cm2
课堂练习
6.如图是一个几体何的三视图(图中尺寸单位:cm),则这个几何体的侧面积为( ).
A.48π cm2
B.24π cm2
C.12π cm2
D.9π cm2
B
课堂总结
本节课你学到了什么?
1.圆锥的高、母线、侧面和底面。
2.圆锥的侧面积和全面积公式。
3.圆锥侧面展开图扇形的圆心角度数的计算公式。
板书设计
课题:3.4 简单几何体的表面展开图(3)
教师板演区
学生展示区
一、圆锥的组成
二、圆锥的侧面积和全面积公式
三、圆心角度数的计算公式
作业布置
课本 P86 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4 简单几何体的表面展开图(3)
浙教版九年级下册
教学目标
1.了解圆锥的侧面、底面、高、母线等概念.
2.了解圆锥侧面展开图的形状.
3.探索并掌握圆锥的侧面积、全面积计算公式.
4.会用圆锥的侧面积计算公式解决实际问题.
教学重难点
重点:
了解圆锥的侧面、底面、高、母线等概念,会计算圆锥的侧面积、全面积。
难点:
会用圆锥的侧面积计算公式解决实际问题。
新知导入
圆柱的表面展开图是什么图形?
圆柱的表面展开图是由两个大小相同的圆(底面)和一个长方形(侧面)组成的,其中侧面展开图的一边长是圆柱的高,另一边长是底面圆的周长.
新知导入
生活中你见过哪些圆锥形状的物体?
新知讲解
什么是圆锥呢?
如图,圆锥可以看做将一个直角三角形绕它的一条直角边(AC)旋转一周,它的其余各边所成的面围成
的一个几何体。
A
C
新知讲解
圆锥的高:连结圆锥的顶点与底面圆心的线段叫做圆锥的高,如图中的AC。
斜边 AB 不论转动到哪一个位置,都叫做圆锥的母线。
圆锥的母线:圆锥的顶点和底面圆周上任意一点的连线段叫做圆锥的母线,如图中的AB。
新知讲解
直角边 BC 旋转所成的面就是圆锥的底面,圆锥的底面是一个圆。
斜边 AB 旋转所成的面就是圆锥的侧面.
新知讲解
下面我们来探讨圆锥的表面展开图.
(1) 将一个圆锥模型的侧面沿它的一条母线剪开、铺平. 观察所得的平面图形是什么图形.
所得的平面图形是扇形。
新知讲解
(2) 圆锥的底面周长与侧面展开图有什么关系?
将圆锥的侧面沿母线展开,是一个扇形,这个扇形的弧长等于圆锥底面的周长,而扇形的半径等于圆锥的母线的长。
新知讲解
(3) 推导圆锥的侧面积公式.
一般地,一个底面半径为r,母线长为l的圆锥的侧面展开图是一个半径为母线长l,弧长为底面圆周长2πr的扇形,如图 .
由此我们可以得到圆锥的侧面积和全面积:
S=πrl.
S=πr2+πrl.
新知讲解
若设圆锥的侧面展开图扇形的圆心角为θ,则由 ,得到圆锥侧面展开图扇形的圆心角度数的计算公式:
新知讲解
例4 圆锥形烟囱帽的母线长为80cm,高为38.7cm。
(1)求这个烟囱帽的面积(精确到103cm)。
解:(1)∵ l=80cm,h=38.7cm,
∴S侧=πrl=π×70×80≈1.8×104(cm2).
答:烟囱帽的面积约1.8×104cm2.
新知讲解
例4 圆锥形烟囱帽的母线长为80cm,高为38.7cm。
(2)以 1 : 40 的比例画出这烟囱帽的展开图.
解:烟囱帽的展开图的扇形圆心角
为θ= ×360°= ×360°=315°.
按1:40的比例画这烟囱帽的展开图
如图所示。
课堂练习
1.丁丁和当当用半径相同的圆形纸片分别剪成扇形(如图)做圆锥形的帽子,则两人做成的帽子的高度相比,( ).
A.丁丁的高
B.当当的高
C.一样高
D.不确定
B
课堂练习
2.已知某几何体的三视图如图所示,则该几何体的侧面展开图的圆心角的度数为( ).
A.214°
B.215°
C.216°
D.217°
C
课堂练习
3.若圆锥的侧面积为18π,底面半径为3,则该圆锥的母线长是________.
6
课堂练习
4.如图,圆锥的高是4,它的侧面展开图是圆心角为120°的扇形,则圆锥的侧面积是______(结果保留π).
6π
课堂练习
5.现有一张圆心角为108°,半径为4 cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1 cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为________.
0.8π cm2
课堂练习
6.如图是一个几体何的三视图(图中尺寸单位:cm),则这个几何体的侧面积为( ).
A.48π cm2
B.24π cm2
C.12π cm2
D.9π cm2
B
课堂总结
本节课你学到了什么?
1.圆锥的高、母线、侧面和底面。
2.圆锥的侧面积和全面积公式。
3.圆锥侧面展开图扇形的圆心角度数的计算公式。
板书设计
课题:3.4 简单几何体的表面展开图(3)
教师板演区
学生展示区
一、圆锥的组成
二、圆锥的侧面积和全面积公式
三、圆心角度数的计算公式
作业布置
课本 P86 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
