4.4_平行四边形的判定(2)

课件26张PPT。定理2：两组对边分别相等的四边形是平行四边形说一说：我们已经学过哪些平行四边形的判定方法?定义: 两组对边分别平行的四边形是
平行四边形 知识回顾定理1: 一组对边平行且相等的四边形 平行四边形 4.4平行四边形的判定(2) 学习了平行四边形后，小明回家用细木棒钉制了一个。第二天，小明拿着自己动手做的平行四边形向同学们展示。
问：你不用任何作图工具能确定这四边形就是平行四边形吗？
小丽说：“我可以不用任何作图工具，只要两条细绳就能判断它是不是平行四边形。”
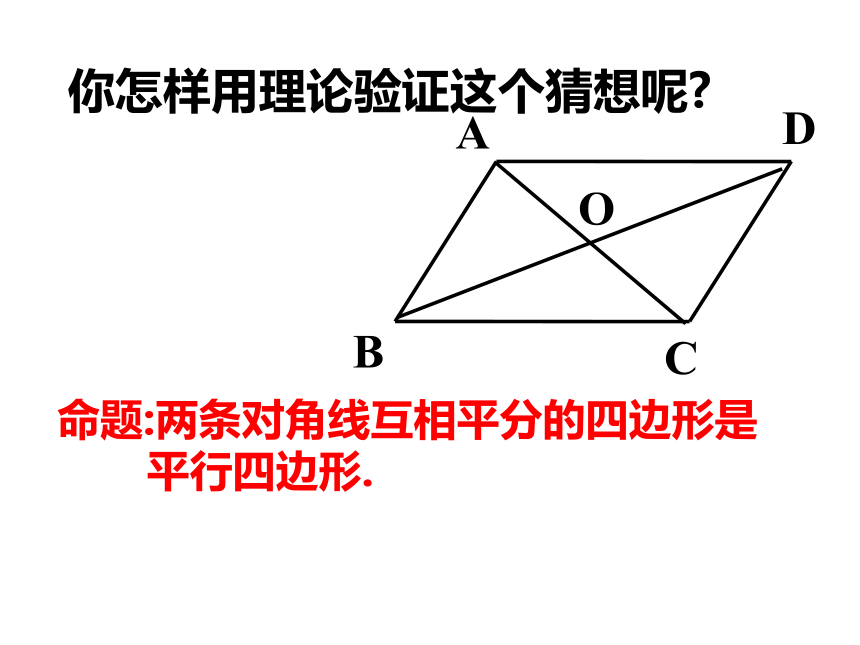
只见小丽用两条细绳做四边形的对角线，并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折，发现它们被记号点分成的两段线段都能重合，小丽高兴地说：“这的确是个平行四边形！”你认为小丽的做法有根据吗？命题:两条对角线互相平分的四边形是
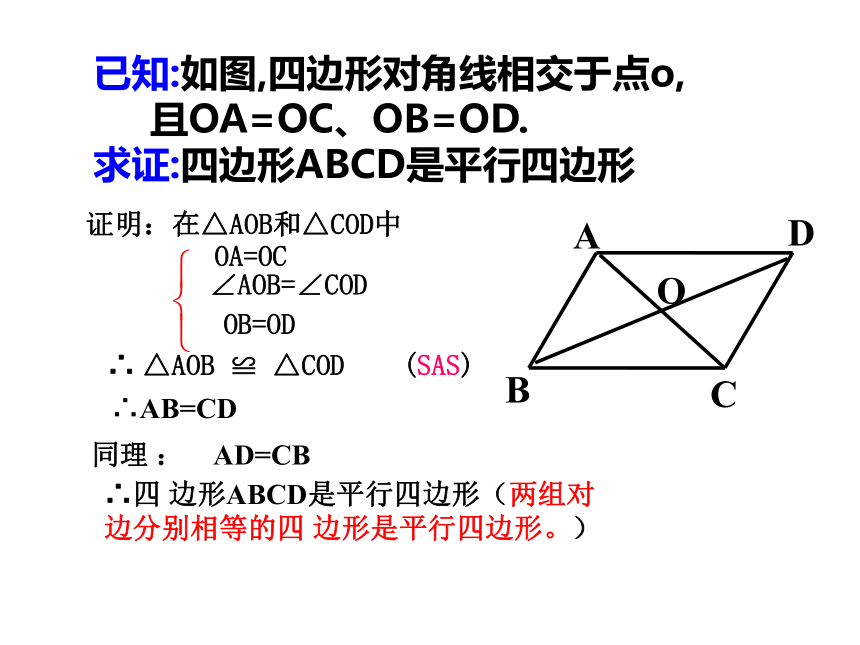
平行四边形.你怎样用理论验证这个猜想呢?已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明：在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 ： AD=CB∴四 边形ABCD是平行四边形（两组对边分别相等的四 边形是平行四边形。）
在四边形ABCD中，∵ OA=OC，OB=OD。 ∴ 四边形ABCD是平行四边形对角线互相平分的四边形是平行四边形.平行四边形判定定理3几何语言：定义: 两组对边分别平行的四边形是 平行四边形
定理1: 一组对边平行且相等的四边形 平行四边形
定理2：两组对边分别相等的四边形是平行四边形
定理3：对角线互相平分的四边形是平行四边形
知识梳理判定平行四边形的方法：开心一练: 根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行C热身运动 1、完成课内练习2
2、已知：如图，在 ABCD中，Ｅ，Ｆ是对角线ＢＤ
上的两点，且BＥ＝ＤＦ．
求证：四边形AECF是平行四边形O思考：根据现有条件，说说你准备选用哪种方法证明？
大概的步骤是怎样的？例1：已知如图，E、F是 ABCD的对角线BD上的两点，且∠BAE=∠DCF 求证：四边形AECF是平行四边形。O证明:连结AC,交BD于点OAB∥CD在 ABCD中，
BO=DO，AO=CO∴∠ABE=∠CDF∠ABE=∠CDF
∠BAE=∠CDF
AB=CD∴△ABE≌△CDF∴BE=DF∴BO-BE=DO-DF，即EO=FO∴四边形AECF是平行四边形而AO=COAB=CD在△AEB和△CFD中ABCDEFO变式1（作业题3）已知：如图,在 ABCD中，∠BAD和∠BCD的平分线AF、CE分别与对角线BD相交于点F，E。 求证：四边形AFCE是平行四边形。课内练习3、如图，在 ABCD中，E，F是对角线AC上的两个点；G，H是对角线BD上的两个点，已知AE=CF，DG=BH，
求证：四边形EHFG是平行四边形证明：
在　　ＡＢＣＤ中，
ＯＡ＝ＯＣ，ＯＢ＝ＯＤ
∵ＡＥ＝ＣＦ，ＤＧ＝ＢＨ
∴OA-AE=OC-CF
OB-BH=OD-DG
即ＯＥ＝ＯＦ，ＯＧ＝ＯＨ
∴四边形EHFG是平行四边形作业题2、?如图,?AC?是 ABCD?的一条对角线.?延长?AC?至?F,?反向延长?AC至E,?使AE＝CF.求证:?四边形EBFD是平行四边形.? 课内练习1已知线段a，b，∠α（如图），请用直尺和圆规作一个平行四边形，使它的两条对角线长分别等于线段a，b，两条对角线的夹角等于∠α作业题1：求作一个平行四边形，
使它的两条对角线长AC=4cm.BD=3cm,
两条对角线的一个夹角为600作业题4如图四边形ABCD是不是平行四边形？请给出证明.ABCDxyo-1-111连接对角线ＡＣ
ＢＤ一定过点O，且有
ＯＡ＝ＯＣ，ＯＢ＝ＯＤ∴四边形ＡＢＣＤ是平行四边形 如图，在 ?ABCD中，已知两条对角线相交于
点O，E、F、G、H分别是BO 、DO 、AO 、CO的中点，
以图中的点为顶点，尽可能多地画出平行四边形。画一画ADCBGEHFO5.已知:?如图,? ABCD?的两条对角线相交于点?O,?直线?EF,?GH?过点O,?分别交?AD,?BC,?AB,?CD?于点?E,?F,?G,?H.?求证:四边形GFHE?是平行四边形. 任意画一个三角形和三角形一边上的中线。比较这条中线的二倍与三角形另外两边的和的大小，你发现了什么?再画几个三角形试一试，你发现的规律仍然成立吗?试证明你的发现。发现：三角形一条边上的中线的2倍小于另两条边的和。E已知：如图，AD是⊿ABC的中线，求证：2ADAE,∴AB+AC>2AD,即2AD从边看: 平行四边形的四个判定方法两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形
从对角线看: 两组对角线互相平分 小结走进生活比比谁更聪明！ABC 现有一块等腰直角三角形铁板，要求切
割一次焊接成一个含有45°角的平行四边形
(不能有余料), 请你设计一种方案，并说
明该方案正确的理由.横对斜CABFCABFDCABEABCF