2022-2023学年浙教版八年级数学下下册4.3 中心对称同步练习 (含解析)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学下下册4.3 中心对称同步练习 (含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 346.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 21:24:35 | ||
图片预览



文档简介
浙教版八下 4.3 中心对称
一、选择题(共8小题)
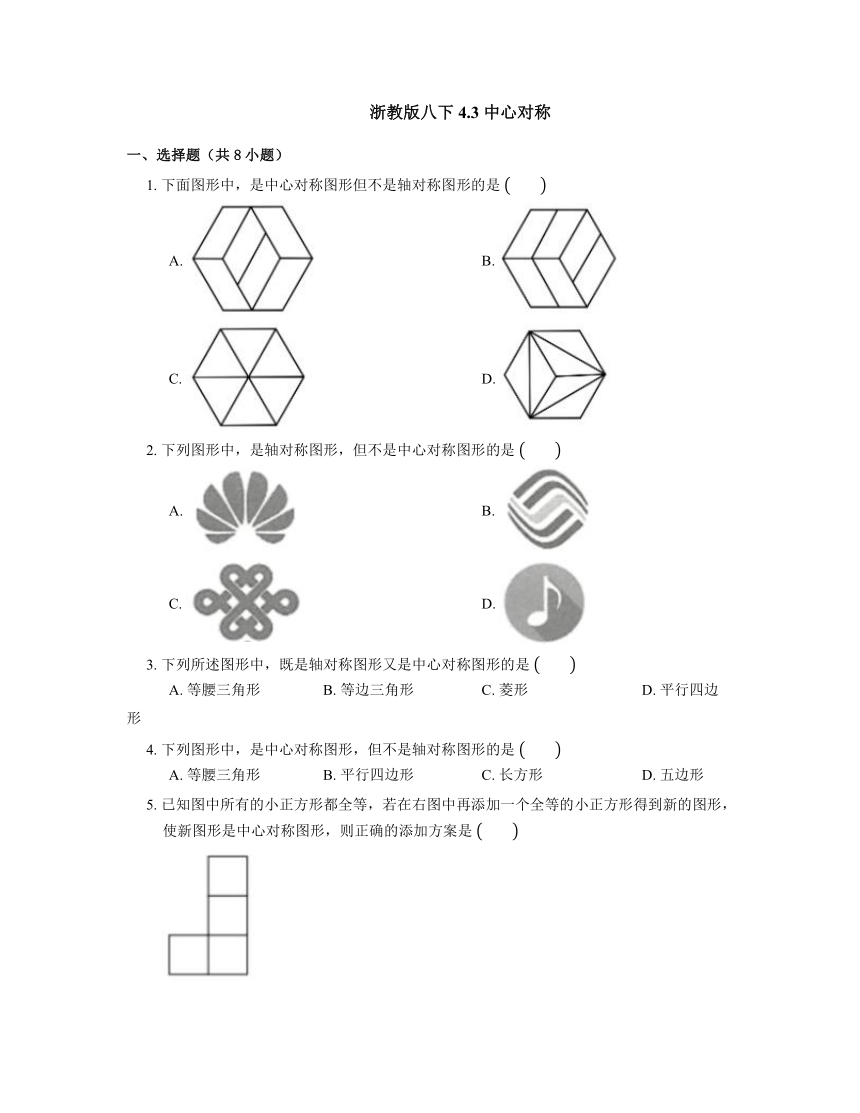
1. 下面图形中,是中心对称图形但不是轴对称图形的是
A. B.
C. D.
2. 下列图形中,是轴对称图形,但不是中心对称图形的是
A. B.
C. D.
3. 下列所述图形中,既是轴对称图形又是中心对称图形的是
A. 等腰三角形 B. 等边三角形 C. 菱形 D. 平行四边形
4. 下列图形中,是中心对称图形,但不是轴对称图形的是
A. 等腰三角形 B. 平行四边形 C. 长方形 D. 五边形
5. 已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是
A. B.
C. D.
6. 下列数学符号中,不是中心对称图形的是
A. B. C. D.
7. 关于中心对称的两个图形的对称中心,下列说法正确的是
A. 两个图形的交点
B. 连接两对对应点,两条线段所在直线的交点
C. 对应角的角平分线交点
D. 两条对应线段所在直线的交点
8. 关于中心对称的两个图形中,下列不相等的量是
A. 对应线段 B. 对应角
C. 对应图形的面积 D. 对称中心到各点的距离
二、填空题(共6小题)
9. 若两个图形成中心对称,分别联结这两个图形的两对对应点,所得两条直线的交点就是 .
10. 平面内,一个图形绕着一个定点旋转 后,能与另一个图形重合,叫做这两个图形 ,也叫做这两个图形 ,这个定点叫做 ,这两个图形中的对应点,也叫做关于这个定点的 .
11. 把一个图形绕着某一点旋转 ,如果它能够与另一个图形重合,那么这两个图形就关于这个点对称,这个点叫做对称中心.对称点的连线段被对称中心 .
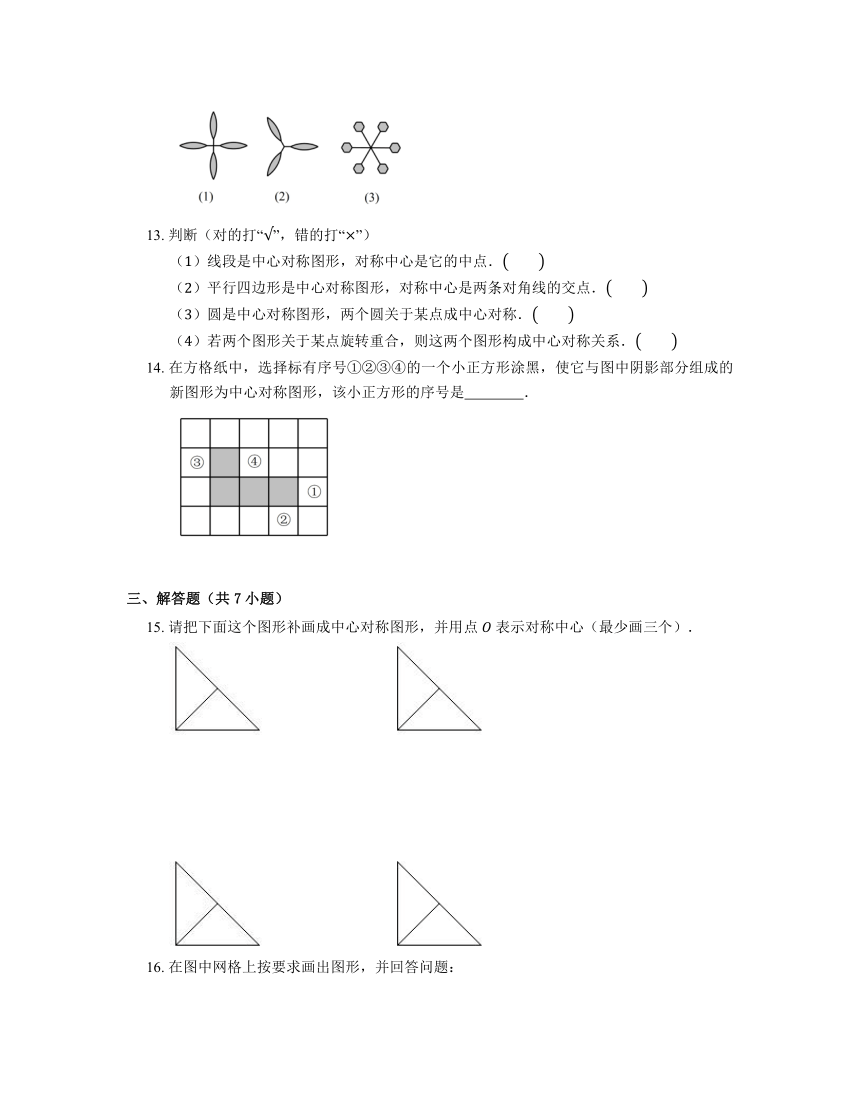
12. 下列图中是中心对称图形的有 .
13. 判断(对的打“”,错的打“”)
()线段是中心对称图形,对称中心是它的中点.
()平行四边形是中心对称图形,对称中心是两条对角线的交点.
()圆是中心对称图形,两个圆关于某点成中心对称.
()若两个图形关于某点旋转重合,则这两个图形构成中心对称关系.
14. 在方格纸中,选择标有序号①②③④的一个小正方形涂黑,使它与图中阴影部分组成的新图形为中心对称图形,该小正方形的序号是 .
三、解答题(共7小题)
15. 请把下面这个图形补画成中心对称图形,并用点 表示对称中心(最少画三个).
16. 在图中网格上按要求画出图形,并回答问题:
(1)先画出 关于直线 的轴对称图形 ,再画出 关于直线 的轴对称图形 .
(2)在()的条件下,请判断 与 的位置关系为 .
17. 如图,画出这个图形关于点 的中心对称的图形.
18. 如图,已知 和点 ,如果 与 关于点 成中心对称,且点 的对应点为点 ,请画出点 和 .
19. 如图,已知两个字母“”成中心对称,请画出它们的对称中心 .
20. 画出半圆关于点 的中心对称的图形.
21. 如图,在 中,点 是边 的中点,画出 关于点 的中心对称的图形.
答案
1. A
【解析】在平面内,把一个图形绕着某个点旋转 ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.轴对称图形的定义为:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.直线叫做对称轴.
根据中心对称图形和轴对称图形的定义可知:
A选项:图形是中心对称图形,不是轴对称图形,符合题意,故A正确;
B选项:图形既不是中心对称图形,也不是轴对称图形,不符合题意,故B错误;
C选项:图形既是中心对称图形,也是轴对称图形,不符合题意,故C错误;
D选项:图形是中心对称图形,不是轴对称图形,不符合题意,故D错误.
2. A
【解析】选项A,是轴对称图形,不是中心对称图形;选项B,只是中心对称图形;选项C,既是轴对称图形,又是中心对称图形;选项D,既不是轴对称图形,又不是中心对称图形.
3. C
【解析】菱形既是轴对称图形,又是中心对称图形.
故选C.
4. B
5. B
【解析】A、新图形不是中心对称图形,故此选项错误;
B、新图形是中心对称图形,故此选项正确;
C、新图形不是中心对称图形,故此选项错误;
D、新图形不是中心对称图形,故此选项错误;
故选:B.
6. D
7. B
8. D
9. 对称中心
10. 关于这个定点对称,成中心对称,对称中心,对称点
11. 平分
12. (1),(3)
13. ,,,
14. ②
15.
16. (1) 图略
(2) 关于点 成中心对称
17.
所以此图为所求.
18.
所以点 为对称中心, 为所求三角形.
19.
所以点 为对称中心.
20.
所以此图为所求.
21.
所以 为所求作三角形.
一、选择题(共8小题)
1. 下面图形中,是中心对称图形但不是轴对称图形的是
A. B.
C. D.
2. 下列图形中,是轴对称图形,但不是中心对称图形的是
A. B.
C. D.
3. 下列所述图形中,既是轴对称图形又是中心对称图形的是
A. 等腰三角形 B. 等边三角形 C. 菱形 D. 平行四边形
4. 下列图形中,是中心对称图形,但不是轴对称图形的是
A. 等腰三角形 B. 平行四边形 C. 长方形 D. 五边形
5. 已知图中所有的小正方形都全等,若在右图中再添加一个全等的小正方形得到新的图形,使新图形是中心对称图形,则正确的添加方案是
A. B.
C. D.
6. 下列数学符号中,不是中心对称图形的是
A. B. C. D.
7. 关于中心对称的两个图形的对称中心,下列说法正确的是
A. 两个图形的交点
B. 连接两对对应点,两条线段所在直线的交点
C. 对应角的角平分线交点
D. 两条对应线段所在直线的交点
8. 关于中心对称的两个图形中,下列不相等的量是
A. 对应线段 B. 对应角
C. 对应图形的面积 D. 对称中心到各点的距离
二、填空题(共6小题)
9. 若两个图形成中心对称,分别联结这两个图形的两对对应点,所得两条直线的交点就是 .
10. 平面内,一个图形绕着一个定点旋转 后,能与另一个图形重合,叫做这两个图形 ,也叫做这两个图形 ,这个定点叫做 ,这两个图形中的对应点,也叫做关于这个定点的 .
11. 把一个图形绕着某一点旋转 ,如果它能够与另一个图形重合,那么这两个图形就关于这个点对称,这个点叫做对称中心.对称点的连线段被对称中心 .
12. 下列图中是中心对称图形的有 .
13. 判断(对的打“”,错的打“”)
()线段是中心对称图形,对称中心是它的中点.
()平行四边形是中心对称图形,对称中心是两条对角线的交点.
()圆是中心对称图形,两个圆关于某点成中心对称.
()若两个图形关于某点旋转重合,则这两个图形构成中心对称关系.
14. 在方格纸中,选择标有序号①②③④的一个小正方形涂黑,使它与图中阴影部分组成的新图形为中心对称图形,该小正方形的序号是 .
三、解答题(共7小题)
15. 请把下面这个图形补画成中心对称图形,并用点 表示对称中心(最少画三个).
16. 在图中网格上按要求画出图形,并回答问题:
(1)先画出 关于直线 的轴对称图形 ,再画出 关于直线 的轴对称图形 .
(2)在()的条件下,请判断 与 的位置关系为 .
17. 如图,画出这个图形关于点 的中心对称的图形.
18. 如图,已知 和点 ,如果 与 关于点 成中心对称,且点 的对应点为点 ,请画出点 和 .
19. 如图,已知两个字母“”成中心对称,请画出它们的对称中心 .
20. 画出半圆关于点 的中心对称的图形.
21. 如图,在 中,点 是边 的中点,画出 关于点 的中心对称的图形.
答案
1. A
【解析】在平面内,把一个图形绕着某个点旋转 ,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形.轴对称图形的定义为:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.直线叫做对称轴.
根据中心对称图形和轴对称图形的定义可知:
A选项:图形是中心对称图形,不是轴对称图形,符合题意,故A正确;
B选项:图形既不是中心对称图形,也不是轴对称图形,不符合题意,故B错误;
C选项:图形既是中心对称图形,也是轴对称图形,不符合题意,故C错误;
D选项:图形是中心对称图形,不是轴对称图形,不符合题意,故D错误.
2. A
【解析】选项A,是轴对称图形,不是中心对称图形;选项B,只是中心对称图形;选项C,既是轴对称图形,又是中心对称图形;选项D,既不是轴对称图形,又不是中心对称图形.
3. C
【解析】菱形既是轴对称图形,又是中心对称图形.
故选C.
4. B
5. B
【解析】A、新图形不是中心对称图形,故此选项错误;
B、新图形是中心对称图形,故此选项正确;
C、新图形不是中心对称图形,故此选项错误;
D、新图形不是中心对称图形,故此选项错误;
故选:B.
6. D
7. B
8. D
9. 对称中心
10. 关于这个定点对称,成中心对称,对称中心,对称点
11. 平分
12. (1),(3)
13. ,,,
14. ②
15.
16. (1) 图略
(2) 关于点 成中心对称
17.
所以此图为所求.
18.
所以点 为对称中心, 为所求三角形.
19.
所以点 为对称中心.
20.
所以此图为所求.
21.
所以 为所求作三角形.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
