2022-2023学年浙教版八年级数学下册4.4 平行四边形的判定定理同步练习 (含解析)
文档属性
| 名称 | 2022-2023学年浙教版八年级数学下册4.4 平行四边形的判定定理同步练习 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 342.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 00:00:00 | ||
图片预览


文档简介
浙教版八下 4.4 平行四边形的判定定理
一、选择题(共13小题)
1. 已知 ,,则四边形 是
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
2. 如图, 是面积为 的平行四边 内任意一点, 的面积为 , 的面积为 ,则
A. B.
C. D. 的大小与 点位置有关
3. 如图,已知直线 , 被直线 所截,,,则 的度数为
A. B. C. D.
4. 下面给出了四边形 中,,,, 的度数之比,其中能判定四边形 是平行四边形的是
A. B. C. D.
5. 下列说法错误的是
A. 对角线互相平分的四边形是平行四边形
B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边相等,另一组对边平行的四边形是平行四边形
6. 如图,平行四边形 中,, 分别为 , 边上的一点,增加下列条件,不能得出 的是
A. B.
C. D.
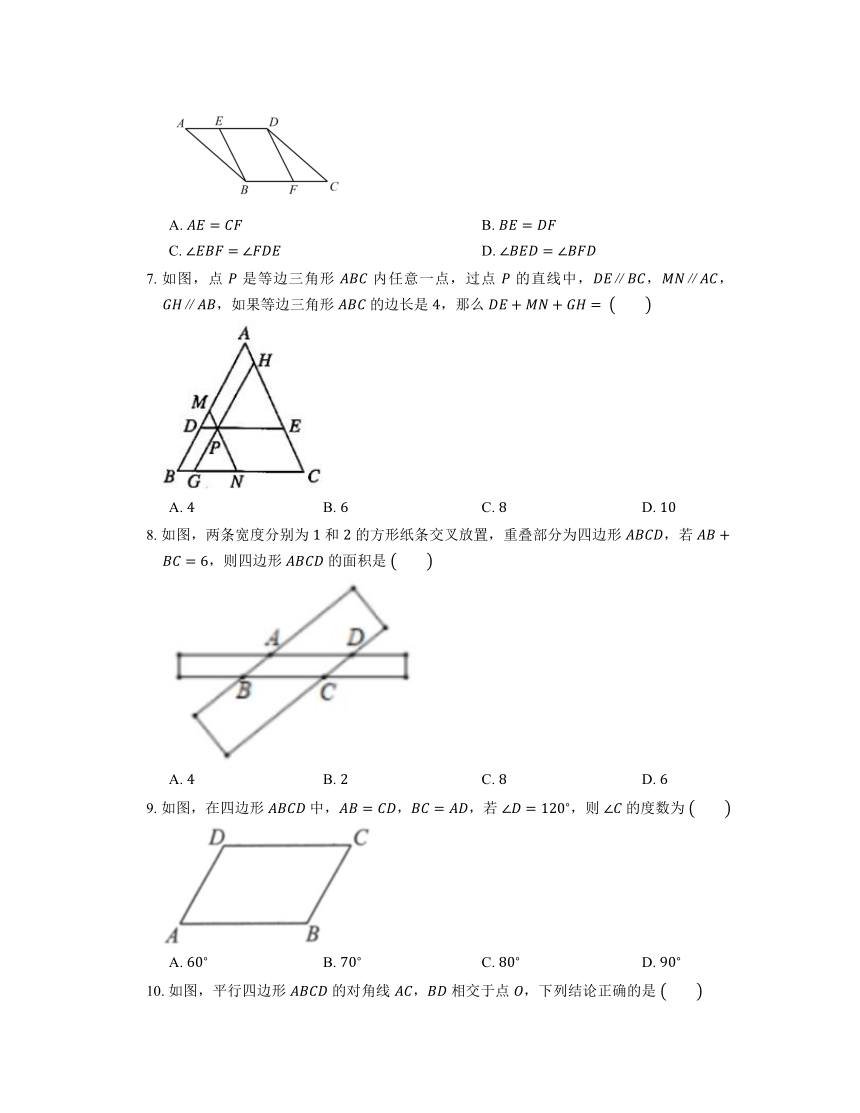
7. 如图,点 是等边三角形 内任意一点,过点 的直线中,,,,如果等边三角形 的边长是 ,那么
A. B. C. D.
8. 如图,两条宽度分别为 和 的方形纸条交叉放置,重叠部分为四边形 ,若 ,则四边形 的面积是
A. B. C. D.
9. 如图,在四边形 中,,,若 ,则 的度数为
A. B. C. D.
10. 如图,平行四边形 的对角线 , 相交于点 ,下列结论正确的是
A.
B.
C.
D. 平行四边形 是轴对称图形
11. 下列命题是假命题的是
A. 斜边和一条直角边分别相等的两个直角三角形全等
B. 等腰三角形的一边长为 ,另一边长为 ,则这个三角形的周长为
C. 若代数式 有意义,则 的取值范围是
D. 两组对边分别平行的四边形是平行四边形
12. 如图,在四边形 中,,要使四边形 是平行四边形,下列添加的条件不确定的是
A. B. C. D.
13. 如图,在矩形 中,,,点 在边上以每秒 的速度从点 向点 运动,点 在 边上,以每秒 的速度从点 出发,在 间往返运动,两个点同时出发,当点 到达点 时停止(同时点 也停止),在这段时间内,线段 平行于 的次数是
A. B. C. D.
二、填空题(共7小题)
14. 如图,点 是直线 外一点,在 上取两点 ,,连接 ,分别以点 , 为圆心,, 的长为半径画弧,两弧交于点 ,连接 ,,则四边形 是平行四边形,理由是 .
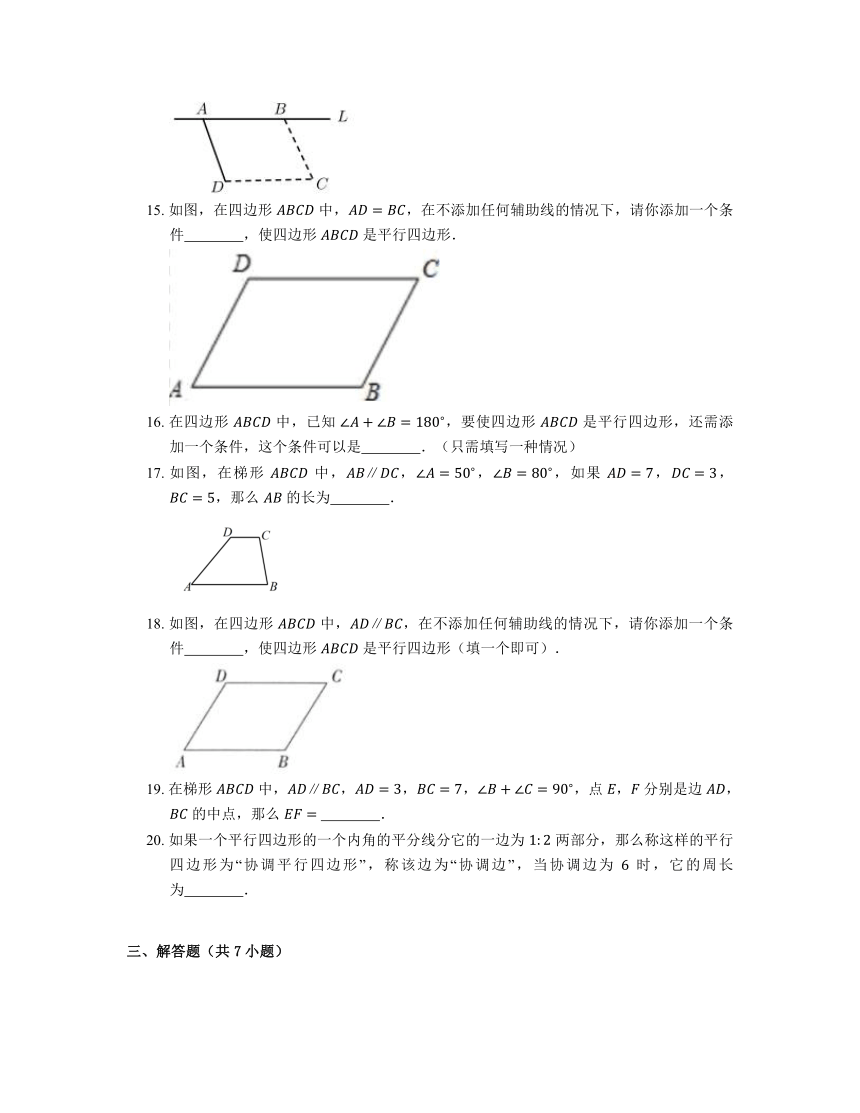
15. 如图,在四边形 中,,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形 是平行四边形.
16. 在四边形 中,已知 ,要使四边形 是平行四边形,还需添加一个条件,这个条件可以是 .(只需填写一种情况)
17. 如图,在梯形 中,,,,如果 ,,,那么 的长为 .
18. 如图,在四边形 中,,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形 是平行四边形(填一个即可).
19. 在梯形 中,,,,,点 , 分别是边 , 的中点,那么 .
20. 如果一个平行四边形的一个内角的平分线分它的一边为 两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”,当协调边为 时,它的周长为 .
三、解答题(共7小题)
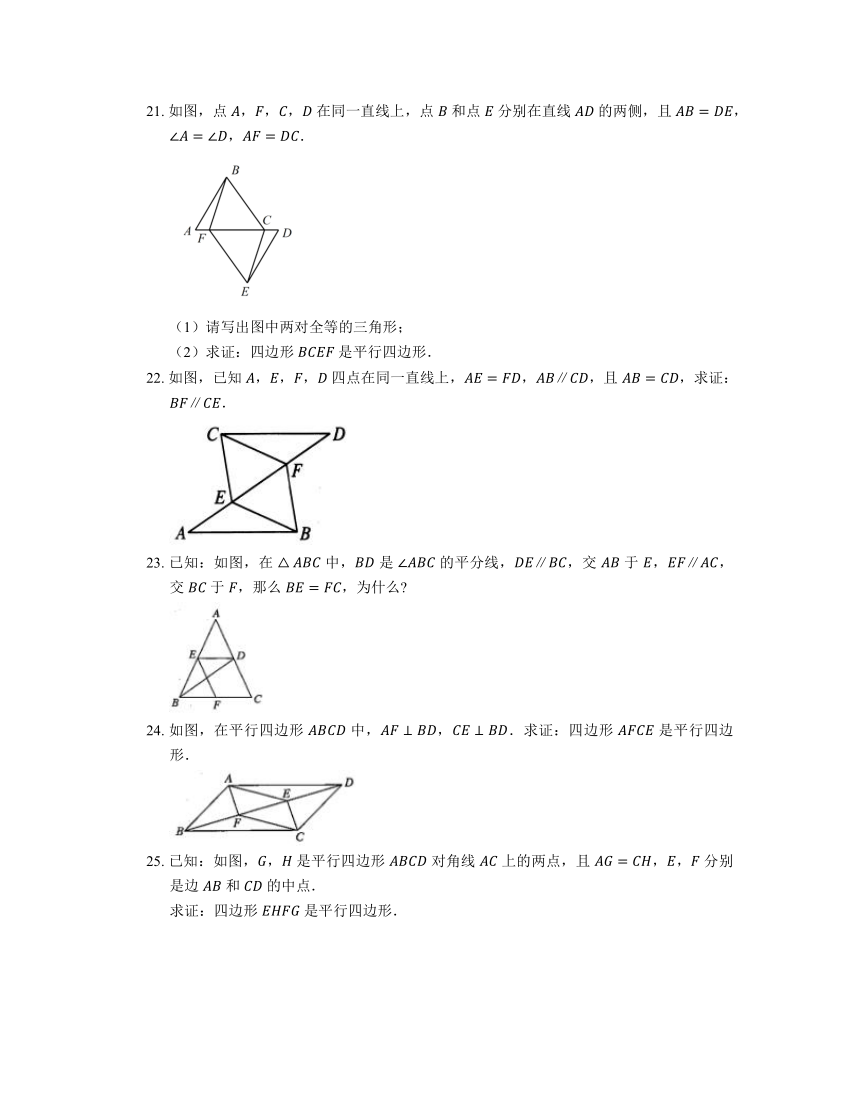
21. 如图,点 ,,, 在同一直线上,点 和点 分别在直线 的两侧,且 ,,.
(1)请写出图中两对全等的三角形;
(2)求证:四边形 是平行四边形.
22. 如图,已知 ,,, 四点在同一直线上,,,且 ,求证:.
23. 已知:如图,在 中, 是 的平分线,,交 于 ,,交 于 ,那么 ,为什么
24. 如图,在平行四边形 中,,.求证:四边形 是平行四边形.
25. 已知:如图,, 是平行四边形 对角线 上的两点,且 ,, 分别是边 和 的中点.
求证:四边形 是平行四边形.
26. 如图,已知四边形 是平行四边形, 于点 , 于点 ,延长 , 分别交 , 于点 ,.
(1)求证:四边形 是平行四边形;
(2)已知 ,,求 的长.
27. 如图,在平面直角坐标系中,,,,,并且 , 满足 .一动点 从点 出发,在线段 上以每秒 个单位长度的速度向点 运动;动点 从点 出发在线段 上以每秒 个单位长度的速度向点 运动,点 , 分别从点 , 同时出发,当点 运动到点 时,点 随之停止运动.设运动时间为 (秒).
(1)求 , 两点的坐标;
(2)当 为何值时,四边形 是平行四边形 并求出此 时 , 两点的坐标;
(3)当 为何值时, 是以 为腰的等腰三角形 并求出 , 两点的坐标.
答案
1. A
2. C
3. C
4. B
5. D
6. B
【解析】 四边形 是平行四边形,
,,
A、 ,
,
四边形 是平行四边形,
,故本选项能判定 ;
B、 ,
四边形 是平行四边形或等腰梯形,
故本选项不能判定 ;
C、 ,
,,
,
,
四边形 是平行四边形,
,故本选项能判定 ;
D、 ,
,,
,
,
四边形 是平行四边形,
,故本选项能判定 .
7. C
8. A
【解析】依题意得:,,则四边形 是平行四边形.
如图,过点 作 于点 ,过点 作 于点 .
,,
,
.
又 ,
,.
四边形 的面积 .
9. A
10. A
11. B
12. A
【解析】A.当 , 时,四边形 可能为等腰梯形,所以不能证明四边形 为平行四边形,符合题意;
B.,,一组对边平行且相等,可证明四边形 为平行四边形,不符合题意;
C.,,两组对边分别平行,可证明四边形 为平行四边形,不符合题意;
D.因为 ,所以 ,因为 ,所以 ,所以 ,所以四边形 为平行四边形,不符合题意.
故选A.
13. C 【解析】当 时,.
,,
四边形 为平行四边形,
.
点 运动的时间 秒,
点 运动的路程 .
点 可在 间往返 次.
在这段时间内 与 有 次平行.
故选:C.
14. 两组对边分别相等的四边形是平行四边形
【解析】根据尺规作图的画法可得,,,
四边形 是平行四边形.
15. ()
16. 答案不唯一,如 等.
17.
18. (答案不唯一)
【解析】根据平行四边形的判定定理,可以添加的一个条件是 .
故可以填 (答案不唯一).
19.
【解析】过点 作 ,,
,
四边形 , 均为平行四边形,
,,
,,
,,
又 ,
,
,
点 , 分别是边 , 的中点,
,,
,,
.
20. 或
【解析】如图所示:
①当 , 时,
四边形 是平行四边形,
,,,
,
平分 ,
,
,
,
平行四边形 的周长 ;
②当 , 时,同理得:,
平行四边形 的周长 .
21. (1) ,.
(2) ,
,
又 ,
,
四边形 是平行四边形.
22. 证 .
23. 用定义说明四边形 为平行四边形,得到 ,再证 ,从而得 .
24. 先证 ,再证 ,得到 .
25. 先运用平行四边形的性质证明 ,得 且 ,再由一组对边平行且相等推出四边形 是平行四边形.
26. (1) 四边形 是平行四边形,
,
,,
,
四边形 是平行四边形.
(2) 四边形 是平行四边形,
,
,
,
,
,
,
,
,
在 中,.
27. (1) 因为 ,
所以 ,,
故 ,.
(2) 根据题意得:,,
则:,,
因为当 时,四边形 是平行四边形,
所以 ,
计算得出:,
所以 ,.
(3) 当 时,过 作 ,如图所示,
根据题意得:,
计算得出:,
故 ,,
当 时,过 作 轴,如图所示,
根据题意得:,,
则 ,
计算得出:,,
故 ,.
一、选择题(共13小题)
1. 已知 ,,则四边形 是
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
2. 如图, 是面积为 的平行四边 内任意一点, 的面积为 , 的面积为 ,则
A. B.
C. D. 的大小与 点位置有关
3. 如图,已知直线 , 被直线 所截,,,则 的度数为
A. B. C. D.
4. 下面给出了四边形 中,,,, 的度数之比,其中能判定四边形 是平行四边形的是
A. B. C. D.
5. 下列说法错误的是
A. 对角线互相平分的四边形是平行四边形
B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边相等,另一组对边平行的四边形是平行四边形
6. 如图,平行四边形 中,, 分别为 , 边上的一点,增加下列条件,不能得出 的是
A. B.
C. D.
7. 如图,点 是等边三角形 内任意一点,过点 的直线中,,,,如果等边三角形 的边长是 ,那么
A. B. C. D.
8. 如图,两条宽度分别为 和 的方形纸条交叉放置,重叠部分为四边形 ,若 ,则四边形 的面积是
A. B. C. D.
9. 如图,在四边形 中,,,若 ,则 的度数为
A. B. C. D.
10. 如图,平行四边形 的对角线 , 相交于点 ,下列结论正确的是
A.
B.
C.
D. 平行四边形 是轴对称图形
11. 下列命题是假命题的是
A. 斜边和一条直角边分别相等的两个直角三角形全等
B. 等腰三角形的一边长为 ,另一边长为 ,则这个三角形的周长为
C. 若代数式 有意义,则 的取值范围是
D. 两组对边分别平行的四边形是平行四边形
12. 如图,在四边形 中,,要使四边形 是平行四边形,下列添加的条件不确定的是
A. B. C. D.
13. 如图,在矩形 中,,,点 在边上以每秒 的速度从点 向点 运动,点 在 边上,以每秒 的速度从点 出发,在 间往返运动,两个点同时出发,当点 到达点 时停止(同时点 也停止),在这段时间内,线段 平行于 的次数是
A. B. C. D.
二、填空题(共7小题)
14. 如图,点 是直线 外一点,在 上取两点 ,,连接 ,分别以点 , 为圆心,, 的长为半径画弧,两弧交于点 ,连接 ,,则四边形 是平行四边形,理由是 .
15. 如图,在四边形 中,,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形 是平行四边形.
16. 在四边形 中,已知 ,要使四边形 是平行四边形,还需添加一个条件,这个条件可以是 .(只需填写一种情况)
17. 如图,在梯形 中,,,,如果 ,,,那么 的长为 .
18. 如图,在四边形 中,,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形 是平行四边形(填一个即可).
19. 在梯形 中,,,,,点 , 分别是边 , 的中点,那么 .
20. 如果一个平行四边形的一个内角的平分线分它的一边为 两部分,那么称这样的平行四边形为“协调平行四边形”,称该边为“协调边”,当协调边为 时,它的周长为 .
三、解答题(共7小题)
21. 如图,点 ,,, 在同一直线上,点 和点 分别在直线 的两侧,且 ,,.
(1)请写出图中两对全等的三角形;
(2)求证:四边形 是平行四边形.
22. 如图,已知 ,,, 四点在同一直线上,,,且 ,求证:.
23. 已知:如图,在 中, 是 的平分线,,交 于 ,,交 于 ,那么 ,为什么
24. 如图,在平行四边形 中,,.求证:四边形 是平行四边形.
25. 已知:如图,, 是平行四边形 对角线 上的两点,且 ,, 分别是边 和 的中点.
求证:四边形 是平行四边形.
26. 如图,已知四边形 是平行四边形, 于点 , 于点 ,延长 , 分别交 , 于点 ,.
(1)求证:四边形 是平行四边形;
(2)已知 ,,求 的长.
27. 如图,在平面直角坐标系中,,,,,并且 , 满足 .一动点 从点 出发,在线段 上以每秒 个单位长度的速度向点 运动;动点 从点 出发在线段 上以每秒 个单位长度的速度向点 运动,点 , 分别从点 , 同时出发,当点 运动到点 时,点 随之停止运动.设运动时间为 (秒).
(1)求 , 两点的坐标;
(2)当 为何值时,四边形 是平行四边形 并求出此 时 , 两点的坐标;
(3)当 为何值时, 是以 为腰的等腰三角形 并求出 , 两点的坐标.
答案
1. A
2. C
3. C
4. B
5. D
6. B
【解析】 四边形 是平行四边形,
,,
A、 ,
,
四边形 是平行四边形,
,故本选项能判定 ;
B、 ,
四边形 是平行四边形或等腰梯形,
故本选项不能判定 ;
C、 ,
,,
,
,
四边形 是平行四边形,
,故本选项能判定 ;
D、 ,
,,
,
,
四边形 是平行四边形,
,故本选项能判定 .
7. C
8. A
【解析】依题意得:,,则四边形 是平行四边形.
如图,过点 作 于点 ,过点 作 于点 .
,,
,
.
又 ,
,.
四边形 的面积 .
9. A
10. A
11. B
12. A
【解析】A.当 , 时,四边形 可能为等腰梯形,所以不能证明四边形 为平行四边形,符合题意;
B.,,一组对边平行且相等,可证明四边形 为平行四边形,不符合题意;
C.,,两组对边分别平行,可证明四边形 为平行四边形,不符合题意;
D.因为 ,所以 ,因为 ,所以 ,所以 ,所以四边形 为平行四边形,不符合题意.
故选A.
13. C 【解析】当 时,.
,,
四边形 为平行四边形,
.
点 运动的时间 秒,
点 运动的路程 .
点 可在 间往返 次.
在这段时间内 与 有 次平行.
故选:C.
14. 两组对边分别相等的四边形是平行四边形
【解析】根据尺规作图的画法可得,,,
四边形 是平行四边形.
15. ()
16. 答案不唯一,如 等.
17.
18. (答案不唯一)
【解析】根据平行四边形的判定定理,可以添加的一个条件是 .
故可以填 (答案不唯一).
19.
【解析】过点 作 ,,
,
四边形 , 均为平行四边形,
,,
,,
,,
又 ,
,
,
点 , 分别是边 , 的中点,
,,
,,
.
20. 或
【解析】如图所示:
①当 , 时,
四边形 是平行四边形,
,,,
,
平分 ,
,
,
,
平行四边形 的周长 ;
②当 , 时,同理得:,
平行四边形 的周长 .
21. (1) ,.
(2) ,
,
又 ,
,
四边形 是平行四边形.
22. 证 .
23. 用定义说明四边形 为平行四边形,得到 ,再证 ,从而得 .
24. 先证 ,再证 ,得到 .
25. 先运用平行四边形的性质证明 ,得 且 ,再由一组对边平行且相等推出四边形 是平行四边形.
26. (1) 四边形 是平行四边形,
,
,,
,
四边形 是平行四边形.
(2) 四边形 是平行四边形,
,
,
,
,
,
,
,
,
在 中,.
27. (1) 因为 ,
所以 ,,
故 ,.
(2) 根据题意得:,,
则:,,
因为当 时,四边形 是平行四边形,
所以 ,
计算得出:,
所以 ,.
(3) 当 时,过 作 ,如图所示,
根据题意得:,
计算得出:,
故 ,,
当 时,过 作 轴,如图所示,
根据题意得:,,
则 ,
计算得出:,,
故 ,.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
