2.7 探索勾股定理同步练习(含解析)
文档属性
| 名称 | 2.7 探索勾股定理同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 251.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 10:40:16 | ||
图片预览


文档简介
2.7探索勾股定理 同步练习
一.选择题(共8小题)
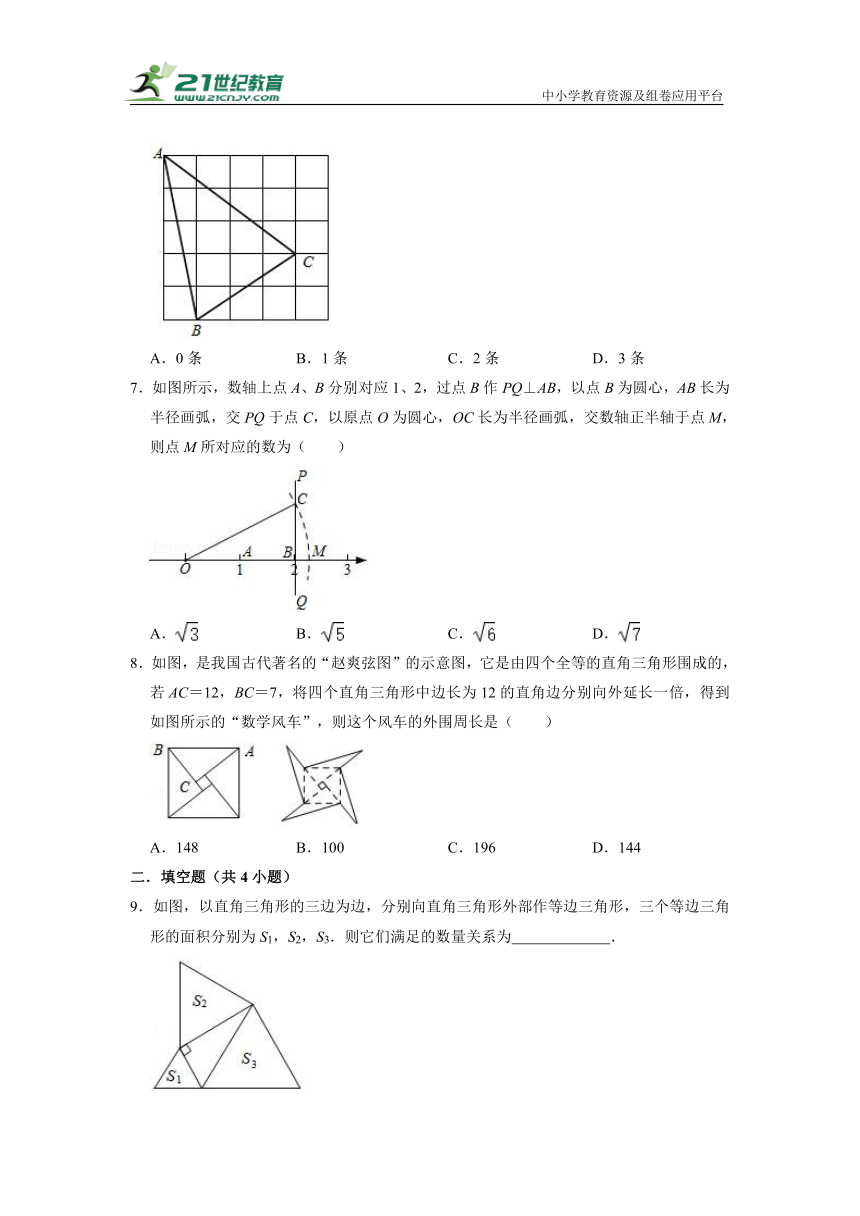
1.如图,在△ABC中,∠C=90°,AB+BC=8,AC=4,则△ABC的面积为( )
A.6 B.7.5 C.10 D.12
2.已知直角三角形的斜边长为15,一直角边长为12,则另一条直角边长为( )
A. B.3 C.27 D.9
3.三个正方形的面积如图所示,则S的值为( )
A.3 B.12 C.9 D.4
4.若直角三角形的两条边长分别为a、b,且满足a=3,b=4,则该直角三角形的第三边的长为( )
A.5 B. C.5或 D.不确定
5.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
6.如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点A,B,C均在网格的格点上,则△ABC的三条边中边长是无理数的有( )
A.0条 B.1条 C.2条 D.3条
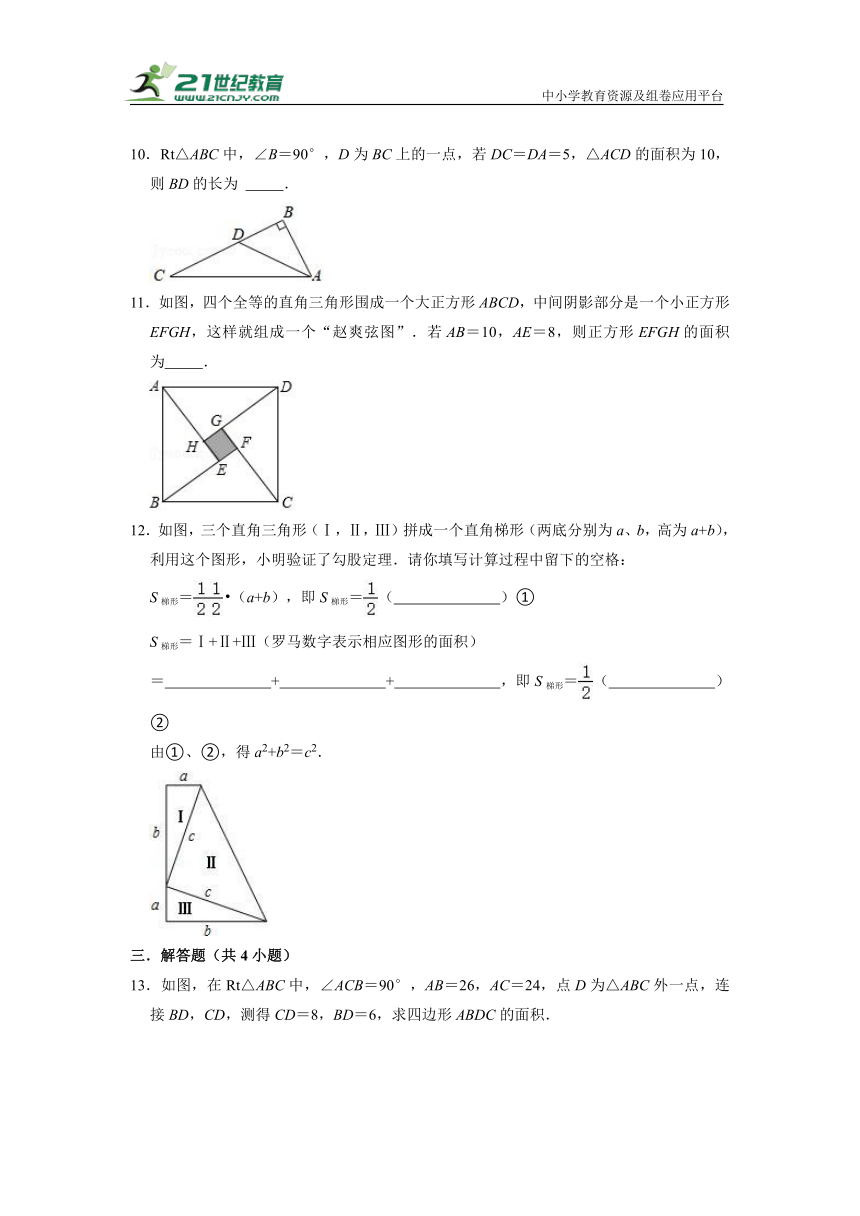
7.如图所示,数轴上点A、B分别对应1、2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴正半轴于点M,则点M所对应的数为( )
A. B. C. D.
8.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是( )
A.148 B.100 C.196 D.144
二.填空题(共4小题)
9.如图,以直角三角形的三边为边,分别向直角三角形外部作等边三角形,三个等边三角形的面积分别为S1,S2,S3.则它们满足的数量关系为 .
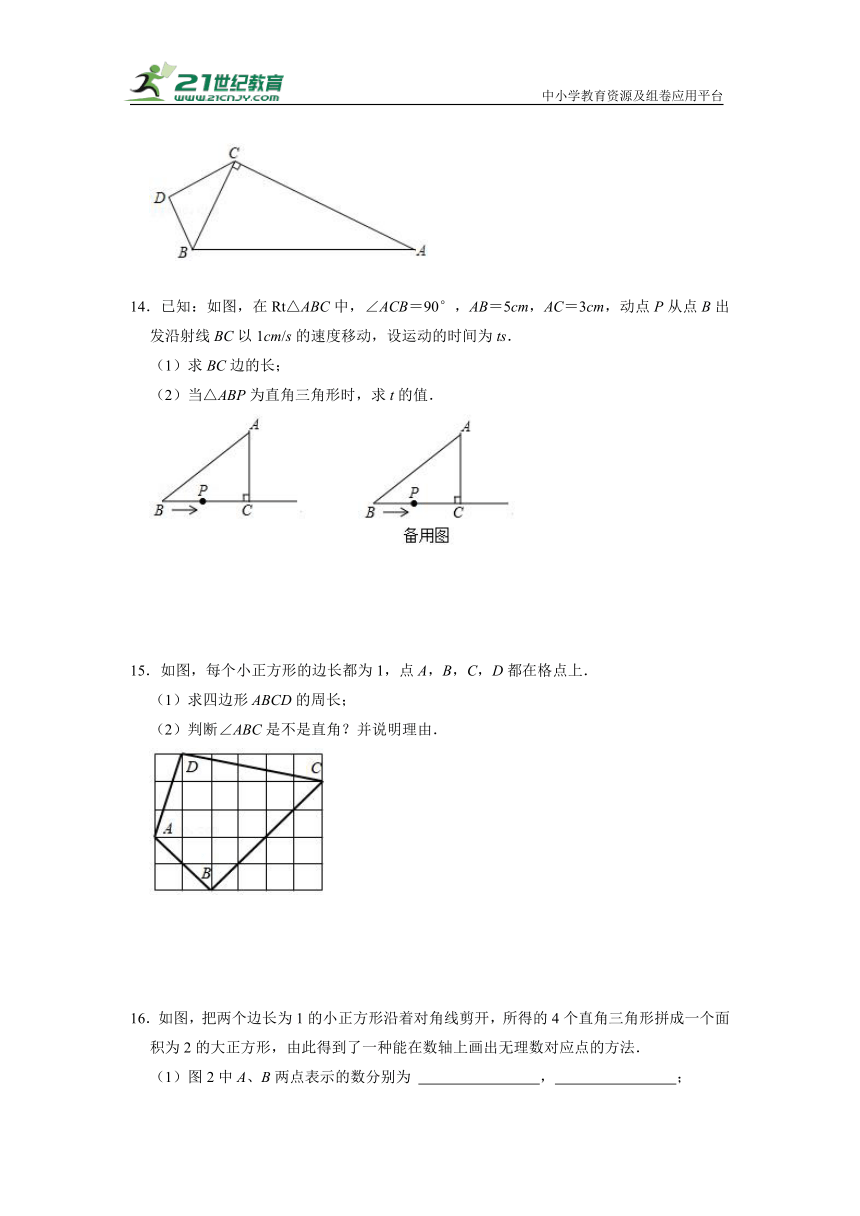
10.Rt△ABC中,∠B=90°,D为BC上的一点,若DC=DA=5,△ACD的面积为10,则BD的长为 .
11.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影部分是一个小正方形EFGH,这样就组成一个“赵爽弦图”.若AB=10,AE=8,则正方形EFGH的面积为 .
12.如图,三个直角三角形(Ⅰ,Ⅱ,Ⅲ)拼成一个直角梯形(两底分别为a、b,高为a+b),利用这个图形,小明验证了勾股定理.请你填写计算过程中留下的空格:
S梯形= (a+b),即S梯形=( )①
S梯形=Ⅰ+Ⅱ+Ⅲ(罗马数字表示相应图形的面积)
= + + ,即S梯形=( )②
由①、②,得a2+b2=c2.
三.解答题(共4小题)
13.如图,在Rt△ABC中,∠ACB=90°,AB=26,AC=24,点D为△ABC外一点,连接BD,CD,测得CD=8,BD=6,求四边形ABDC的面积.
14.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
15.如图,每个小正方形的边长都为1,点A,B,C,D都在格点上.
(1)求四边形ABCD的周长;
(2)判断∠ABC是不是直角?并说明理由.
16.如图,把两个边长为1的小正方形沿着对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形,由此得到了一种能在数轴上画出无理数对应点的方法.
(1)图2中A、B两点表示的数分别为 , ;
(2)请你参考以上方法:
①把图3中5×1的长方形进行剪裁,并拼成一个大正方形,在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a= .(注:小正方形边长都是1,拼接不重叠也无空隙)
②在①的基础上,参考图2的画法,在数轴上用M表示数a,图中标出必要线段长.
2.7探索勾股定理 同步练习
参考答案与试题解析
一.选择题(共8小题)
1.如图,在△ABC中,∠C=90°,AB+BC=8,AC=4,则△ABC的面积为( )
A.6 B.7.5 C.10 D.12
解:设BC=x,
∵AB+BC=8,
∴AB=8﹣x,
在Rt△ABC中,∠C=90°,
∴AB2=BC2+AC2,
∴x2+42=(8﹣x)2,
∴x=3,
∴BC=3,
∴S===6,
即△ABC的面积为6,
故选:A.
2.已知直角三角形的斜边长为15,一直角边长为12,则另一条直角边长为( )
A. B.3 C.27 D.9
解:∵直角三角形的斜边长为15,一直角边长为12,
∴另一条直角边长=,
故选:D.
3.三个正方形的面积如图所示,则S的值为( )
A.3 B.12 C.9 D.4
解:如图,
由题意可得:AB=4,AC=5,
∵AC2=AB2+BC2,
∴BC2=25﹣16=9,
∴S=9,
故选:C.
4.若直角三角形的两条边长分别为a、b,且满足a=3,b=4,则该直角三角形的第三边的长为( )
A.5 B. C.5或 D.不确定
解:①当a,b为两直角边时,根据勾股定理,
第三边长为:==5,
且3+4>5,
②当b为斜边长时,根据勾股定理,
第三边长为:=,
且3+>4,
∴该直角三角形的第三边的长为5或,
故选:C.
5.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
解:A、∵ab+c2+ab=(a+b)(a+b),
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
B、∵4×ab+c2=(a+b)2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
C、∵4×ab+(b﹣a)2=c2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
D、根据图形不能证明勾股定理,故本选项符合题意;
故选:D.
6.如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点A,B,C均在网格的格点上,则△ABC的三条边中边长是无理数的有( )
A.0条 B.1条 C.2条 D.3条
解:由勾股定理得:AB=,是无理数;
BC=,是无理数;
AC=,是有理数.
∴△ABC的三条边中边长是无理数的有2条,
故选:C.
7.如图所示,数轴上点A、B分别对应1、2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴正半轴于点M,则点M所对应的数为( )
A. B. C. D.
解:∵OA=1,OB=2,
∴AB=1,
由作图可知:OB=2,BC=AB=1,∠OBC=90°,
∴OM=OC=,
∴点M所对应的数为,
故选:B.
8.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是( )
A.148 B.100 C.196 D.144
解:设将CA延长到点D,连接BD,
根据题意,得CD=12×2=24,BC=7,
∵∠BCD=90°,
∴BC2+CD2=BD2,即72+242=BD2,
∴BD=25,
∴AD+BD=12+25=37,
∴这个风车的外围周长是37×4=148.
故选:A.
二.填空题(共4小题)
9.如图,以直角三角形的三边为边,分别向直角三角形外部作等边三角形,三个等边三角形的面积分别为S1,S2,S3.则它们满足的数量关系为 S1+S2=S3 .
解:设AC=a,BC=b,AB=c,
∵△ABC是直角三角形,
∴a2+b2=c2,
∴a2+b2=c2,
又∵S1=×sin60°a a=a2,S2=b2,S3=c2,
∴S1+S2=S3,
故答案是:S1+S2=S3.
10.Rt△ABC中,∠B=90°,D为BC上的一点,若DC=DA=5,△ACD的面积为10,则BD的长为 3 .
解:设BD=x,
在Rt△ABD中,由勾股定理得:AB==,
∵△ACD的面积为10,
∴×DC×AB=10,即×5×=10,
解得:x1=3,x2=﹣3(舍去),
∴BD的长为3,
故答案为:3.
11.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影部分是一个小正方形EFGH,这样就组成一个“赵爽弦图”.若AB=10,AE=8,则正方形EFGH的面积为 4 .
解:直角三角形直角边的较短边为=6,
正方形EFGH的面积=10×10﹣8×6÷2×4=100﹣96=4.
故答案为:4.
12.如图,三个直角三角形(Ⅰ,Ⅱ,Ⅲ)拼成一个直角梯形(两底分别为a、b,高为a+b),利用这个图形,小明验证了勾股定理.请你填写计算过程中留下的空格:
S梯形= (a+b),即S梯形=( a2+2ab+b2 )①
S梯形=Ⅰ+Ⅱ+Ⅲ(罗马数字表示相应图形的面积)
= ab + c2 + ab ,即S梯形=( 2ab+c2 )②
由①、②,得a2+b2=c2.
解:因为,
又因为S梯形=Ⅰ+Ⅱ+Ⅲ=ab+c2+ab=,
所以=,
得c2=a2+b2.
故答案为:a2+2ab+b2,ab,c2,ab,2ab+c2.
三.解答题(共4小题)
13.如图,在Rt△ABC中,∠ACB=90°,AB=26,AC=24,点D为△ABC外一点,连接BD,CD,测得CD=8,BD=6,求四边形ABDC的面积.
解:在Rt△ABC中,∠ACB=90°,
由勾股定理得:BC=,
∵CD=8,BD=6,
∴CD2+BD2=82+62=100,
AC2=100,
∴CD2+BD2=AC2,
∴∠D=90°,
∴S四边形ABDC=S△ABC+S△BCD
=
=
=144.
14.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
解:(1)在Rt△ABC中,由勾股定理得:BC===4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
15.如图,每个小正方形的边长都为1,点A,B,C,D都在格点上.
(1)求四边形ABCD的周长;
(2)判断∠ABC是不是直角?并说明理由.
解:(1)由勾股定理可得:AB=,BC=,
CD=,AD=,
∴四边形ABCD的周长=2,
(2)∠ABC是直角,理由如下:
连接AC,由勾股定理可得:AC=,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
∴∠ABC是直角.
26.如图,把两个边长为1的小正方形沿着对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形,由此得到了一种能在数轴上画出无理数对应点的方法.
(1)图2中A、B两点表示的数分别为 ﹣ , ;
(2)请你参考以上方法:
①把图3中5×1的长方形进行剪裁,并拼成一个大正方形,在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a= .(注:小正方形边长都是1,拼接不重叠也无空隙)
②在①的基础上,参考图2的画法,在数轴上用M表示数a,图中标出必要线段长.
解:(1)由题意,OA=OB=,
∴A点表示﹣,B点表示.
故答案为:﹣,.
(2)图形如图所示:大正方形的边长a==,
故答案为:.
(3)如图,点M即为所求.
中小学教育资源及组卷应用平台
一.选择题(共8小题)
1.如图,在△ABC中,∠C=90°,AB+BC=8,AC=4,则△ABC的面积为( )
A.6 B.7.5 C.10 D.12
2.已知直角三角形的斜边长为15,一直角边长为12,则另一条直角边长为( )
A. B.3 C.27 D.9
3.三个正方形的面积如图所示,则S的值为( )
A.3 B.12 C.9 D.4
4.若直角三角形的两条边长分别为a、b,且满足a=3,b=4,则该直角三角形的第三边的长为( )
A.5 B. C.5或 D.不确定
5.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
6.如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点A,B,C均在网格的格点上,则△ABC的三条边中边长是无理数的有( )
A.0条 B.1条 C.2条 D.3条
7.如图所示,数轴上点A、B分别对应1、2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴正半轴于点M,则点M所对应的数为( )
A. B. C. D.
8.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是( )
A.148 B.100 C.196 D.144
二.填空题(共4小题)
9.如图,以直角三角形的三边为边,分别向直角三角形外部作等边三角形,三个等边三角形的面积分别为S1,S2,S3.则它们满足的数量关系为 .
10.Rt△ABC中,∠B=90°,D为BC上的一点,若DC=DA=5,△ACD的面积为10,则BD的长为 .
11.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影部分是一个小正方形EFGH,这样就组成一个“赵爽弦图”.若AB=10,AE=8,则正方形EFGH的面积为 .
12.如图,三个直角三角形(Ⅰ,Ⅱ,Ⅲ)拼成一个直角梯形(两底分别为a、b,高为a+b),利用这个图形,小明验证了勾股定理.请你填写计算过程中留下的空格:
S梯形= (a+b),即S梯形=( )①
S梯形=Ⅰ+Ⅱ+Ⅲ(罗马数字表示相应图形的面积)
= + + ,即S梯形=( )②
由①、②,得a2+b2=c2.
三.解答题(共4小题)
13.如图,在Rt△ABC中,∠ACB=90°,AB=26,AC=24,点D为△ABC外一点,连接BD,CD,测得CD=8,BD=6,求四边形ABDC的面积.
14.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
15.如图,每个小正方形的边长都为1,点A,B,C,D都在格点上.
(1)求四边形ABCD的周长;
(2)判断∠ABC是不是直角?并说明理由.
16.如图,把两个边长为1的小正方形沿着对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形,由此得到了一种能在数轴上画出无理数对应点的方法.
(1)图2中A、B两点表示的数分别为 , ;
(2)请你参考以上方法:
①把图3中5×1的长方形进行剪裁,并拼成一个大正方形,在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a= .(注:小正方形边长都是1,拼接不重叠也无空隙)
②在①的基础上,参考图2的画法,在数轴上用M表示数a,图中标出必要线段长.
2.7探索勾股定理 同步练习
参考答案与试题解析
一.选择题(共8小题)
1.如图,在△ABC中,∠C=90°,AB+BC=8,AC=4,则△ABC的面积为( )
A.6 B.7.5 C.10 D.12
解:设BC=x,
∵AB+BC=8,
∴AB=8﹣x,
在Rt△ABC中,∠C=90°,
∴AB2=BC2+AC2,
∴x2+42=(8﹣x)2,
∴x=3,
∴BC=3,
∴S===6,
即△ABC的面积为6,
故选:A.
2.已知直角三角形的斜边长为15,一直角边长为12,则另一条直角边长为( )
A. B.3 C.27 D.9
解:∵直角三角形的斜边长为15,一直角边长为12,
∴另一条直角边长=,
故选:D.
3.三个正方形的面积如图所示,则S的值为( )
A.3 B.12 C.9 D.4
解:如图,
由题意可得:AB=4,AC=5,
∵AC2=AB2+BC2,
∴BC2=25﹣16=9,
∴S=9,
故选:C.
4.若直角三角形的两条边长分别为a、b,且满足a=3,b=4,则该直角三角形的第三边的长为( )
A.5 B. C.5或 D.不确定
解:①当a,b为两直角边时,根据勾股定理,
第三边长为:==5,
且3+4>5,
②当b为斜边长时,根据勾股定理,
第三边长为:=,
且3+>4,
∴该直角三角形的第三边的长为5或,
故选:C.
5.勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )
A. B. C. D.
解:A、∵ab+c2+ab=(a+b)(a+b),
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
B、∵4×ab+c2=(a+b)2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
C、∵4×ab+(b﹣a)2=c2,
∴整理得:a2+b2=c2,即能证明勾股定理,故本选项不符合题意;
D、根据图形不能证明勾股定理,故本选项符合题意;
故选:D.
6.如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点A,B,C均在网格的格点上,则△ABC的三条边中边长是无理数的有( )
A.0条 B.1条 C.2条 D.3条
解:由勾股定理得:AB=,是无理数;
BC=,是无理数;
AC=,是有理数.
∴△ABC的三条边中边长是无理数的有2条,
故选:C.
7.如图所示,数轴上点A、B分别对应1、2,过点B作PQ⊥AB,以点B为圆心,AB长为半径画弧,交PQ于点C,以原点O为圆心,OC长为半径画弧,交数轴正半轴于点M,则点M所对应的数为( )
A. B. C. D.
解:∵OA=1,OB=2,
∴AB=1,
由作图可知:OB=2,BC=AB=1,∠OBC=90°,
∴OM=OC=,
∴点M所对应的数为,
故选:B.
8.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图所示的“数学风车”,则这个风车的外围周长是( )
A.148 B.100 C.196 D.144
解:设将CA延长到点D,连接BD,
根据题意,得CD=12×2=24,BC=7,
∵∠BCD=90°,
∴BC2+CD2=BD2,即72+242=BD2,
∴BD=25,
∴AD+BD=12+25=37,
∴这个风车的外围周长是37×4=148.
故选:A.
二.填空题(共4小题)
9.如图,以直角三角形的三边为边,分别向直角三角形外部作等边三角形,三个等边三角形的面积分别为S1,S2,S3.则它们满足的数量关系为 S1+S2=S3 .
解:设AC=a,BC=b,AB=c,
∵△ABC是直角三角形,
∴a2+b2=c2,
∴a2+b2=c2,
又∵S1=×sin60°a a=a2,S2=b2,S3=c2,
∴S1+S2=S3,
故答案是:S1+S2=S3.
10.Rt△ABC中,∠B=90°,D为BC上的一点,若DC=DA=5,△ACD的面积为10,则BD的长为 3 .
解:设BD=x,
在Rt△ABD中,由勾股定理得:AB==,
∵△ACD的面积为10,
∴×DC×AB=10,即×5×=10,
解得:x1=3,x2=﹣3(舍去),
∴BD的长为3,
故答案为:3.
11.如图,四个全等的直角三角形围成一个大正方形ABCD,中间阴影部分是一个小正方形EFGH,这样就组成一个“赵爽弦图”.若AB=10,AE=8,则正方形EFGH的面积为 4 .
解:直角三角形直角边的较短边为=6,
正方形EFGH的面积=10×10﹣8×6÷2×4=100﹣96=4.
故答案为:4.
12.如图,三个直角三角形(Ⅰ,Ⅱ,Ⅲ)拼成一个直角梯形(两底分别为a、b,高为a+b),利用这个图形,小明验证了勾股定理.请你填写计算过程中留下的空格:
S梯形= (a+b),即S梯形=( a2+2ab+b2 )①
S梯形=Ⅰ+Ⅱ+Ⅲ(罗马数字表示相应图形的面积)
= ab + c2 + ab ,即S梯形=( 2ab+c2 )②
由①、②,得a2+b2=c2.
解:因为,
又因为S梯形=Ⅰ+Ⅱ+Ⅲ=ab+c2+ab=,
所以=,
得c2=a2+b2.
故答案为:a2+2ab+b2,ab,c2,ab,2ab+c2.
三.解答题(共4小题)
13.如图,在Rt△ABC中,∠ACB=90°,AB=26,AC=24,点D为△ABC外一点,连接BD,CD,测得CD=8,BD=6,求四边形ABDC的面积.
解:在Rt△ABC中,∠ACB=90°,
由勾股定理得:BC=,
∵CD=8,BD=6,
∴CD2+BD2=82+62=100,
AC2=100,
∴CD2+BD2=AC2,
∴∠D=90°,
∴S四边形ABDC=S△ABC+S△BCD
=
=
=144.
14.已知:如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
解:(1)在Rt△ABC中,由勾股定理得:BC===4(cm);
(2)由题意得:BP=tcm,分两种情况:
①当∠APB=90°时,如图1所示:
点P与点C重合,
∴BP=BC=4cm,
∴t=4;
综上所述,当△ABP为直角三角形时,t的值为4s或s.
15.如图,每个小正方形的边长都为1,点A,B,C,D都在格点上.
(1)求四边形ABCD的周长;
(2)判断∠ABC是不是直角?并说明理由.
解:(1)由勾股定理可得:AB=,BC=,
CD=,AD=,
∴四边形ABCD的周长=2,
(2)∠ABC是直角,理由如下:
连接AC,由勾股定理可得:AC=,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
∴∠ABC是直角.
26.如图,把两个边长为1的小正方形沿着对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形,由此得到了一种能在数轴上画出无理数对应点的方法.
(1)图2中A、B两点表示的数分别为 ﹣ , ;
(2)请你参考以上方法:
①把图3中5×1的长方形进行剪裁,并拼成一个大正方形,在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长a= .(注:小正方形边长都是1,拼接不重叠也无空隙)
②在①的基础上,参考图2的画法,在数轴上用M表示数a,图中标出必要线段长.
解:(1)由题意,OA=OB=,
∴A点表示﹣,B点表示.
故答案为:﹣,.
(2)图形如图所示:大正方形的边长a==,
故答案为:.
(3)如图,点M即为所求.
中小学教育资源及组卷应用平台
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
