3.3 方差和标准差 课件(共22张PPT)
文档属性
| 名称 | 3.3 方差和标准差 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-10 15:45:03 | ||
图片预览







文档简介
(共22张PPT)
浙教版八下数学
第三章 数据分析初步
3.3 方差和标准差
皮埃尔
徳
顾拜旦:
现代奥林匹克之父
第28届夏季奥林匹克运动会:2004年8月13日~29日在希腊首都雅典举行
雅典奥运会男子步枪三姿决赛,美国选手埃蒙斯在前9枪的发挥中十分稳定,也比对手足足高出了3环,
最后一枪成功将子弹送到了隔壁家伙的靶子上,居然还是一个惊人的10.6环,把近在咫尺的金牌拱手让给了中国老将贾占波。
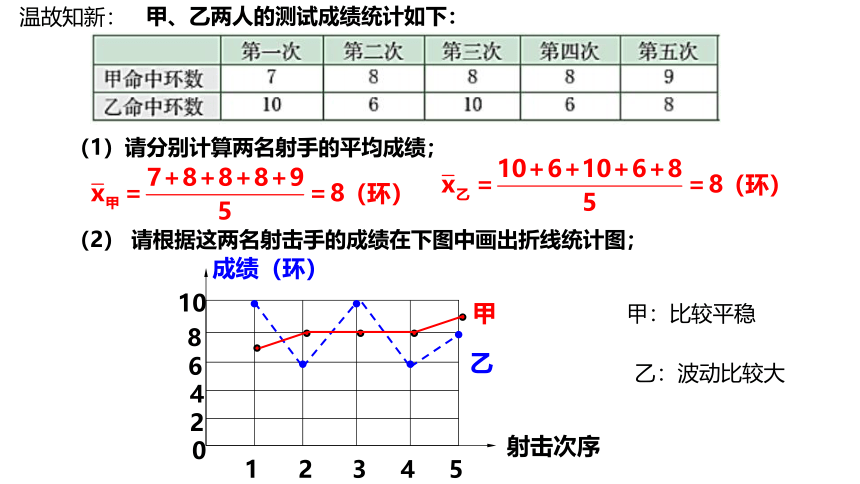
甲、乙两人的测试成绩统计如下:
(1)请分别计算两名射手的平均成绩;
(2) 请根据这两名射击手的成绩在下图中画出折线统计图;
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
乙
甲
甲:比较平稳
乙:波动比较大
温故知新:
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
乙
甲
甲:比较平稳
乙:波动比较大
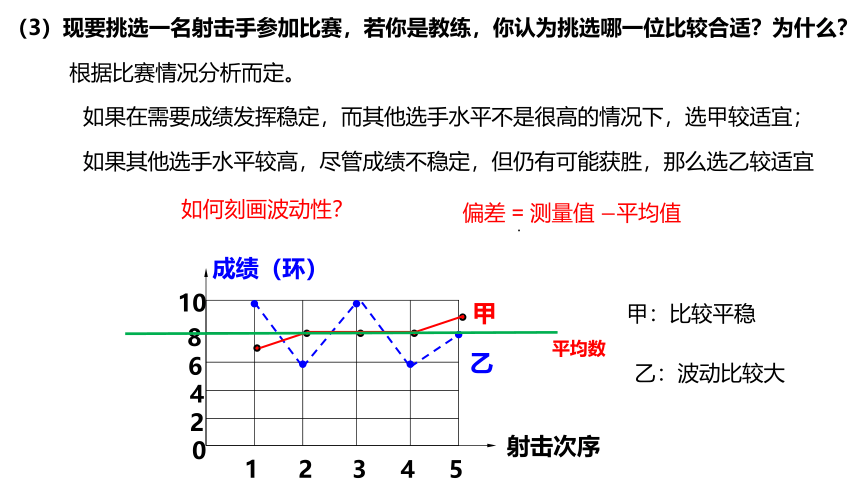
(3)现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较合适?为什么?
根据比赛情况分析而定。
如果在需要成绩发挥稳定,而其他选手水平不是很高的情况下,选甲较适宜;
如果其他选手水平较高,尽管成绩不稳定,但仍有可能获胜,那么选乙较适宜
偏差 = 测量值 平均值
.
平均数
如何刻画波动性?
甲射击成绩与平均成绩的偏差的和:
(7-8)+(8-8)+(8-8)+(8-8)+(9-8)=0
乙射击成绩与平均成绩的偏差的和:
(10-8)+(6-8)+(10-8)+(6-8)+(8-8)=0
②计算甲、乙两人每次射击成绩与平均成绩的偏差的平方和
①甲、乙两名射击手他们每次射击成绩与他们的平均成绩的偏差的和:
甲射击成绩与平均成绩的偏差的平方和:
(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2=2;
乙射击成绩与平均成绩的偏差的平方和:
(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=16
各偏差的平方和的大小还与射击的次数有关,
用各偏差平方的平均数来衡量数据的稳定性。
一般地,各数据与它们的平均数的差的平方的平均数
叫做这组数据的方差.
方差越小,这组数据的离散程度越小,数据就越集中,越稳定,
方差越大,说明数据的波动越大,越不稳定。
为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问:哪种小麦长得比较整齐
因为S2甲甲的方差:S2甲=
【(13-12)2+(13-13)2+(14-13)2++(11-13)2】=3.6
乙的方差:S2乙=
【(11-13)2+(16-13)2+(17-13)2++(16-13)2】=15.8
(12+13+14+15+10+16+13+11+15+11)=13(cm);
.
(11+16+17+14+13+19+6+8+10+16)=13(cm);
.
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
各数据与它们的平均数的差的平方的平均数.
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
方差用来衡量一批数据的波动大小.(即这批数
据偏离平均数的大小)
n表示样本容量; x表示样本平均数
方差:
归纳小结:
数据的单位与方差的单位不一致
方差的单位是数据单位的平方.
为了使单位一致,可用方差的算术平方根来表示,并把它叫做标准差.
(1)计算:数据1、2、3、4、5的方差。
x
.
=3
S2 =
.
S2 = 2
.
夯实基础,稳扎稳打
S2 =
.
D
A
(4)计算:数据4、4、4、4、4的方差、标准差。
x
.
=4
S2 =
.
S2 = 0
.
S=0
S2 =
.
每个数都一样,说明数据没有偏差,方差与标准差都为0.
(5)计算:数据-1、-2、3、0、5 的方差、标准差。
x
.
=1
S2 =
.
S2 = 6.8
.
.
.
S2 =
.
D
结论:新数据的平均数比原数据的平均数小97,
新数据和原数据的波动情况完全相同,
即新数据和原数据的方差相同
连续递推,豁然开朗
(7)
30
2
x上
.
=20
S上2 =
=2.5
x下
.
=20
=
S下2 =
=2.375
S上2
>S下2
下午气温更稳定
(9)
浙教版八下数学
第三章 数据分析初步
3.3 方差和标准差
皮埃尔
徳
顾拜旦:
现代奥林匹克之父
第28届夏季奥林匹克运动会:2004年8月13日~29日在希腊首都雅典举行
雅典奥运会男子步枪三姿决赛,美国选手埃蒙斯在前9枪的发挥中十分稳定,也比对手足足高出了3环,
最后一枪成功将子弹送到了隔壁家伙的靶子上,居然还是一个惊人的10.6环,把近在咫尺的金牌拱手让给了中国老将贾占波。
甲、乙两人的测试成绩统计如下:
(1)请分别计算两名射手的平均成绩;
(2) 请根据这两名射击手的成绩在下图中画出折线统计图;
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
乙
甲
甲:比较平稳
乙:波动比较大
温故知新:
0
1
2
2
3
4
5
4
6
8
10
射击次序
成绩(环)
乙
甲
甲:比较平稳
乙:波动比较大
(3)现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较合适?为什么?
根据比赛情况分析而定。
如果在需要成绩发挥稳定,而其他选手水平不是很高的情况下,选甲较适宜;
如果其他选手水平较高,尽管成绩不稳定,但仍有可能获胜,那么选乙较适宜
偏差 = 测量值 平均值
.
平均数
如何刻画波动性?
甲射击成绩与平均成绩的偏差的和:
(7-8)+(8-8)+(8-8)+(8-8)+(9-8)=0
乙射击成绩与平均成绩的偏差的和:
(10-8)+(6-8)+(10-8)+(6-8)+(8-8)=0
②计算甲、乙两人每次射击成绩与平均成绩的偏差的平方和
①甲、乙两名射击手他们每次射击成绩与他们的平均成绩的偏差的和:
甲射击成绩与平均成绩的偏差的平方和:
(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2=2;
乙射击成绩与平均成绩的偏差的平方和:
(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=16
各偏差的平方和的大小还与射击的次数有关,
用各偏差平方的平均数来衡量数据的稳定性。
一般地,各数据与它们的平均数的差的平方的平均数
叫做这组数据的方差.
方差越小,这组数据的离散程度越小,数据就越集中,越稳定,
方差越大,说明数据的波动越大,越不稳定。
为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):
甲: 12 13 14 15 10 16 13 11 15 11
乙: 11 16 17 14 13 19 6 8 10 16
问:哪种小麦长得比较整齐
因为S2甲
【(13-12)2+(13-13)2+(14-13)2++(11-13)2】=3.6
乙的方差:S2乙=
【(11-13)2+(16-13)2+(17-13)2++(16-13)2】=15.8
(12+13+14+15+10+16+13+11+15+11)=13(cm);
.
(11+16+17+14+13+19+6+8+10+16)=13(cm);
.
S2= [(x1-x)2+ (x2-x)2 +…+ (xn-x)2 ]
1
n
各数据与它们的平均数的差的平方的平均数.
计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.
方差用来衡量一批数据的波动大小.(即这批数
据偏离平均数的大小)
n表示样本容量; x表示样本平均数
方差:
归纳小结:
数据的单位与方差的单位不一致
方差的单位是数据单位的平方.
为了使单位一致,可用方差的算术平方根来表示,并把它叫做标准差.
(1)计算:数据1、2、3、4、5的方差。
x
.
=3
S2 =
.
S2 = 2
.
夯实基础,稳扎稳打
S2 =
.
D
A
(4)计算:数据4、4、4、4、4的方差、标准差。
x
.
=4
S2 =
.
S2 = 0
.
S=0
S2 =
.
每个数都一样,说明数据没有偏差,方差与标准差都为0.
(5)计算:数据-1、-2、3、0、5 的方差、标准差。
x
.
=1
S2 =
.
S2 = 6.8
.
.
.
S2 =
.
D
结论:新数据的平均数比原数据的平均数小97,
新数据和原数据的波动情况完全相同,
即新数据和原数据的方差相同
连续递推,豁然开朗
(7)
30
2
x上
.
=20
S上2 =
=2.5
x下
.
=20
=
S下2 =
=2.375
S上2
>S下2
下午气温更稳定
(9)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
