6.1切线[下学期]
图片预览




文档简介
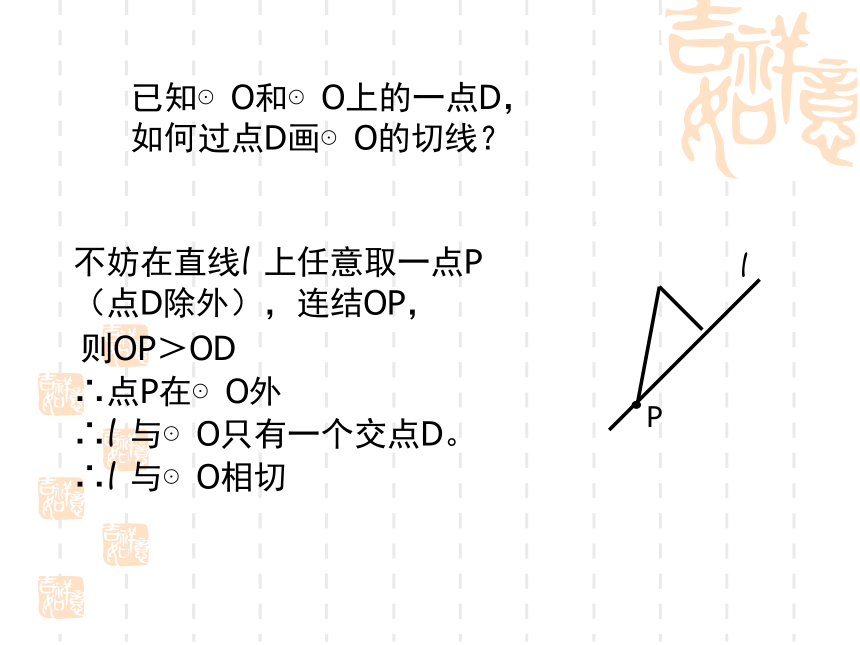
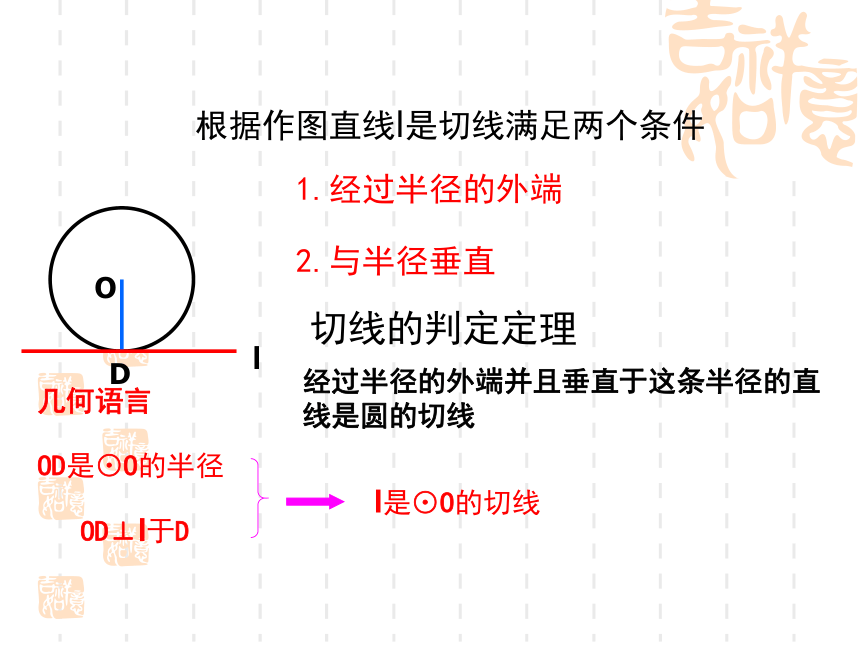
课件17张PPT。6.1 圆的切线当直线与圆有唯一公共点时,叫做直线和圆相切。其中的直线叫做圆的切线。唯一的公共点叫做切点。已知⊙O和⊙O上的一点D,如何过点D画⊙O的切线?不妨在直线l 上任意取一点P(点D除外),连结OP,则OP>OD∴点P在⊙O外∴l 与⊙O只有一个交点D。∴l 与⊙O相切1.经过半径的外端2.与半径垂直切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线几何语言OD是⊙O的半径OD⊥l于D定理说明:证明:连结OB∵OB=OC,AB=BC,∠C=30°
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∴∠ABO=180°-(∠AOB+∠A)
=180°-(60°+30°)
=90°
∴ AB是⊙O的切线题目中“半径”已有,只需证“垂直”即可得直线与圆相切。证明:连OC、BC,
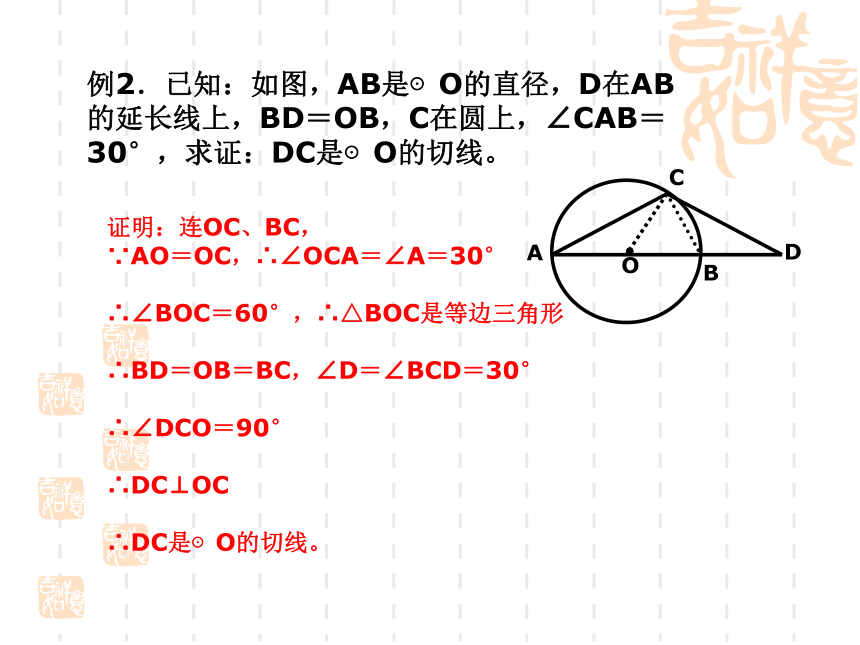
∵AO=OC,∴∠OCA=∠A=30° ∴∠BOC=60°,∴△BOC是等边三角形 ∴BD=OB=BC,∠D=∠BCD=30° ∴∠DCO=90° ∴DC⊥OC ∴DC是⊙O的切线。 例3.已知:如图,⊙O的半径为4cm,OA⊥OB,
OC⊥AB于C,OB=4 cm,OA=2 cm,
求证:AB与⊙O相切。 证明:∵OA⊥OB,OC⊥AB
∴△AOB是直角三角形 又∵OA=2 cm,OB=4 cm
∴AB=10 根据三角形面积公式有:AB·OC=OA·OB ∴OC= 4(cm),OC是⊙O的半径。 直线AB经过半径OC的外端C,并且垂直于
半径OC所 以AB与 ⊙O相切。 题目中“垂直”已有,只需证“距离等于半径”,即可得直线与圆相切。例4:当圆心到直线的距离等于圆的半径时,该直线是这个圆的切线已知:⊙O的圆心O到直线l 的距 离等于⊙O的半径r。求证:直线l 是⊙O的切线证明:过点O作OA⊥l ,A为垂足。∵OA=d=r ∴点A在⊙O上∴OA是⊙O的半径∴ l 是⊙O的切线题目的条件中“垂直”和“距离等于半径”都没有明确显示出来,就必须先作出“垂直”,再证“距离等于半径” 如图,△ABC内接于⊙O,∠B=∠C,小圆与AB相切,求证:AC为小圆的切线。 ????????????????????? 证明:作OE⊥AC于E,OD⊥AB于D
设小圆的半径为r。 ∵∠B=∠C,∴AB=AC,
∴OD=OE 又∵AB与小圆相切,
∴OD=r,∴OE=r 故由切线判定定理知,AC为小圆切线。
练习1 已知点B在⊙O上。根据下列条件,能否判定直线AB和⊙O相切?
(1)OB=7,AO=12,AB=5;
(2) ∠O=68.5°, ∠A=21.5°;
(3)tgA= 返回返回练习3 Rt△ABC内接于⊙O, ∠A=30°。延长斜边AB到D,使BD等于⊙O的半径,求证:DC是⊙O的切线。
课堂练习:1.判断: (1)经过半径的一个端点,并且垂直于这条半径的直线是圆的切线
(2)若一条直线与圆的半径垂直,则这条直线是圆的切线 (3)以直角边为半径的圆一定与另一条直角边相切。 (4)以等腰直角三角形斜边的中点为圆心,直角边的一半为半径的圆,与 两条直角边相切。 小结一 判定一条直线是圆的切线有三种方法1 根据定义直线与圆有唯一的公共点2 根据判定定理3,根据例1圆心到直线的距离等于半径 二 添辅助线的方法连接圆心与交点过圆心作直线的垂线段课后作业:1.如图,已知:在△ABC中,AB=AC,以AB为直径作⊙O交BC于D,DE⊥AC于E, 求证:DE是⊙O的切线。 ?????????????????????? 分析:因为DE经过⊙O上的点D,所以要证明DE为切线,可连结OD, 再证明DE⊥OD。 2.如图(10),已知在△ABC中,AD⊥BC于D,AD= ?BC,E和F分别为AB和 AC的中点,EF与AD交于G,以EF为直径作⊙O,求证:⊙O与BC相切分析:∵PA过⊙O上一点A,要证PA为切线,只要证PA⊥AO,为此,作 半径AO,只要证PA⊥AO即可。 3.如图,△ABC内接于⊙O,P、B、C在一直线上,且PA2=PB·PC, 求证:PA是⊙O的切线。
∴∠OBC=∠C=∠A=30°
∴∠AOB=∠C+∠OBC=60°
∴∠ABO=180°-(∠AOB+∠A)
=180°-(60°+30°)
=90°
∴ AB是⊙O的切线题目中“半径”已有,只需证“垂直”即可得直线与圆相切。证明:连OC、BC,
∵AO=OC,∴∠OCA=∠A=30° ∴∠BOC=60°,∴△BOC是等边三角形 ∴BD=OB=BC,∠D=∠BCD=30° ∴∠DCO=90° ∴DC⊥OC ∴DC是⊙O的切线。 例3.已知:如图,⊙O的半径为4cm,OA⊥OB,
OC⊥AB于C,OB=4 cm,OA=2 cm,
求证:AB与⊙O相切。 证明:∵OA⊥OB,OC⊥AB
∴△AOB是直角三角形 又∵OA=2 cm,OB=4 cm
∴AB=10 根据三角形面积公式有:AB·OC=OA·OB ∴OC= 4(cm),OC是⊙O的半径。 直线AB经过半径OC的外端C,并且垂直于
半径OC所 以AB与 ⊙O相切。 题目中“垂直”已有,只需证“距离等于半径”,即可得直线与圆相切。例4:当圆心到直线的距离等于圆的半径时,该直线是这个圆的切线已知:⊙O的圆心O到直线l 的距 离等于⊙O的半径r。求证:直线l 是⊙O的切线证明:过点O作OA⊥l ,A为垂足。∵OA=d=r ∴点A在⊙O上∴OA是⊙O的半径∴ l 是⊙O的切线题目的条件中“垂直”和“距离等于半径”都没有明确显示出来,就必须先作出“垂直”,再证“距离等于半径” 如图,△ABC内接于⊙O,∠B=∠C,小圆与AB相切,求证:AC为小圆的切线。 ????????????????????? 证明:作OE⊥AC于E,OD⊥AB于D
设小圆的半径为r。 ∵∠B=∠C,∴AB=AC,
∴OD=OE 又∵AB与小圆相切,
∴OD=r,∴OE=r 故由切线判定定理知,AC为小圆切线。
练习1 已知点B在⊙O上。根据下列条件,能否判定直线AB和⊙O相切?
(1)OB=7,AO=12,AB=5;
(2) ∠O=68.5°, ∠A=21.5°;
(3)tgA= 返回返回练习3 Rt△ABC内接于⊙O, ∠A=30°。延长斜边AB到D,使BD等于⊙O的半径,求证:DC是⊙O的切线。
课堂练习:1.判断: (1)经过半径的一个端点,并且垂直于这条半径的直线是圆的切线
(2)若一条直线与圆的半径垂直,则这条直线是圆的切线 (3)以直角边为半径的圆一定与另一条直角边相切。 (4)以等腰直角三角形斜边的中点为圆心,直角边的一半为半径的圆,与 两条直角边相切。 小结一 判定一条直线是圆的切线有三种方法1 根据定义直线与圆有唯一的公共点2 根据判定定理3,根据例1圆心到直线的距离等于半径 二 添辅助线的方法连接圆心与交点过圆心作直线的垂线段课后作业:1.如图,已知:在△ABC中,AB=AC,以AB为直径作⊙O交BC于D,DE⊥AC于E, 求证:DE是⊙O的切线。 ?????????????????????? 分析:因为DE经过⊙O上的点D,所以要证明DE为切线,可连结OD, 再证明DE⊥OD。 2.如图(10),已知在△ABC中,AD⊥BC于D,AD= ?BC,E和F分别为AB和 AC的中点,EF与AD交于G,以EF为直径作⊙O,求证:⊙O与BC相切分析:∵PA过⊙O上一点A,要证PA为切线,只要证PA⊥AO,为此,作 半径AO,只要证PA⊥AO即可。 3.如图,△ABC内接于⊙O,P、B、C在一直线上,且PA2=PB·PC, 求证:PA是⊙O的切线。
