第三章 数据分析初步 章末复习------三个数、三个差 课件(共13张PPT)
文档属性
| 名称 | 第三章 数据分析初步 章末复习------三个数、三个差 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 621.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:36:34 | ||
图片预览





文档简介
(共13张PPT)
浙教版八下数学
第三章 数据分析初步 章末复习
-------三个数+三个差
三个数:平均数、众数、中位数-------刻画数据集中趋势
2. 众数:一组数据中出现次数最多的数据
3. 中位数:将一组数据按照由小到大(或由大到小)的顺序排列,
如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;
如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
1.平均数:
算术平均数:
x
.
加权平均数:
x
.
三个差:方差、标准差、极差-------刻画数据离散程度
1
1
2
3
4
2
3
4
5
5
6
6
7
7
8
8
9
9
10
10
射击次序
成绩(环)
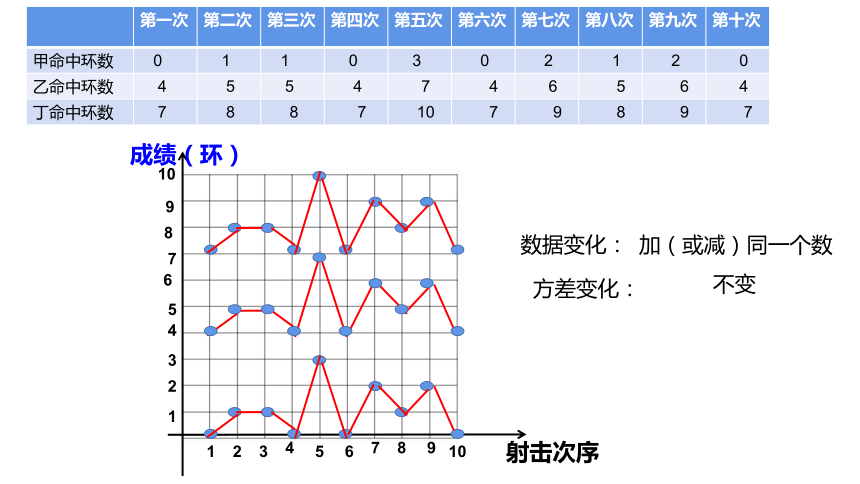
第一次 第二次 第三次 第四次 第五次 第六次 第七次 第八次 第九次 第十次
甲命中环数 0 1 1 0 3 0 2 1 2 0
乙命中环数 4 5 5 4 7 4 6 5 6 4
丁命中环数 7 8 8 7 10 7 9 8 9 7
加(或减)同一个数
不变
数据变化:
方差变化:
2.证明:如果数据x1,x2,…,xn的平均数是x,方差是S2,
那么一组新数据x1+a,x2+a,…,xn+a的平均数是x+a,方差仍是S2
证明:
x
.
+
x
S2=
+
】
x新
.
.
=
x +a
整体替换
S新2=
整体替换
+
x
=
+
]
=S2
3.如果数据x1,x2,…,xn的方差是3,求另一组数据2x1,2x2,…,2xn的方差
解:
x新
.
.
x
.
.
+
x
S原2=
+
】
+
x
+
】=3
=2
x
S新2=
+
x
=
+
】
=12
整体替换
整体替换
4.证明:如果一组数据x1、x2、…、xn的方差是s2,
那么数据kx1、kx2、…、kxn的方差是k2s2(k≠0),
证明:
x
.
+
x
S2 =
+
】
x新
.
.
=k
x
S新2=
+
x
=
+
】
=k2s2
整体替换
5.证明:如果一组数据x1、x2、…、xn的方差是s2,
那么数据kx1+b、kx2+b、…、kxn+b的方差是k2s2(k≠0),
证明:
x
.
+
x
S2 =
+
】
x新
.
.
=k
x +b
+
x
=
+
】
=k2s2
整体替换
S新2=
x
.
.
x新
.
.
=6-2=4
S新2=
+
=
+
】
=27
+
+
】=3
整体替换
整体替换
6.已知一组数据:x1,x2,x3,,xn的平均数是2,方差是3,求
另一组数据:3x1﹣2,3x2﹣2,3x3﹣2,,3xn﹣2的平均数和方差。
.
9=
41=
如果一组数据x1、x2、…、xn的方差是s2,
那么数据kx1+b、kx2+b、…、kxn+b的方差是k2s2(k≠0),
分析:
退一步海阔天空:
S2 =
=
S2 =
=
停一刻,静观其变
= 4
进一步,胜利在望
4a
7.数据1、2、3、4、5
求数据3、5、7、9、
.
3=
.
5=
.
7=
.
数据1、2、3、4、5
数据3、5、7、9、22a=4a
.
数据1、2、3
.
数据3、5、7
.
1
1
2
3
4
2
3
4
5
5
6
6
7
7
8
8
9
9
10
10
射击次序
成绩(环)
第一次 第二次 第三次 第四次 第五次 第六次 第七次 第八次 第九次 第十次
甲命中环数 2 1 1 2 3 2 2 1 2 1
乙命中环数 4 2 2 4 6 4 4 2 4 2
丁命中环数 6 3 3 6 9 6 6 3 6 3
数据变化:k倍
方差变化:k2倍
基准:2022
新数据:
-2、-1、0、1、2
x
.
=0
S2 =
S2 = 2
.
基准:2019
新数据1、2、3、4、5
x
.
=3
S2 =
.
S2 = 2
8.求数据2020、2021、2022、2023、2024
.
S2 =
.
浙教版八下数学
第三章 数据分析初步 章末复习
-------三个数+三个差
三个数:平均数、众数、中位数-------刻画数据集中趋势
2. 众数:一组数据中出现次数最多的数据
3. 中位数:将一组数据按照由小到大(或由大到小)的顺序排列,
如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;
如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
1.平均数:
算术平均数:
x
.
加权平均数:
x
.
三个差:方差、标准差、极差-------刻画数据离散程度
1
1
2
3
4
2
3
4
5
5
6
6
7
7
8
8
9
9
10
10
射击次序
成绩(环)
第一次 第二次 第三次 第四次 第五次 第六次 第七次 第八次 第九次 第十次
甲命中环数 0 1 1 0 3 0 2 1 2 0
乙命中环数 4 5 5 4 7 4 6 5 6 4
丁命中环数 7 8 8 7 10 7 9 8 9 7
加(或减)同一个数
不变
数据变化:
方差变化:
2.证明:如果数据x1,x2,…,xn的平均数是x,方差是S2,
那么一组新数据x1+a,x2+a,…,xn+a的平均数是x+a,方差仍是S2
证明:
x
.
+
x
S2=
+
】
x新
.
.
=
x +a
整体替换
S新2=
整体替换
+
x
=
+
]
=S2
3.如果数据x1,x2,…,xn的方差是3,求另一组数据2x1,2x2,…,2xn的方差
解:
x新
.
.
x
.
.
+
x
S原2=
+
】
+
x
+
】=3
=2
x
S新2=
+
x
=
+
】
=12
整体替换
整体替换
4.证明:如果一组数据x1、x2、…、xn的方差是s2,
那么数据kx1、kx2、…、kxn的方差是k2s2(k≠0),
证明:
x
.
+
x
S2 =
+
】
x新
.
.
=k
x
S新2=
+
x
=
+
】
=k2s2
整体替换
5.证明:如果一组数据x1、x2、…、xn的方差是s2,
那么数据kx1+b、kx2+b、…、kxn+b的方差是k2s2(k≠0),
证明:
x
.
+
x
S2 =
+
】
x新
.
.
=k
x +b
+
x
=
+
】
=k2s2
整体替换
S新2=
x
.
.
x新
.
.
=6-2=4
S新2=
+
=
+
】
=27
+
+
】=3
整体替换
整体替换
6.已知一组数据:x1,x2,x3,,xn的平均数是2,方差是3,求
另一组数据:3x1﹣2,3x2﹣2,3x3﹣2,,3xn﹣2的平均数和方差。
.
9=
41=
如果一组数据x1、x2、…、xn的方差是s2,
那么数据kx1+b、kx2+b、…、kxn+b的方差是k2s2(k≠0),
分析:
退一步海阔天空:
S2 =
=
S2 =
=
停一刻,静观其变
= 4
进一步,胜利在望
4a
7.数据1、2、3、4、5
求数据3、5、7、9、
.
3=
.
5=
.
7=
.
数据1、2、3、4、5
数据3、5、7、9、22a=4a
.
数据1、2、3
.
数据3、5、7
.
1
1
2
3
4
2
3
4
5
5
6
6
7
7
8
8
9
9
10
10
射击次序
成绩(环)
第一次 第二次 第三次 第四次 第五次 第六次 第七次 第八次 第九次 第十次
甲命中环数 2 1 1 2 3 2 2 1 2 1
乙命中环数 4 2 2 4 6 4 4 2 4 2
丁命中环数 6 3 3 6 9 6 6 3 6 3
数据变化:k倍
方差变化:k2倍
基准:2022
新数据:
-2、-1、0、1、2
x
.
=0
S2 =
S2 = 2
.
基准:2019
新数据1、2、3、4、5
x
.
=3
S2 =
.
S2 = 2
8.求数据2020、2021、2022、2023、2024
.
S2 =
.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
