7.4 一次函数的图象(1) [上学期]
文档属性
| 名称 | 7.4 一次函数的图象(1) [上学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 271.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-07 00:00:00 | ||
图片预览



文档简介
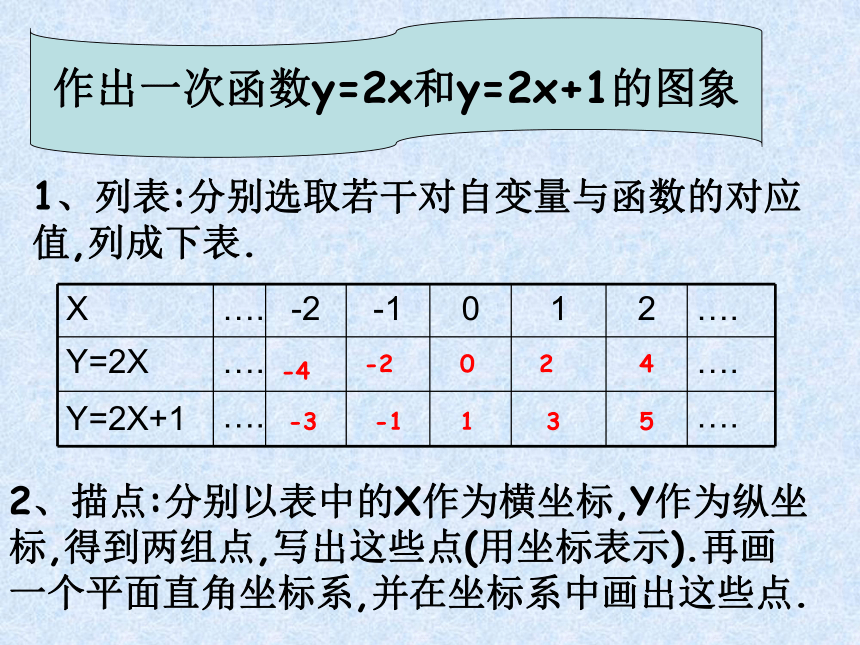
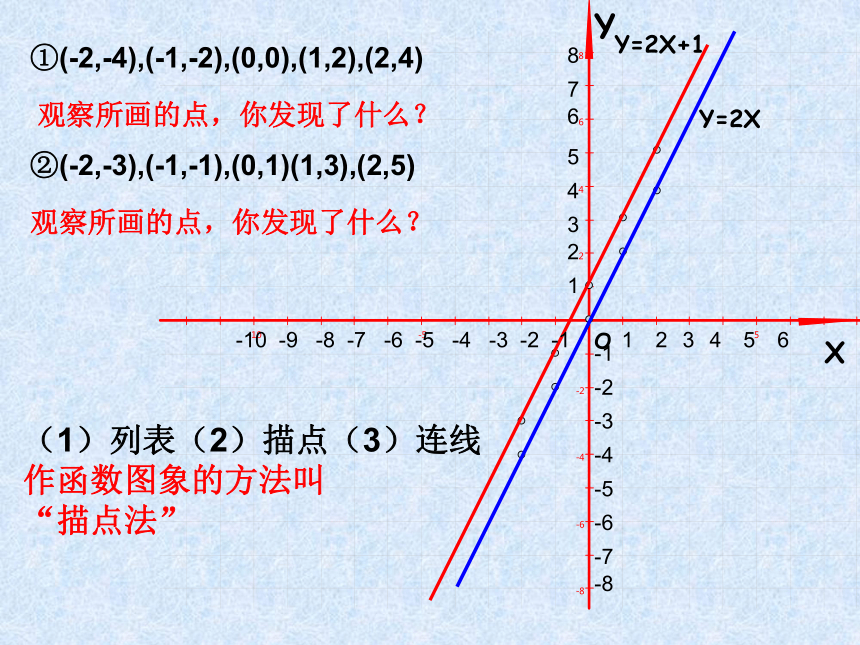
课件15张PPT。右边的图象表示的是甲、乙两人在一次赛跑中路程s与时间t的函数图象。根据图象回答下列问题:(1)这是一次几百米的赛跑?(2)甲、乙两人中谁先到达终点?(3)乙在这次赛跑中的速度是多少?我们来赛跑在直角坐标系内描出它的对应点,所有这些点组成的图形叫做函数的图象。 函 数的 图 象 当t=3时,s=25,得到点(3,25)。像这样,把一个函数的自变量t与对应的函数s的值分别作为点的横坐标和纵坐标。7.4一次函数的图象作出一次函数y=2x和y=2x+1的图象1、列表:分别选取若干对自变量与函数的对应值,列成下表.2、描点:分别以表中的X作为横坐标,Y作为纵坐标,得到两组点,写出这些点(用坐标表示).再画一个平面直角坐标系,并在坐标系中画出这些点.-4-3-2-1012345Y=2X+1YXOY=2XY=2X+1 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1-2-3-4-5-612345612345678-7-8①(-2,-4),(-1,-2),(0,0),(1,2),(2,4)②(-2,-3),(-1,-1),(0,1)(1,3),(2,5)观察所画的点,你发现了什么?观察所画的点,你发现了什么?(1)列表(2)描点(3)连线作函数图象的方法叫
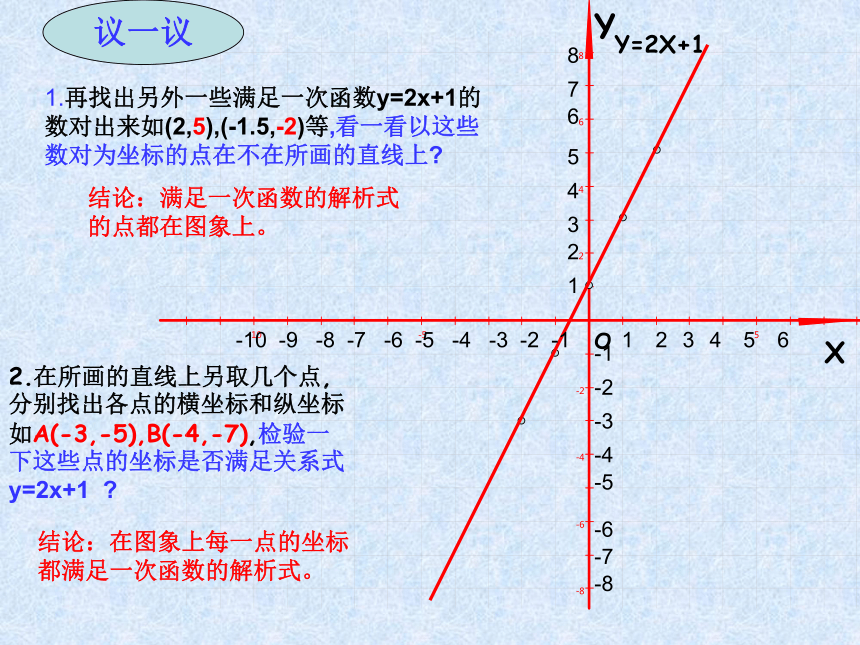
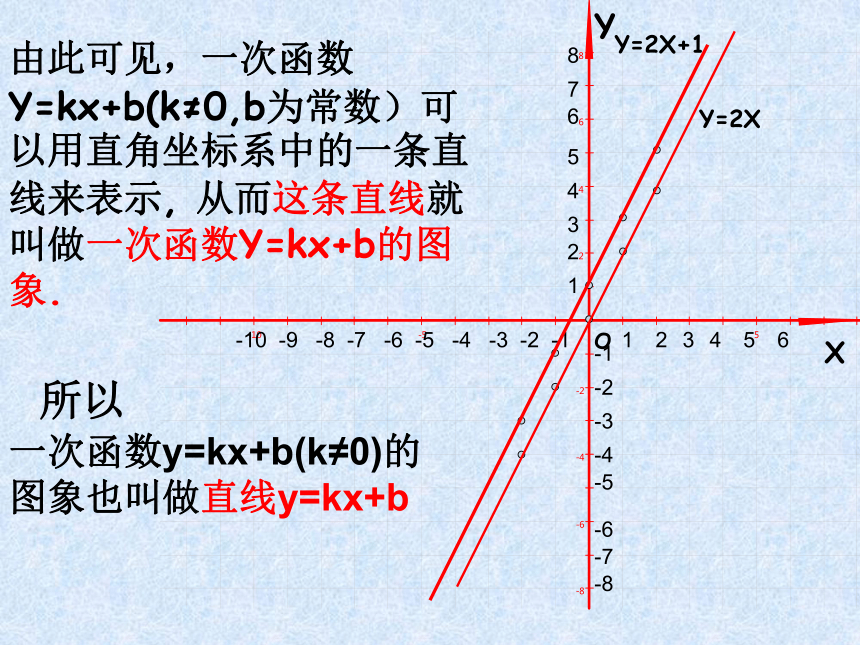
“描点法”Y2.在所画的直线上另取几个点,分别找出各点的横坐标和纵坐标如A(-3,-5),B(-4,-7),检验一下这些点的坐标是否满足关系式y=2x+1 ?1.再找出另外一些满足一次函数y=2x+1的数对出来如(2,5),(-1.5,-2)等,看一看以这些数对为坐标的点在不在所画的直线上?议一议结论:满足一次函数的解析式的点都在图象上。结论:在图象上每一点的坐标都满足一次函数的解析式。Y由此可见,一次函数Y=kx+b(k≠0,b为常数)可以用直角坐标系中的一条直线来表示, 从而这条直线就叫做一次函数Y=kx+b的图象. -10 -9 -8 -7 -6 -5 -4 -3 -2 -1一次函数y=kx+b(k≠0)的图象也叫做直线y=kx+b所以例1:在同一坐标系作出下列函数的图象,并求它们
与坐标轴的交点坐标.Y=3x, y=-3x+2过点(0,0)与点(1,3)画直线Y=3X。YXO123123-1-1-2Y=3XY=-3X+2问题:你会找哪些点?和你的同桌讨论,取哪些点画图时比较方便?你能直接利用函数解析式求函数图象与坐标轴交点的坐标吗?想一想过点(0,2)与点(1,-1)画直线Y=-3X+2。由图象看出它与坐标轴的交点是什么?由图象看出它与坐标轴的交点为原点(0,0)。比一比,看谁画得快!想一想,说一说 1.下列各点中,哪些点在函数y=4x+1的图象上?哪些不在函数的图象上?
A(2, 9)。B(5, 1)。C(-1, -3)。D(-0.5, -1)。2.若函数y=2x-3 的图象经过点(1,a) ,(b, 2)两点, 则a= b=-1 在不在 在 在2.5练 一 练(1≤x≤4)这节课你学到了什么?1、知识方面你学到了哪些?2、你还有什么感受?梳理一下吧! 2、函数图象的概念包含两个方面的内容:
(1)满足函数解析式的任意一对x、y的值描出的点一定
在这个函数的图象上。
(2)在函数图象上的点A(x,y)中的x、y一定满足函
数的解析式。 1、函数图象的概念:
把一个函数的自变量x与对应的函数y的值分别作
为点的横坐标和纵坐标 , 在直角坐标系内描出它的对 应点 , 所有这些点组成的图形叫做该函数的图象. 3、“描点法”作函数图象的一般步骤:
(1)列表; (2)描点;(3)连线
6、函数的代数表达式与函数图象是紧密联系着的,“数”用“形”表示,由“形”想到“数”,这是我们数学学习中一个很重要的思想方法——数形结合。5、画函数图象时还应特别注意:需考虑自变量的取值范围。作业
1.必做题:作业本(2)及课本作业题A组。
2.选做题:课本作业题B、C组。考考你
已知直线y= -2x+4,它与x轴的交点为A,与y轴的交点为B.
(1).求A, B两点的坐标.
(2).求?AOB的面积. (O为坐标原点)
“描点法”Y2.在所画的直线上另取几个点,分别找出各点的横坐标和纵坐标如A(-3,-5),B(-4,-7),检验一下这些点的坐标是否满足关系式y=2x+1 ?1.再找出另外一些满足一次函数y=2x+1的数对出来如(2,5),(-1.5,-2)等,看一看以这些数对为坐标的点在不在所画的直线上?议一议结论:满足一次函数的解析式的点都在图象上。结论:在图象上每一点的坐标都满足一次函数的解析式。Y由此可见,一次函数Y=kx+b(k≠0,b为常数)可以用直角坐标系中的一条直线来表示, 从而这条直线就叫做一次函数Y=kx+b的图象. -10 -9 -8 -7 -6 -5 -4 -3 -2 -1一次函数y=kx+b(k≠0)的图象也叫做直线y=kx+b所以例1:在同一坐标系作出下列函数的图象,并求它们
与坐标轴的交点坐标.Y=3x, y=-3x+2过点(0,0)与点(1,3)画直线Y=3X。YXO123123-1-1-2Y=3XY=-3X+2问题:你会找哪些点?和你的同桌讨论,取哪些点画图时比较方便?你能直接利用函数解析式求函数图象与坐标轴交点的坐标吗?想一想过点(0,2)与点(1,-1)画直线Y=-3X+2。由图象看出它与坐标轴的交点是什么?由图象看出它与坐标轴的交点为原点(0,0)。比一比,看谁画得快!想一想,说一说 1.下列各点中,哪些点在函数y=4x+1的图象上?哪些不在函数的图象上?
A(2, 9)。B(5, 1)。C(-1, -3)。D(-0.5, -1)。2.若函数y=2x-3 的图象经过点(1,a) ,(b, 2)两点, 则a= b=-1 在不在 在 在2.5练 一 练(1≤x≤4)这节课你学到了什么?1、知识方面你学到了哪些?2、你还有什么感受?梳理一下吧! 2、函数图象的概念包含两个方面的内容:
(1)满足函数解析式的任意一对x、y的值描出的点一定
在这个函数的图象上。
(2)在函数图象上的点A(x,y)中的x、y一定满足函
数的解析式。 1、函数图象的概念:
把一个函数的自变量x与对应的函数y的值分别作
为点的横坐标和纵坐标 , 在直角坐标系内描出它的对 应点 , 所有这些点组成的图形叫做该函数的图象. 3、“描点法”作函数图象的一般步骤:
(1)列表; (2)描点;(3)连线
6、函数的代数表达式与函数图象是紧密联系着的,“数”用“形”表示,由“形”想到“数”,这是我们数学学习中一个很重要的思想方法——数形结合。5、画函数图象时还应特别注意:需考虑自变量的取值范围。作业
1.必做题:作业本(2)及课本作业题A组。
2.选做题:课本作业题B、C组。考考你
已知直线y= -2x+4,它与x轴的交点为A,与y轴的交点为B.
(1).求A, B两点的坐标.
(2).求?AOB的面积. (O为坐标原点)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
