直角坐标系中的图形变换9复习)[下学期]
文档属性
| 名称 | 直角坐标系中的图形变换9复习)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 341.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-31 21:39:00 | ||
图片预览








文档简介
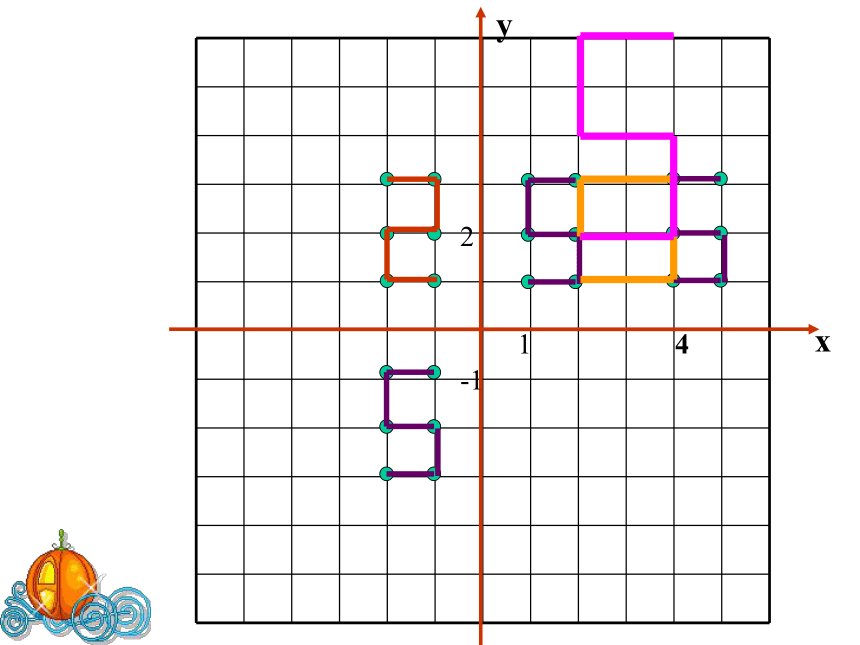
课件21张PPT。直角坐标系中的图形变换旋转变换直角坐标系中的图形变换相似变换轴对称变换直角坐标系中的图形变换轴对称变换直角坐标系中的图形变换轴对称变换平移变换直角坐标系中的图形变换相似变换旋转变换直角坐标系中的图形变换相似变换旋转变换直角坐标系中的图形变换在直角坐标系内,将坐标为(1,1),(2,1),(2,2),(1,2),(1,3),(2,3)的点依次连接起来,组成一个图形.(1)每个点的纵坐标不变,横坐标都加3,再将所得点用线依次连接起来,所得图案与原图案相比有什么变化?(2)纵坐标不变,横坐标乘以-1呢?(4)纵坐标不变,横坐标乘以2呢?(3)每个点的纵坐标、横坐标都乘以-1(5)每个点的纵坐标、横坐标都乘以2呢?你一定行!习中求进12-14如图,A、B两村在河的同旁,以河边为轴建立直角坐标系,则A、B两村对应的坐标分别为A(-1,1),B(2,5),现要在河边建一水泵站,分别直接向A、B两处供水,问水泵站P选在何处,可使得所用的水管最短?并求出点P的坐标.1-1A’P学以致用(1)判断△ ABC的形状如图,在平面直角坐标系中, △ ABC的三个顶点的坐标分别是
A(1,1),
B(3,2),
C(2,4).开拓思维(2)设P(a,b)是坐标平面内△ ABC上的任意一点.由P(a,b)到(a,2-b)表示一组怎样的图形变换?请在图中作出△ ABC经这组变换后所得的像.思考(3)若保持顶点A,C的位置不动,作关于顶点B的一个(或者一组)变换,使变换后的三角形仍是等腰直角三角形.请作出点B经变换后所得的像,并求出相应点的B的像的坐标.如图,平面直角坐标系中,△ABC为等边三角形,其中点A、B、C的坐标分别为(-3,-1)、(-3,-3)、(-3+ ,-2).现以轴为对称轴作△ABC的对称图形,得△A1B1C1,再以轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.(1)直接写出点C1、C2的坐标;勇攀高峰
(2)能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的度数;你若认为不能,请作出否定的回答(不必说明理由);
?(3)设当△ABC的位置发生变化时, △A2B2C2 、 △A1B1C1与△ ABC之间的对称关系始终保持不变.①当△向上平移多少个单位时, △A1B1C1与△A2B2C2完全重合?并直接写出此时点C的坐标;②将△ABC绕点顺时针旋转α? (0? α? 180),使△A1B1C1与△A2B2C2完全重合,此时α的值为多少?点C的坐标又是什么?
关于x轴对称,横坐标不变,纵坐标变为原来的相反数关于y轴对称,纵坐标不变,横坐标变为原来的相反数(a,b)(a,-b)(a,b)(-a,b)知识链接(1)左右平移时:
(a,b) 向右平移h个单位(a+h, b)(a,b) 向左平移h个单位(a-h, b)(2)上下平移时:
(a,b) 向上平移h个单位(a, b+h)向下平移h个单位(a, b -h )(a,b) 平移时的坐标变化知识链接横坐标不变,纵坐标乘以 a,意味着图像纵向扩大|a |倍;纵坐标不变,横坐标乘以a,意味着图像向扩大|a |倍;横坐标乘以a,纵坐标同时乘以b,意味着图像横向
扩大|a |倍,同时纵向扩大| b|倍;图形的相似变换,意味着图形点的横坐标与纵坐标同时乘以相同的数.知识链接 ?
A(1,1),
B(3,2),
C(2,4).开拓思维(2)设P(a,b)是坐标平面内△ ABC上的任意一点.由P(a,b)到(a,2-b)表示一组怎样的图形变换?请在图中作出△ ABC经这组变换后所得的像.思考(3)若保持顶点A,C的位置不动,作关于顶点B的一个(或者一组)变换,使变换后的三角形仍是等腰直角三角形.请作出点B经变换后所得的像,并求出相应点的B的像的坐标.如图,平面直角坐标系中,△ABC为等边三角形,其中点A、B、C的坐标分别为(-3,-1)、(-3,-3)、(-3+ ,-2).现以轴为对称轴作△ABC的对称图形,得△A1B1C1,再以轴为对称轴作△A1B1C1的对称图形,得△A2B2C2.(1)直接写出点C1、C2的坐标;勇攀高峰
(2)能否通过一次旋转将△ABC旋转到△A2B2C2的位置?你若认为能,请作出肯定的回答,并直接写出所旋转的度数;你若认为不能,请作出否定的回答(不必说明理由);
?(3)设当△ABC的位置发生变化时, △A2B2C2 、 △A1B1C1与△ ABC之间的对称关系始终保持不变.①当△向上平移多少个单位时, △A1B1C1与△A2B2C2完全重合?并直接写出此时点C的坐标;②将△ABC绕点顺时针旋转α? (0? α? 180),使△A1B1C1与△A2B2C2完全重合,此时α的值为多少?点C的坐标又是什么?
关于x轴对称,横坐标不变,纵坐标变为原来的相反数关于y轴对称,纵坐标不变,横坐标变为原来的相反数(a,b)(a,-b)(a,b)(-a,b)知识链接(1)左右平移时:
(a,b) 向右平移h个单位(a+h, b)(a,b) 向左平移h个单位(a-h, b)(2)上下平移时:
(a,b) 向上平移h个单位(a, b+h)向下平移h个单位(a, b -h )(a,b) 平移时的坐标变化知识链接横坐标不变,纵坐标乘以 a,意味着图像纵向扩大|a |倍;纵坐标不变,横坐标乘以a,意味着图像向扩大|a |倍;横坐标乘以a,纵坐标同时乘以b,意味着图像横向
扩大|a |倍,同时纵向扩大| b|倍;图形的相似变换,意味着图形点的横坐标与纵坐标同时乘以相同的数.知识链接 ?
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
