2.1 一元二次方程(1)[下学期]

课件13张PPT。
2.1 一元二次方程(一)列出下列问题中关于未知数x的方程:
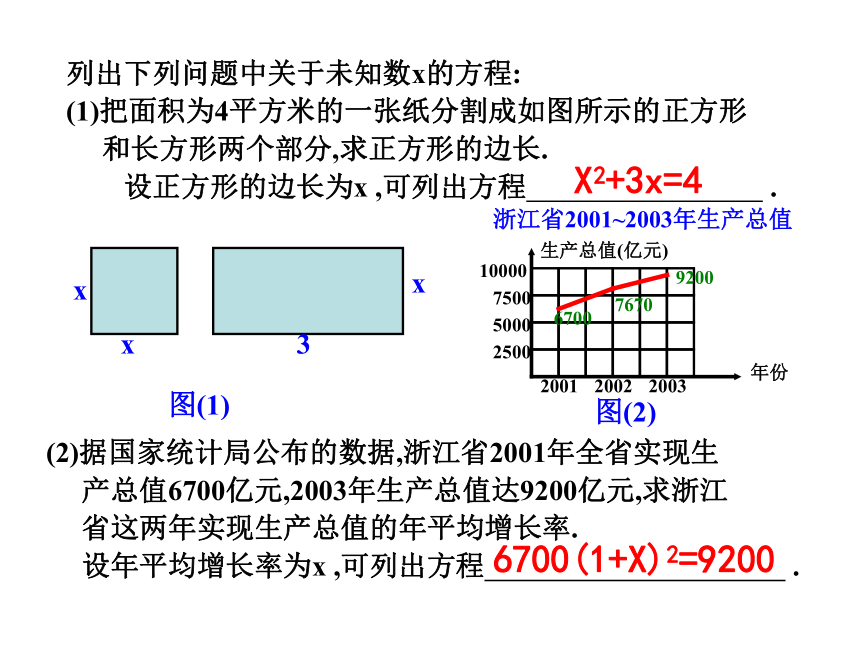
(1)把面积为4平方米的一张纸分割成如图所示的正方形
和长方形两个部分,求正方形的边长.
设正方形的边长为x ,可列出方程 .(2)据国家统计局公布的数据,浙江省2001年全省实现生
产总值6700亿元,2003年生产总值达9200亿元,求浙江
省这两年实现生产总值的年平均增长率.
设年平均增长率为x ,可列出方程 .图(1)图(2)浙江省2001~2003年生产总值生产总值(亿元)年份25005000750010000200120022003670076709200X2+3x=46700(1+X)2=9200观察上面所列的方程,说出这些方程与
一元一次方程的相同和不同之处. 未知数的最高次数是2次方程两边都是 ，只含有 ，并且

的方程叫做一元二次方程。一元二次方程的定义:思考：整式一个未知数X2 + 3x =4能使一元二次方程两边相等的未知数的值叫
一元二次方程的解(或根)6700(1+X)2=9200练一练1.下列方程属于一元二次方程的是( )A.x2+1=x(x+1) B.
C.(y-1)(y+2)=0 D.ax2+bx+c=02.判断下列各方程后面的两个数是
不是它的解,是的打‘‘ ’’.(1)x2-6x-7=0; (-1,7)(2)3x2+5x-2=0; ( )(3)2x2-3x+1=0; (3,1)(4) x2-4x+1=0.
( )C√√一元二次方程的一般形式ax２＋bx＋c＝０(a, b，c为常数, a≠０)a: 二次项系数b: 一次项系数．
c : 常数项 a≠０ax2+bx+c=0(a≠0)例1已知方程 x(3x-3)-2x(x-1)-2=0 , 指出该方程的二次项系数、一次项系数和常数项。说出二次项系数、一次项系数和常数项时,必须
将方程化为一般形式；把一元二次方程化为一
般形式时,通常按未知数的次数从高到低排列。解: x(3x-3)-2x(x-1)-2=0 去括号,得 3x2-3x-2x2+2x-2 =0 整理,得 x2-x-2=0 所以二次项系数为1,一次项系数为-1,常数项为-2. 把下列方程化为一元二次方程的形式，并写出它的二次项系数、一次项系数和常数项：比一比例2已知关于 x 的一元二次方程
mx2+m2=x2-2x+1的一个解是0,
求m的值.解: 将x=0代入方程,得m2=1,则m=±1 由于一元二次方程整理后是
(m-1)x2+2x+m2-1=0所以 m-1≠0 即m≠1 所以 m= -1 ax2+bx+c=0(a≠0)例31.关于x的方程 (k－3)x2 ＋ 2x－1＝0,当 k _______时，是一元二次方程．≠32.关于x的方程 (k2－1)x2 ＋ 2 (k－1) x ＋ 2k
＋ 2＝0, 当k 　　　时，是一元二次方程;
当 k 　　　 时，是一元一次方程．≠±1＝－13.若关于x的方程（m+1)x |m|+1 -2x+3m=0
是一元二次方程,求m的值。 1、已知关于x的一元二次方程x2+ax+a=0
的一个根是3，求a的值。 2、已知关于x的一元二次方程ax2+bx+c=0
的一个根是1，求a+b+c的值。 若a-b+c=0，你能通过观察,求出方程的一个根吗？3、构造一个一元二次方程，要求：
（1）常数项为零；（2）有一根为2。试一试解：设竹竿的长为x尺,则门的长 度为 尺,宽为 尺,依题意得方程： 从前有一天，一个醉汉拿着竹竿进屋，横拿竖拿都进不去，横着比门框宽４尺，竖着比门框高２尺，另一个醉汉教他沿着门的两个对角斜着拿竿，这个醉汉一试，不多不少刚好进去了．你知道竹竿有多长吗？请根据这一问题列出方程．(x－4)2＋ (x－2)2＝ x24尺2尺xx－4x－2(x－4)(x－2)用一用ax２＋bx＋c＝０(a, b，c为常数, a≠０) 2. 一元二次方程的一般形式 １．学习了什么是一元二次方程 3. 会用一元二次方程表示实际生活中 的数量关系
课堂小结祝新年快乐！
学业进步！