2022—2023学年浙教版数学八年级下册第五章特殊平行四边形 同步练习(无答案)
文档属性
| 名称 | 2022—2023学年浙教版数学八年级下册第五章特殊平行四边形 同步练习(无答案) | 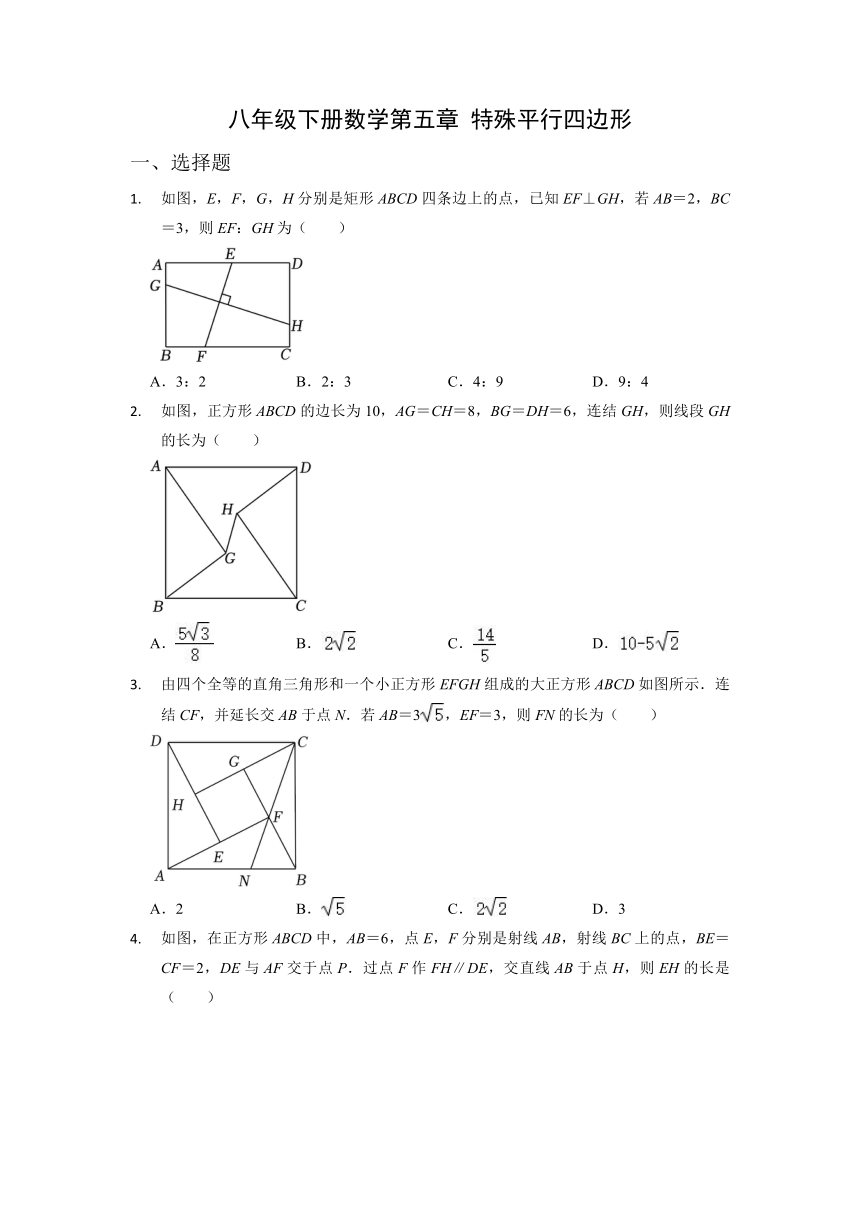 | |
| 格式 | docx | ||
| 文件大小 | 202.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 13:08:28 | ||
图片预览

文档简介
八年级下册数学第五章 特殊平行四边形
一、选择题
如图,E,F,G,H分别是矩形ABCD四条边上的点,已知EF⊥GH,若AB=2,BC=3,则EF:GH为( )
A.3:2 B.2:3 C.4:9 D.9:4
如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连结GH,则线段GH的长为( )
A. B. C. D.
由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结CF,并延长交AB于点N.若AB=3,EF=3,则FN的长为( )
A.2 B. C. D.3
如图,在正方形ABCD中,AB=6,点E,F分别是射线AB,射线BC上的点,BE=CF=2,DE与AF交于点P.过点F作FH∥DE,交直线AB于点H,则EH的长是( )
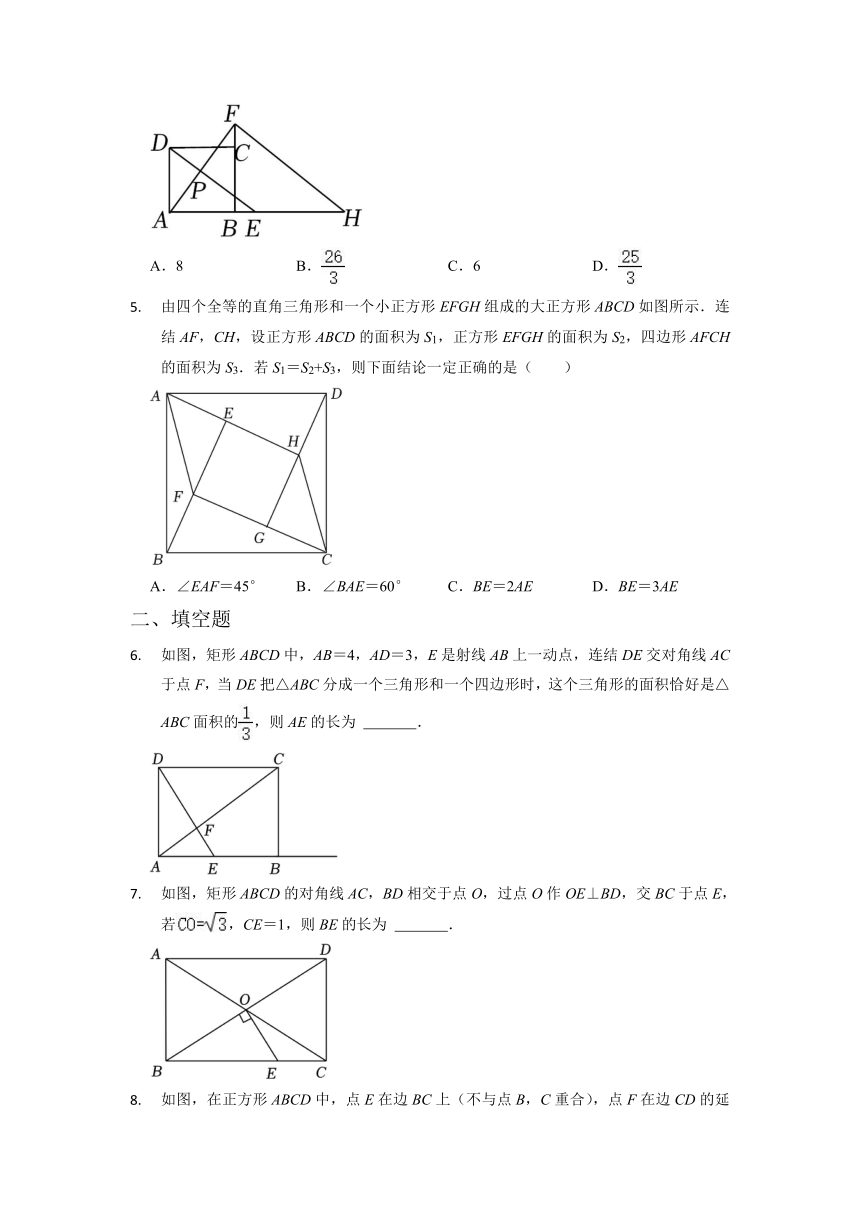
A.8 B. C.6 D.
由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结AF,CH,设正方形ABCD的面积为S1,正方形EFGH的面积为S2,四边形AFCH的面积为S3.若S1=S2+S3,则下面结论一定正确的是( )
A.∠EAF=45° B.∠BAE=60° C.BE=2AE D.BE=3AE
二、填空题
如图,矩形ABCD中,AB=4,AD=3,E是射线AB上一动点,连结DE交对角线AC于点F,当DE把△ABC分成一个三角形和一个四边形时,这个三角形的面积恰好是△ABC面积的,则AE的长为 .
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥BD,交BC于点E,若,CE=1,则BE的长为 .
如图,在正方形ABCD中,点E在边BC上(不与点B,C重合),点F在边CD的延长线上,DF=BE,连接EF交AD于点G,过点A作AN⊥EF于点M,交边CD于点N.若DN=2CN,BE=3.则CN= ,AM= .
如图,长方形EDFG的顶点E,F分则在正方形ABCD的边CD,DA上,点G在正方形内.若AF=1,CE=2,长方形EDFG的面积为s(s是正数),设ED+DF=m,用含s的代数式表示m2为 .
三、解答题
如图,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若CD=2,∠ABC=60°=2∠C,求AB的长.
如图,O是 ABCD对角线的交点,BE⊥OC于点E,延长BE至点F,使EF=BE,连结DF.
(1)求证:∠F=90°.
(2)当 ABCD为矩形,AC=6,BF=2时,求DF,CE的长.
在正方形ABCD中,点E在AD边上(不与点A,点D重合).连接BE,作AG⊥BE于点F,交CD边于点G,连接CF.
(1)求证:BE=AG.
(2)若点E是D边的中点,AD=10.
①分别求AF,BF的长.
②求证:CB=CF.
如图,在△ABC中,BA=BC,BD平分∠ABC交AC于点D,点E在线段BD上,点F在BD的延长线上,且DE=DF,连接AE,CE,AF,CF.
(1)求证:四边形AECF是菱形;
(2)若BA⊥AF,AD=4,BC=4,求BD和AE的长.
如图,四边形ABCD是正方形,△ABE是等腰三角形,AB=AE,∠BAE=θ(0°<θ<90°).连接DE,过B作BF⊥DE于F,连接AF,CF.
(1)若θ=60°,求∠BED的度数;
(2)当θ变化时,∠BED的大小会发生变化吗?请说明理由;
(3)试用等式表示线段DE与CF之间的数量关系,并证明.
一、选择题
如图,E,F,G,H分别是矩形ABCD四条边上的点,已知EF⊥GH,若AB=2,BC=3,则EF:GH为( )
A.3:2 B.2:3 C.4:9 D.9:4
如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连结GH,则线段GH的长为( )
A. B. C. D.
由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结CF,并延长交AB于点N.若AB=3,EF=3,则FN的长为( )
A.2 B. C. D.3
如图,在正方形ABCD中,AB=6,点E,F分别是射线AB,射线BC上的点,BE=CF=2,DE与AF交于点P.过点F作FH∥DE,交直线AB于点H,则EH的长是( )
A.8 B. C.6 D.
由四个全等的直角三角形和一个小正方形EFGH组成的大正方形ABCD如图所示.连结AF,CH,设正方形ABCD的面积为S1,正方形EFGH的面积为S2,四边形AFCH的面积为S3.若S1=S2+S3,则下面结论一定正确的是( )
A.∠EAF=45° B.∠BAE=60° C.BE=2AE D.BE=3AE
二、填空题
如图,矩形ABCD中,AB=4,AD=3,E是射线AB上一动点,连结DE交对角线AC于点F,当DE把△ABC分成一个三角形和一个四边形时,这个三角形的面积恰好是△ABC面积的,则AE的长为 .
如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥BD,交BC于点E,若,CE=1,则BE的长为 .
如图,在正方形ABCD中,点E在边BC上(不与点B,C重合),点F在边CD的延长线上,DF=BE,连接EF交AD于点G,过点A作AN⊥EF于点M,交边CD于点N.若DN=2CN,BE=3.则CN= ,AM= .
如图,长方形EDFG的顶点E,F分则在正方形ABCD的边CD,DA上,点G在正方形内.若AF=1,CE=2,长方形EDFG的面积为s(s是正数),设ED+DF=m,用含s的代数式表示m2为 .
三、解答题
如图,在四边形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若CD=2,∠ABC=60°=2∠C,求AB的长.
如图,O是 ABCD对角线的交点,BE⊥OC于点E,延长BE至点F,使EF=BE,连结DF.
(1)求证:∠F=90°.
(2)当 ABCD为矩形,AC=6,BF=2时,求DF,CE的长.
在正方形ABCD中,点E在AD边上(不与点A,点D重合).连接BE,作AG⊥BE于点F,交CD边于点G,连接CF.
(1)求证:BE=AG.
(2)若点E是D边的中点,AD=10.
①分别求AF,BF的长.
②求证:CB=CF.
如图,在△ABC中,BA=BC,BD平分∠ABC交AC于点D,点E在线段BD上,点F在BD的延长线上,且DE=DF,连接AE,CE,AF,CF.
(1)求证:四边形AECF是菱形;
(2)若BA⊥AF,AD=4,BC=4,求BD和AE的长.
如图,四边形ABCD是正方形,△ABE是等腰三角形,AB=AE,∠BAE=θ(0°<θ<90°).连接DE,过B作BF⊥DE于F,连接AF,CF.
(1)若θ=60°,求∠BED的度数;
(2)当θ变化时,∠BED的大小会发生变化吗?请说明理由;
(3)试用等式表示线段DE与CF之间的数量关系,并证明.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
