2022-2023学浙教版数学八年级下册第五章特殊平行四边形精练(无答案)
文档属性
| 名称 | 2022-2023学浙教版数学八年级下册第五章特殊平行四边形精练(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 314.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-11 00:00:00 | ||
图片预览


文档简介
2023浙教版数学八年级下册第五章精练
一、选择题
如图,在边长为4的正方形ABCD中,点E、点F分别是BC、AB上的点,连接DE、DF、EF,满足∠DEF=∠DEC.若AF=1,则EF的长为( )
A.2.4 B.3.4 C. D.
如图,BD是正方形ABCD的对角线,在BD上截取DE=DC,在CB延长线上取一点F,连接EF,AF,且EF=EC.下列四个结论:①BF=BE;②∠BAF=∠BCE;③∠AFE=45°;④连接AE,则S四边形AECD=2S四边形AFBE.其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
已知菱形ABCD,E、F是动点,边长为5,BE=AF,∠BAD=120°,则下列命题中正确的是( )
①△BEC≌△AFC;
②△ECF为等边三角形;
③△ECF的边长最小值为3;
④若AF=2,则S△FGC=S△EGC.
A.①② B.①③ C.①②④ D.①②③
如图,在正方形ABCD中,点E是边BC上一点,且AB=3BE.过点B作BF⊥AE,交边CD于点F.以C为圆心,CF长为半径画圆,交边BC于点G,连接DG,交BF于点H.则DH:HG=( )
A.10:3 B.3:1 C.8:3 D.5:3
如图, ABCD中,点E、F分别在边AD、BC上,点G、H在边BD上,且AE=CF,BG=DH,关于四边形EGFH,下列说法正确的个数是( )
①四边形EGFH一定是平行四边形且有无数个;
②四边形EGFH可以是矩形且有无数个;
③四边形EGFH可以是菱形且有无数个;
④四边形EGFH可以是正方形且有无数个.
A.1个 B.2个 C.3个 D.4个
如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
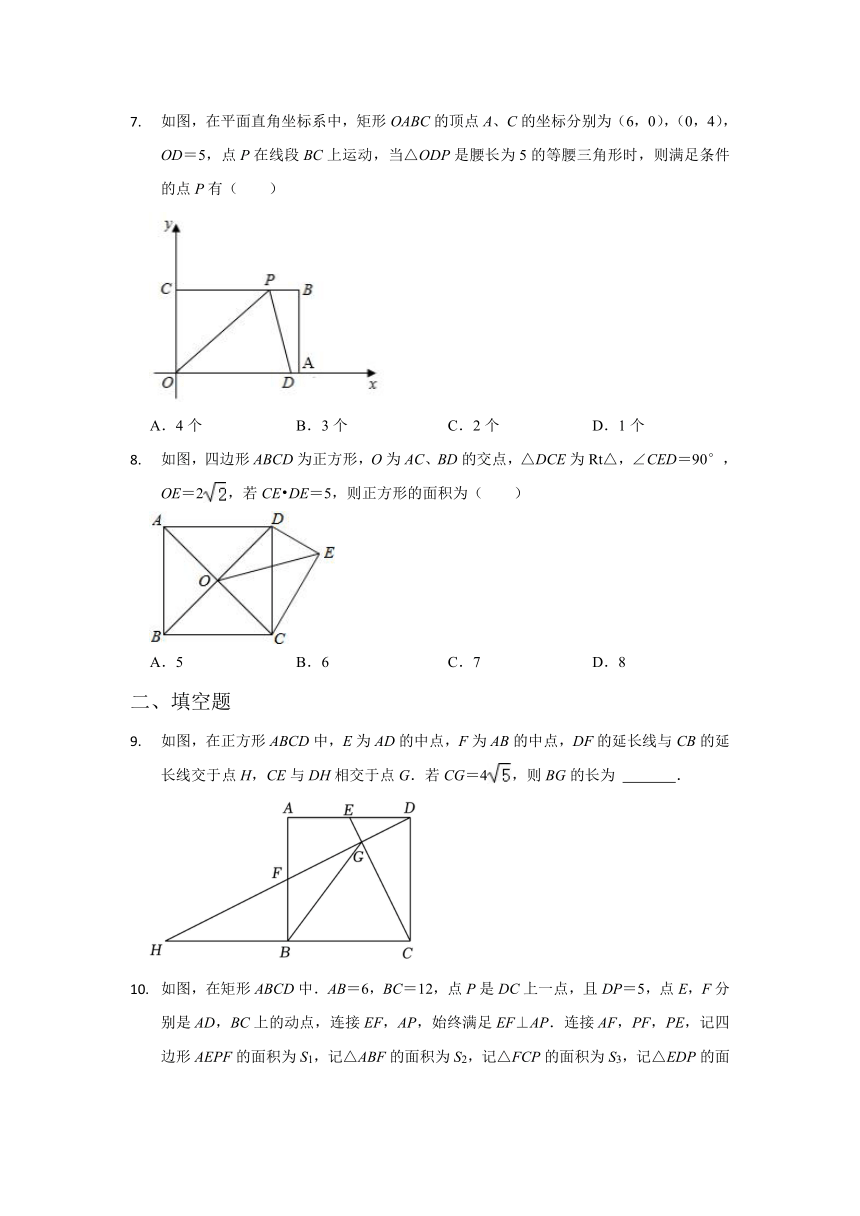
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0),(0,4),OD=5,点P在线段BC上运动,当△ODP是腰长为5的等腰三角形时,则满足条件的点P有( )
A.4个 B.3个 C.2个 D.1个
如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
二、填空题
如图,在正方形ABCD中,E为AD的中点,F为AB的中点,DF的延长线与CB的延长线交于点H,CE与DH相交于点G.若CG=4,则BG的长为 .
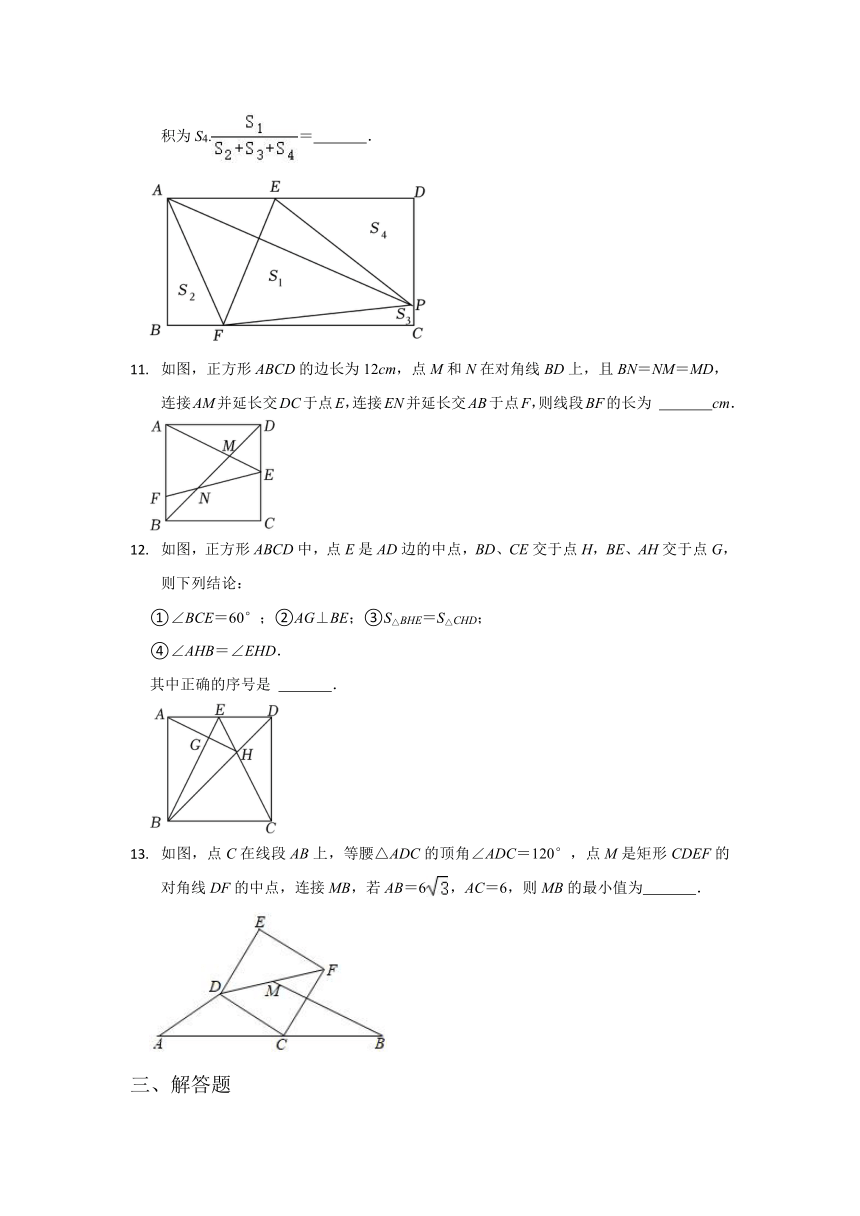
如图,在矩形ABCD中.AB=6,BC=12,点P是DC上一点,且DP=5,点E,F分别是AD,BC上的动点,连接EF,AP,始终满足EF⊥AP.连接AF,PF,PE,记四边形AEPF的面积为S1,记△ABF的面积为S2,记△FCP的面积为S3,记△EDP的面积为S4.= .
如图,正方形ABCD的边长为12cm,点M和N在对角线BD上,且BN=NM=MD,连接AM并延长交DC于点E,连接EN并延长交AB于点F,则线段BF的长为 cm.
如图,正方形ABCD中,点E是AD边的中点,BD、CE交于点H,BE、AH交于点G,则下列结论:
①∠BCE=60°;②AG⊥BE;③S△BHE=S△CHD;
④∠AHB=∠EHD.
其中正确的序号是 .
如图,点C在线段AB上,等腰△ADC的顶角∠ADC=120°,点M是矩形CDEF的对角线DF的中点,连接MB,若AB=6,AC=6,则MB的最小值为 .
三、解答题
如图,正方形ABCD的对角线AC,BD相交于点O,E是BC边上一点,连接AE交BD于点M,过点B作BF⊥AE于点P,交AC于点G,交CD于点F.
(1)求证:△ABE≌△BCF;
(2)求证:OM=OG;
(3)若AE平分∠BAC,求证:BM2=2OM2.
如图,正方形ABCD,点E,F是对角线AC上的两点,∠EBF=45°,连接BE,BF,△ABE和△GBE关于直线BE对称.点G在BD上,连接FG.
(1)求∠FBC的度数;
(2)如备用图,延长BF交CD于点H,连接HG.
①求证:四边形GHCF是菱形;
②求的值.
如图,在 ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=2,BF=2,CE=1,求 ABCD的面积.
在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE= ,EF=
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
(1)求证:∠BAG=∠CBF;
(2)求证:AG=FG;
(3)若GF=2BG,CF=,求AB的长.
如图1,已知在四边形ABCD中,AD∥BC,AB∥CD,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.
(1)求证:四边形ABFE是菱形;
(2)若∠ABC=90°,如图2所示:
①求证:∠ADO=∠BCO;
②若∠EOD=15°,AE=1,求OC的长.
一、选择题
如图,在边长为4的正方形ABCD中,点E、点F分别是BC、AB上的点,连接DE、DF、EF,满足∠DEF=∠DEC.若AF=1,则EF的长为( )
A.2.4 B.3.4 C. D.
如图,BD是正方形ABCD的对角线,在BD上截取DE=DC,在CB延长线上取一点F,连接EF,AF,且EF=EC.下列四个结论:①BF=BE;②∠BAF=∠BCE;③∠AFE=45°;④连接AE,则S四边形AECD=2S四边形AFBE.其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
已知菱形ABCD,E、F是动点,边长为5,BE=AF,∠BAD=120°,则下列命题中正确的是( )
①△BEC≌△AFC;
②△ECF为等边三角形;
③△ECF的边长最小值为3;
④若AF=2,则S△FGC=S△EGC.
A.①② B.①③ C.①②④ D.①②③
如图,在正方形ABCD中,点E是边BC上一点,且AB=3BE.过点B作BF⊥AE,交边CD于点F.以C为圆心,CF长为半径画圆,交边BC于点G,连接DG,交BF于点H.则DH:HG=( )
A.10:3 B.3:1 C.8:3 D.5:3
如图, ABCD中,点E、F分别在边AD、BC上,点G、H在边BD上,且AE=CF,BG=DH,关于四边形EGFH,下列说法正确的个数是( )
①四边形EGFH一定是平行四边形且有无数个;
②四边形EGFH可以是矩形且有无数个;
③四边形EGFH可以是菱形且有无数个;
④四边形EGFH可以是正方形且有无数个.
A.1个 B.2个 C.3个 D.4个
如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0),(0,4),OD=5,点P在线段BC上运动,当△ODP是腰长为5的等腰三角形时,则满足条件的点P有( )
A.4个 B.3个 C.2个 D.1个
如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE DE=5,则正方形的面积为( )
A.5 B.6 C.7 D.8
二、填空题
如图,在正方形ABCD中,E为AD的中点,F为AB的中点,DF的延长线与CB的延长线交于点H,CE与DH相交于点G.若CG=4,则BG的长为 .
如图,在矩形ABCD中.AB=6,BC=12,点P是DC上一点,且DP=5,点E,F分别是AD,BC上的动点,连接EF,AP,始终满足EF⊥AP.连接AF,PF,PE,记四边形AEPF的面积为S1,记△ABF的面积为S2,记△FCP的面积为S3,记△EDP的面积为S4.= .
如图,正方形ABCD的边长为12cm,点M和N在对角线BD上,且BN=NM=MD,连接AM并延长交DC于点E,连接EN并延长交AB于点F,则线段BF的长为 cm.
如图,正方形ABCD中,点E是AD边的中点,BD、CE交于点H,BE、AH交于点G,则下列结论:
①∠BCE=60°;②AG⊥BE;③S△BHE=S△CHD;
④∠AHB=∠EHD.
其中正确的序号是 .
如图,点C在线段AB上,等腰△ADC的顶角∠ADC=120°,点M是矩形CDEF的对角线DF的中点,连接MB,若AB=6,AC=6,则MB的最小值为 .
三、解答题
如图,正方形ABCD的对角线AC,BD相交于点O,E是BC边上一点,连接AE交BD于点M,过点B作BF⊥AE于点P,交AC于点G,交CD于点F.
(1)求证:△ABE≌△BCF;
(2)求证:OM=OG;
(3)若AE平分∠BAC,求证:BM2=2OM2.
如图,正方形ABCD,点E,F是对角线AC上的两点,∠EBF=45°,连接BE,BF,△ABE和△GBE关于直线BE对称.点G在BD上,连接FG.
(1)求∠FBC的度数;
(2)如备用图,延长BF交CD于点H,连接HG.
①求证:四边形GHCF是菱形;
②求的值.
如图,在 ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=2,BF=2,CE=1,求 ABCD的面积.
在矩形ABCD中,AB=3,BC=4,E,F是对角线AC上的两个动点,分别从A,C同时出发相向而行,速度均为1cm/s,运动时间为t秒,0≤t≤5.
(1)AE= ,EF=
(2)若G,H分别是AB,DC中点,求证:四边形EGFH是平行四边形.
(3)在(2)条件下,当t为何值时,四边形EGFH为矩形.
如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
(1)求证:∠BAG=∠CBF;
(2)求证:AG=FG;
(3)若GF=2BG,CF=,求AB的长.
如图1,已知在四边形ABCD中,AD∥BC,AB∥CD,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.
(1)求证:四边形ABFE是菱形;
(2)若∠ABC=90°,如图2所示:
①求证:∠ADO=∠BCO;
②若∠EOD=15°,AE=1,求OC的长.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
