有理数的复习[上学期]

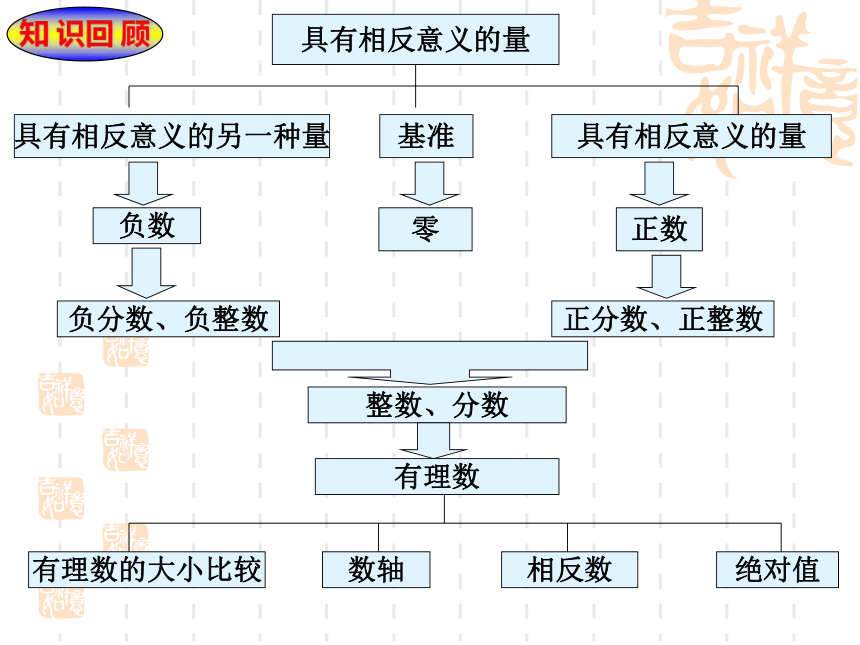
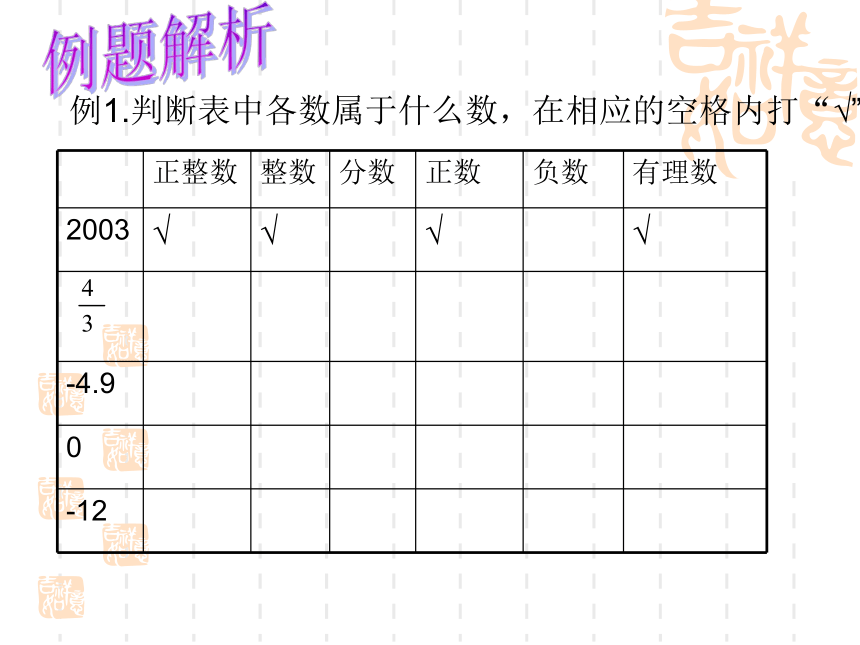
课件14张PPT。第一章 从自然数到有理数复习煤山镇中 章新金具有相反意义的量具有相反意义的另一种量具有相反意义的量基准正数零负数负分数、负整数正分数、正整数整数、分数有理数有理数的大小比较数轴相反数绝对值知 识回 顾例1.判断表中各数属于什么数，在相应的空格内打“√”例题解析例2 . 如图，两个圈内分别表示所有正数组成的正数集合和所有分数组成的分数集合，请写出3个分别满足下列条件的数：①属于正数集合，但不属于分数集合的数；
②属于分数集合，但不属于正数集合的数；
③既属于正数集合，又属于分数集合的数
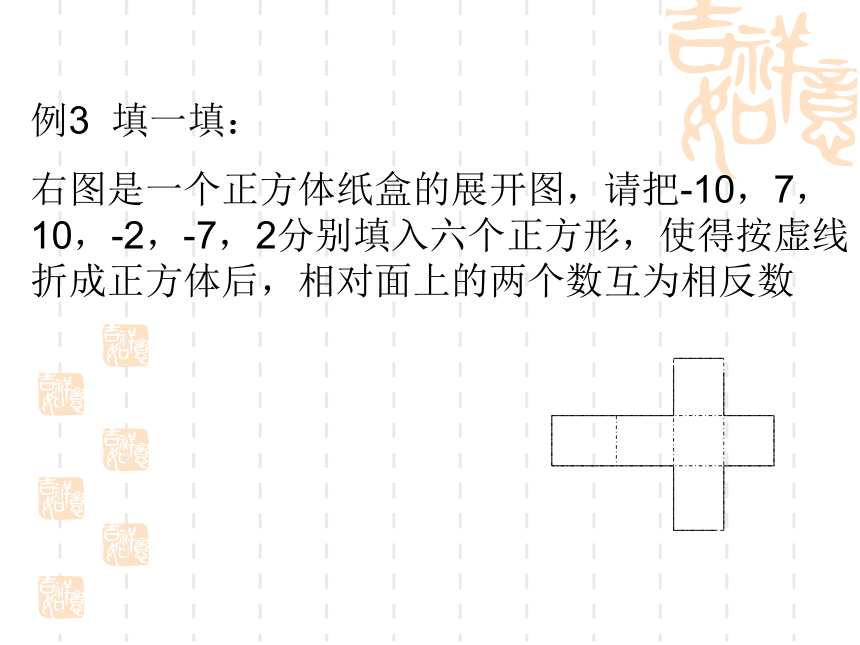
将它们分别填入图中适当的位置，你能说出这两个圈重叠部分表示什么数吗？例3 填一填：
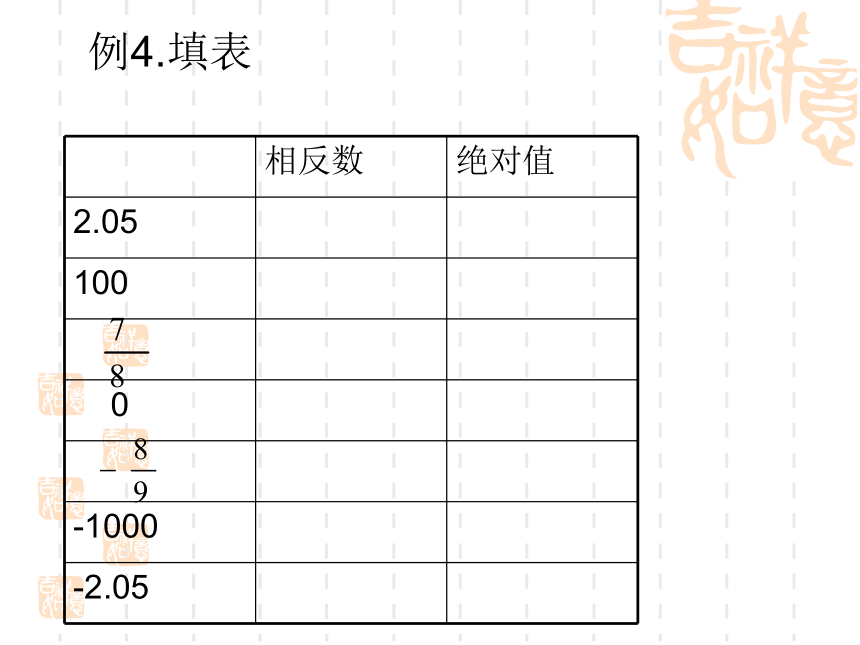
右图是一个正方体纸盒的展开图，请把-10，7，10，-2，-7，2分别填入六个正方形，使得按虚线折成正方体后，相对面上的两个数互为相反数例4.填表例5. 回答下列问题：⑴一个数的绝对值是它本身，这个数是什么？
⑵一个数的绝对值是它的相反数，这个数是什么数？
⑶一个数的绝对值一定是正数吗？
⑷一个数的绝对值不可能是负数，对吗？
⑸绝对值是同一个正数的数有两个，它们互为相反数，这句话对吗？1、在数轴上表示下列各数，并用“＜”号连接：
3，-3，2，-2.5，1.5，0.
2、比较下列各对数的大小：
（1）-3.6______0；
（2）0.7______4+1/3；
（3）-6.3______3.6；
（4）-56______-566；
（5）-0.01______-0.1；
（6）17+2/3______0.
3、比较-1/3，-0.3和-2/3的大小，下列用不等号连接正确的是（ ）
A、-1/3＜-0.3＜-2/3 B、-1/3＞-2/3＞-0.3
C、-0.3＞-1/3＞-2/3 D、-0.3＞-2/3＞-1/3
＜＜C-3＜-2.5 ＜0 ＜1.5 ＜2 ＜3＜＞ ＞ ＞ 例6.比较有理数大小练习一 请你回答下列问题：
⑴有没有最大的有理数，有没有最小的有理数，为什么？
⑵有没有绝对值最小的有理数？若有，请把它写出来
⑶大于-1.5且小于4.2的整数有_____个，它们分别是____;
⑷若a>0,b<0,a<|b|,则你能比较a,b,-a,-b这四个数的大小吗?A组
1、填空：
（1）若射击比赛排名退步3名记为-3名，则进步5名记为______名；
（3）如果+13%表示增加13%，那么-11%表示_____________；
（4）飞机上升-150米，实际上飞机_________米；
2、在有理数中，最小的正整数是________，最大的负整数是________，绝对值最小的数是__________.
3、绝对值等于3的数是_________，绝对值等于4.6的负数是_____.
4、在数轴上，点A表示的有理数是-2，点B与点A的距离为4个单位长度，点B表示的有理数是__________.
5、下列两个数中，互为相反数的是（ ）
A、-1/2和0.2 B、1/3和-0.333 C、-2.25和+2.25 D、5和-(-5)
+5减少11%下降1501-10+3和-3-4.62或-6C当堂练习 6、若甲、乙两数在数轴上的对应点如图所示，则下列结论正 确的是（ ）
A、甲数大于乙数的绝对值 B、甲数小于乙数
C、甲数的绝对值大于乙数的绝对值
D、甲数的绝对值小于乙数的绝对值
7、小于 的非负整数有（ ）
A、6个 B、3个 C、4个 D、5个
8、把下列各数填入相应的括号内：
4.33, -1/2, 0, -3/7, 6, -5.42, 2/9, -55, 40%, -0.2.
正数：{ }；
负数：{ }；
整数：{ }；
分数：{ }.DA4.33, 6, 2/9, 40%-1/2, -3/7, -5.42, -55, -0.20, 6, -554.33, -1/2, -3/7, -5.42, 2/9, 40%, -0.2B组
9、绝对值小于4.9的整数有（ ）
A、6个 B、7个 C、8个 D、9个
10、在数轴上，点A和点B所表示的有理数分别为-4和2.5，则点A到点B的距离为_______.
11、下列判断不正确的是（ ）
A、一个正数的绝对值一定是正数；
B、一个数的绝对值等于它的相反数，这个数不是正数；
C、任何有理数的绝对值都不是负数；
D、任何有理数的绝对值都是正数.
D6.5D12、写出所有适合下列条件的数：
（1）小于3的正整数；
（2）大于-5的负整数；
（3）大于-2且不大于3的整数；
（4）绝对值大于3，不大于6的负整数.1, 2-4, -3, -2, -1-1, 0, 1, 2, 3-4, -5, -6探索思考:
　　点p从数轴上的原点出发，先向右移动１个单位，再向左移动２个单位，然后向右移动３个单位，再向左移动４个单位．求：
⑴点 p共移动了多少个单位长度；
⑵终止时，点p对应的数是多少？课堂小结:
1、进一步理解并运用有理数、数轴、相反数、绝对值等概念。
2、解决具体问题时应灵活应用知识。
3、领会数形结合的数学思想.