3.2 中位数和众数 同步练习（含答案）

中小学教育资源及组卷应用平台
浙教版（2012）八年级数学下册 同步练习
3.2中 位 数 和 众 数
一、选择题
1．某位同学近五次的数学随堂测试成绩（单位：分）分别为：95，89，95，98，94，则这组数据的众数是 （ ）
A．89 B．94 C．95 D．98
2．已知一组数据：这组数据的平均数和中位数分别是 （ ）
A．14，15 B．14，13 C．15，14 D．15，15
3．抢微信红包成为节日期间人们最喜欢的活动之一．对某单位50名员工在春节期间所抢的红包金额进行统计，并绘制成了如下统计图．根据如图提供的信息，红包金额的众数和中位数分别是 （ ）
A．30，30 B．30，20 C．40，40 D．30，40
4．某中学运动会上，有名运动员参加了米半决赛，按成绩取前8名进入决赛，小亮知道了自己的成绩，也知道名选手的成绩各不相同，要判断自己能否进入决赛，还要了解全部成绩的 （ ）
A．平均数 B．众数 C．中位数 D．方差
5．为振兴乡村经济，在某农产品网络销售中实行目标管理，根据目标完成的情况对销售员给予适当的奖励，下图是统计了名销售员某月的销售额（单位：万元）绘制的不完整的条形统计图，以下结论正确的是 （ ）
A．有3人销售额是4万元 B．平均月销售额是6万元
C．中位数是5万元 D．众数是3万元
二、填空题
6．已知一组数据，，，，的众数是，则的值是_______．
7．若一组数据：，，，，，的中位数是，那么的值是___________．
8．某品牌专卖店月份销售了双运动鞋，其尺码和数量统计如下表：
尺码 38 39 40 41 42
数量 2 4 5 6 3
这双运动鞋尺码的众数是______．
9．一组数据1，2，5，3，a的平均数是3，则中位数是_______．
10．已知一组数据的中位数是，那么x的值等于_____．
三、解答题
11．某鞋厂为了了解初中学生穿鞋的尺码情况，对某中学八年级（1）班的20名男生进行了调查，结果如图所示．
（1）写出这20个数据的平均数、中位数、众数；
（2）在平均数、中位数和众数中，鞋厂最感兴趣的是哪一个？
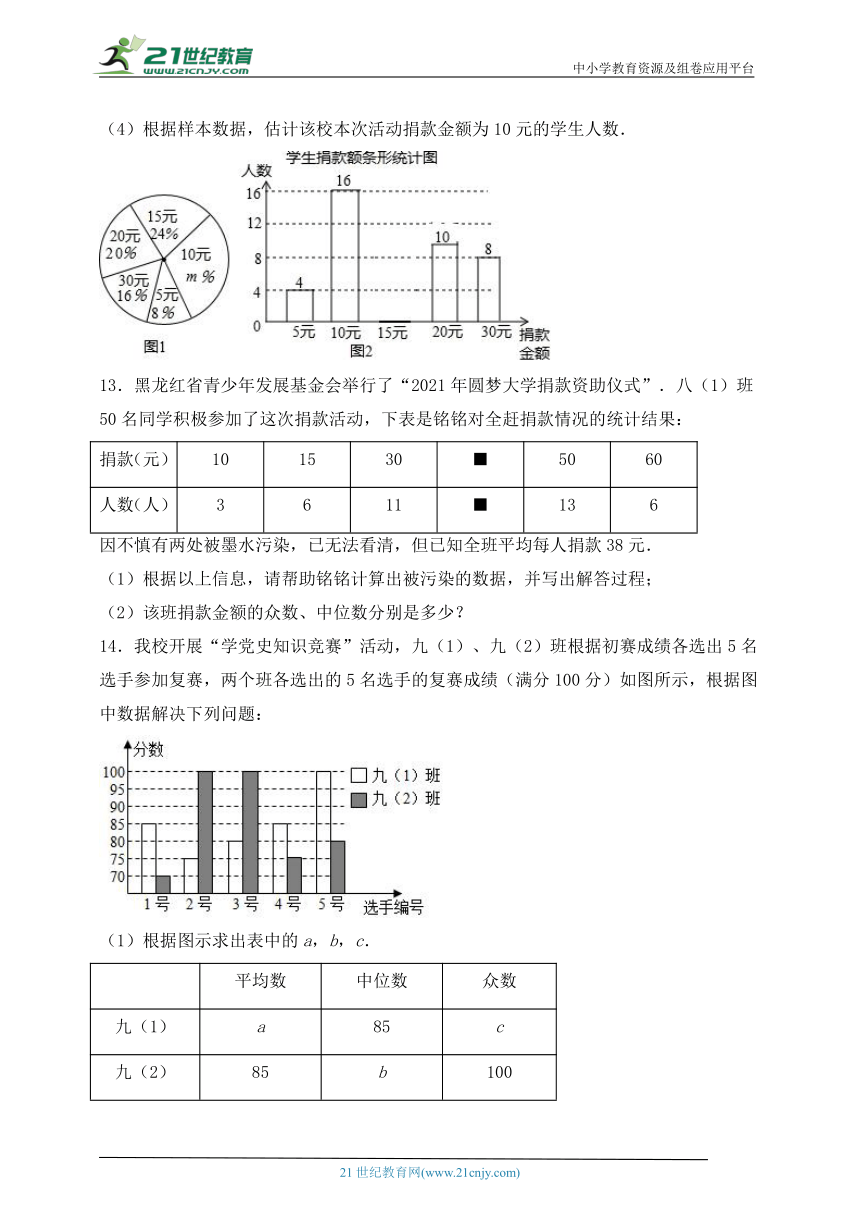
12．我校学生会在三月初组织给昆明市盲哑学校捐款献爱心，学生会向全校4500名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图1和图2，请根据相关信息，解答下列问题：
（1）本次接受随机抽样调查的学生人数为______人，图1中的值是______．
（2）补全条形统计图．
（3）求本次调查获取的样本数据的平均数是______元，众数是____元，中位数是___元；
（4）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．
13．黑龙红省青少年发展基金会举行了“2021年圆梦大学捐款资助仪式”．八（1）班50名同学积极参加了这次捐款活动，下表是铭铭对全赶捐款情况的统计结果：
捐款（元） 10 15 30 ■ 50 60
人数（人） 3 6 11 ■ 13 6
因不慎有两处被墨水污染，已无法看清，但已知全班平均每人捐款38元．
（1）根据以上信息，请帮助铭铭计算出被污染的数据，并写出解答过程；
（2）该班捐款金额的众数、中位数分别是多少？
14．我校开展“学党史知识竞赛”活动，九（1）、九（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分100分）如图所示，根据图中数据解决下列问题：
（1）根据图示求出表中的a，b，c．
平均数 中位数 众数
九（1） a 85 c
九（2） 85 b 100
_________，__________，__________．
（2）请你帮小明同学分析哪个班级的复赛成绩较好？
15．为了解本学期全校学生阅读课外书的情况，第一次随机抽查24名学生阅读课外书的册数，情况统计如下表，请回答下列问题．
册数 1 2 3 4
人数 5 m 6 4
(1)m=______；
(2)第一次抽查中，人均读书______册，阅读课外书册数的中位数是______册；
(3)第二次又随机抽查了几位同学，其中最少的读了3册，将其与第一次抽查的数据合并后，发现阅读课外书册数的中位数没发生改变，则第二次最多抽查了______人．
参考答案：
1．C
【分析】根据众数的概念逐一分析即可．
【解析】解：数据中出现次数最多的数据是分，
∴这组数据的众数是分，
故选C．
【点睛】本题主要考查众数，求一组数据的众数的方法：找出出现次数最多的那个数据，此时众数就是这个数据．
2．A
【分析】根据平均数的计算公式和中位数的定义分别进行解答即可．
【解析】解：这组数据的平均数是：；
把这组数据从小到大排列为，最中间的数是，则中位数是；
故应选：A．
【点睛】此题考查了平均数和中位数，掌握平均数的计算公式和中位数的定义是本题的关键．
3．C
【分析】根据众数和中位数的定义求解即可．
【解析】解：∵红包金额为40元的人数最多，有19人，
∴众数是40元；
∵50个数据从小到大排列，第25、26位置的数都为40，
∴中位数为元，
故选：C．
【点睛】本题考查众数和中位数，理解众数是一组数据中出现次数最多的数据，中位数是一组数据从小到大（或从大到小）重新排列后，若数据是奇数个，则中位数是最中间的那个数，如果数据是偶数个，则中位数是最中间两个数的平均数，注意先进行排序．
4．C
【分析】平均数代表数据的平均水平，众数表示数据中出现频数最多的次数，方差代表稳定性，中位数代表一组数据的中间值；有名运动员参加了米半决赛，按成绩取前8名进入决赛，要判断自己能否进入决赛，只需要和第8名的成绩作比较即可，第8名的成绩即为中位数．
【解析】解：要判断自己能否进入决赛，还要了解全部成绩的中位数即可，
故选：C．
【点睛】本题考查了平均数、众数、中位数和方差的意义；掌握中位数的意义是解题的关键．
5．C
【分析】根据条形统计图逐个判断即可得到答案；
【解析】解：由条形统计图可得，
销售额是4万元的人有：（人），故A选项错误；
平均月销售额是：（万元），故B选项错误；
∵，∴中位数落在5万元上，故C正确；
4万元有4人，故众数应该是4万元，
故选C．
【点睛】本题考查条形统计图，解题额关键是看懂条形统计图中数据，根据数据进行判断求解．
6．6
【分析】根据众数的定义，即可求解．
【解析】解：∵数据，，，，的众数是，
∴，
故答案为：6
【点睛】本题主要考查了众数，熟练掌握一组数据中，出现次数最多的数是众数是解题的关键．
7．
【分析】根据中位数的定义，将数列排序后，中间的数即为中位数，当数列中有奇数个数时，中间的数为中位数，当数列中有偶数个数时，中间两个数的一半为中位数，由此即可求解．
【解析】解：数列排序为：，，，， ，，
当时，数列为，，，，， ， 则中位数是，不符合题意；
当时，数列为，， ，，， ， 则中位数是，不符合题意；
当时，数列为，，， ，， ， 则中位数是，
∴，不符合题意；
当时，数列为，，，， ， ， 则中位数是，
∴，符合题意；
当时，数列为，，，，， ， 则中位数是，不符合题意；
当时，数列为，，，，，， 则中位数是，不符合题意；
故答案为：．
【点睛】本题主要考查中位数的确定方法，掌握中位数的定义是解题的关键．
8．
【分析】根据众数的定义：一组数据中出现次数最多的数据叫做这组数据的众数，故数量最多的尺码即是答案．
【解析】∵尺码，数量；尺码，数量；尺码，数量；尺码，数量；尺码，数量
∴
∴尺码是这双运动鞋尺码的众数
故答案为：．
【点睛】本题考查众数的定义，数量掌握众数的定义是解题的关键．
9．3
【分析】先根据平均数是3，求出a的值，然后根据中位数的定义求出结果即可．
【解析】解：根据题意，1，2，5，3，a的平均数是3，
，
解得，，
将这组数据从小到大排列为：1，2，3，4，5，
最中间的数是3，则这组数据的中位数是3．
故答案为：3．
【点睛】本题主要考查了平均数和中位数，解题的关键是根据平均数的定义求出，并熟练掌握中位数的定义．
10．
【分析】中位数是，这组数据有6个，是偶数个，所以就是最中间的两个数的平均数；再把这组数据按从小到大的顺序排一排，都比中位数小，所以x排在的后面，进而求得x的值．
【解析】解：根据题意，x的位置按从小到大排列只可能是：
根据中位数是得：．
解得．
故答案为：．
【点睛】本题考查了中位数的概念，关键是依据中位数，对数据排序，确定x的位置．
11．（1）平均数为39.1码，中位数为39码，众数为40码；（2）鞋厂最感兴趣的是众数
【分析】（1）根据平均数、众数与中位数的定义求解分析．40出现的次数最多为众数，第10、11个数的平均数为中位数．
（2）鞋厂最感兴趣的是使用的人数，即众数．
【解析】解：（1）平均数＝（37×3＋38×4＋39×4＋40×7＋41×1＋42×1）÷20＝39.1．
观察图表可知：有7人的鞋号为40，人数最多，即众数是40；
中位数是第10、11人的平均数，（39+39）÷2＝39，
故答案为：平均数为39.1码，中位数为39码，众数为40码；
（2）鞋厂最感兴趣的是使用的人数，即众数，
故答案为：鞋厂最感兴趣的是众数．
【点睛】本题考查平均数，众数与中位数．中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数．众数是数据中出现最多的一个数．正确理解中位数、众数及平均数的概念，是解决本题的关键．
12．（1）50、32；（2）补图见解析，（3）16元，10元，15元；（4）1440人．
【分析】（1）由5元的人数及其所占百分比可得总人数，用10元人数除以总人数可得m的值；
（2）总人数乘以15元对应百分比可得其人数，据此可补全图形；
（3）根据公式和定义可求样本数据的平均数、众数和中位数；
（4）根据统计图中的数据可以估计该校本次活动捐款金额为10元的学生人数．
【解析】解：（1）本次接受随机抽样调查的学生人数为4÷8%＝50人，
∵×100%＝32%，
∴m＝32，
故答案为：50、32；
（2）15元的人数为50×24%＝12（人），
补全图形如下：
（3）本次调查获取的样本数据的平均数是：×（4×5+16×10+12×15+10×20+8×30）＝16（元），
本次调查获取的样本数据中，10元出现的次数最多，众数是10元，
将数据从小到大排列，位于中间位置的两个数据是15和15，本次调查获取的样本数据的中位数是：15（元）；
故答案为：16元，10元，15元；
（4）估计该校本次活动捐款金额为10元的学生人数约为4500×32%＝1440（人）．
该校本次活动捐款金额为10元的学生人数为1440人．
【点睛】本题考查条形统计图、扇形统计图、用样本估计总体、中位数、众数，解题的关键是明确题意，找出所求问题需要的条件．
13．（1）捐款数被污染的数字为40，人数被污染的11；（2）该班捐款金额的众数是50元、中位数是40元
【分析】（1）根据全班的总人数，求得被污染的人数数字；再根据平均捐款求出被污染的捐款数字；
（2）根据中位数和众数的求解方法，即可求解．
【解析】解：（1）被污染出的人数数字为：50﹣3﹣6﹣11﹣13﹣6＝11，
设备污染的捐款数字为x，由题意可得，
，
解得x＝40，
答：捐款数被污染的数字为40，人数被污染的11；
（2）这50名学生捐款数出现次数最多的是50元，共有13人，因此捐款的众数是50元，
将这50名学生捐款数从小到大排列后，处在中间位置的两个数都是40元，因此捐款的中位数是40元，‘
答：该班捐款金额的众数是50元、中位数是40元．
【点睛】此题主要考查了统计量的计算，熟练掌握掌握各统计量的求解计算方法是解题的关键．
14．（1）85，80，85；（2）九（1）班
【分析】（1）根据条形统计图中的数据，可以得到、、的值；
（2）根据表格中的数据，可以得到哪个班级的复赛成绩较好，注意本题答案不唯一，只要合理即可．
【解析】解：（1），
九（2）的成绩按照从小到大排列是70，75，80，100，100，故，
，
故答案为：85，80，85；
（2）九（1）的成绩较好，理由：两个班的平均数一样，但是九（1）的中位数大于九（2）的中位数，说明九（1）的成绩高于九（2）．
【点睛】本题考查众数、中位数，解答本题的关键是明确题意，利用数形结合的思想解答．
15．(1)9
(2)；2
(3)3
【分析】（1）用总人数24减去已知人数即可；
（2）根据平均数和中位数的定义计算即可；
（3）根据中位数的定义可判断总人数不能超过27，从而得到最多补查的人数．
【解析】（1），
故答案为：9；
（2）第一次抽查中，人均读书，
中位数是2；
故答案为：；2
（3）∵1册和2册的人数和为14，中位数没有改变，
∴总人数不能超过27，
∴第二次最多抽查了3人．
故答案为：3．
【点睛】此题考查了平均数、中位数的计算，解题的关键是正确理解各概念的含义．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)