3.3方差和标准差 同步练习（含答案）

中小学教育资源及组卷应用平台
浙教版（2012）八年级数学下册 同步练习
3.3方 差 和 标 准 差
一、选择题
1．一组数据6，2，，5的极差为 （ ）
A．6 B．7 C．3 D．4
2．某校举行课间操比赛，甲、乙两个班各选出20名学生参加比赛，两个班参赛学生的平均身高都为，其方差分别为，则参赛学生身高比较整齐的班级是
（ ）
A．甲班 B．乙班 C．同样整齐 D．无法确定
3．甲乙两名同学进行了10次投掷铅球的测试，经计算，他们的平均成绩相同，若要比较这两名同学的成绩哪一位更稳定，通常还需要比较他们成绩的 （ ）
A．众数 B．中位数 C．方差 D．平均数
4．已知一组数据：3，4，5，6，5，7．那么这组数据的方差是 （ ）
A． B． C． D．
5．一组数据，，，，中，最后一个两位数的个位数字被墨迹覆盖，则这组数据不受影响的统计量是 （ ）
A．平均数 B．中位数 C．众数 D．极差
二、填空题
6．已知一组数据的方差为2，则这组数据的标准差为 _____．
7．如图，甲、乙两人比赛成绩的平均数相等，则______（填“”“”或“”）．
8．小明用计算一组数据的方差，那么 ____．
9．已知一组数据，，3，，6的中位数是1，则这组数据的标准差为_________．
10．已知一组数据，，，，的方差是，那么另一组数据，，，，的方差是____________．
三、解答题
11．八（1）班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表：
甲 7 8 9 7 10 10 9 10 10 10
乙 10 8 7 9 8 10 10 9 10 9
（1）甲队成绩的中位数是　　分，乙队成绩的众数是　　分；
（2）计算乙队的方差；
（3）已知甲队成绩的方差是1.4，则成绩较为整齐的是　　队．
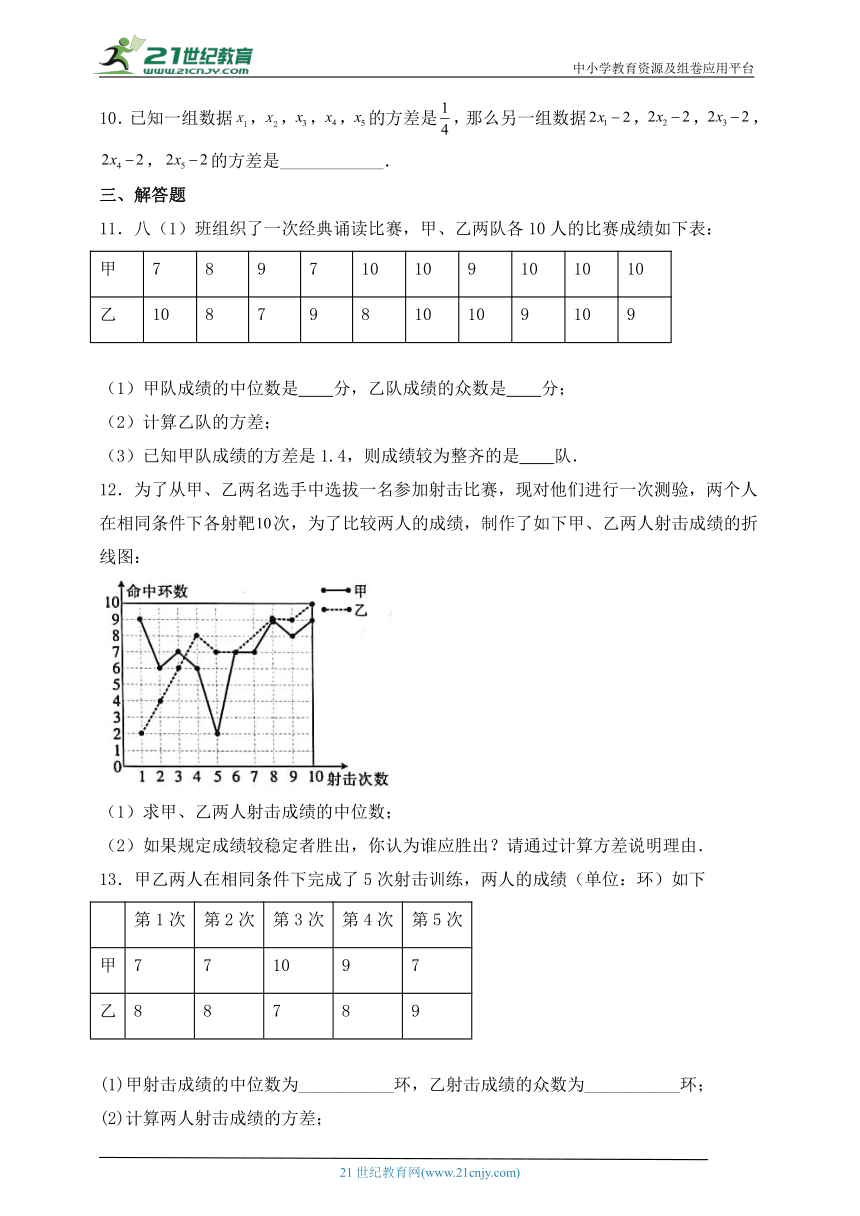
12．为了从甲、乙两名选手中选拔一名参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶次，为了比较两人的成绩，制作了如下甲、乙两人射击成绩的折线图：
（1）求甲、乙两人射击成绩的中位数；
（2）如果规定成绩较稳定者胜出，你认为谁应胜出？请通过计算方差说明理由．
13．甲乙两人在相同条件下完成了5次射击训练，两人的成绩（单位：环）如下
第1次 第2次 第3次 第4次 第5次
甲 7 7 10 9 7
乙 8 8 7 8 9
(1)甲射击成绩的中位数为___________环，乙射击成绩的众数为___________环；
(2)计算两人射击成绩的方差；
(3)根据训练成绩，你认为选派哪一名队员参赛更好，为什么？
14．某校为了解九年级各班男生引体向上情况，随机抽取九（1）班、九（3）班各5名同学进行测试，其有效次数分别为：九（1）班：，，，，；九（3）班：，，，，．现从平均数、众数、中位数、方差四个统计量对两个班的测试数据做如下分析：
平均数 众数 中位数 方差
九（1）班
九（3）班
根据以上信息，回答下列问题：
(1)请直接写出，，，的值．
(2)如果引体向上有效次数次的成绩为满分，不考虑其他因素，请以这名同学的成绩为样本，估计九年级名男生引体向上成绩达到满分的人数．
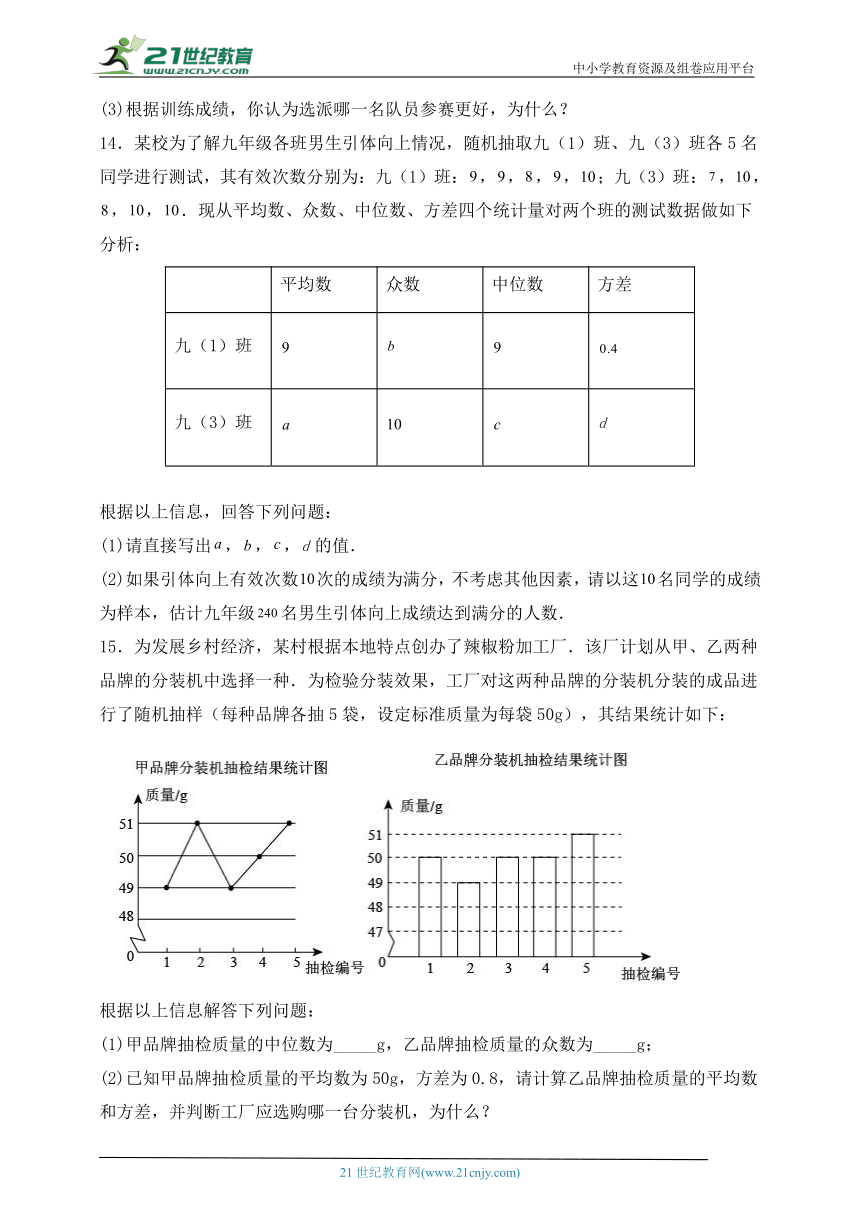
15．为发展乡村经济，某村根据本地特点创办了辣椒粉加工厂．该厂计划从甲、乙两种品牌的分装机中选择一种．为检验分装效果，工厂对这两种品牌的分装机分装的成品进行了随机抽样（每种品牌各抽5袋，设定标准质量为每袋50g），其结果统计如下：
根据以上信息解答下列问题：
(1)甲品牌抽检质量的中位数为_____g，乙品牌抽检质量的众数为_____g；
(2)已知甲品牌抽检质量的平均数为50g，方差为0.8，请计算乙品牌抽检质量的平均数和方差，并判断工厂应选购哪一台分装机，为什么？
参考答案：
1．B
【分析】根据极差的概念，求解即可，一组数据的最大值与最小值的差为极差．
【解析】根据极差的定义可得，这组数据的极差为，
故选：B．
【点睛】此题考查了极差的求解，解题的关键是掌握极差的定义．
2．B
【分析】根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
【解析】解：∵两个班参赛学生的平均身高都是，其方差分别是，
∴，
∴参赛学生身高比较整齐的班级是乙班．
故选：B．
【点睛】此题主要考查了方差，方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
3．C
【分析】根据方差的意义：是反映一组数据波动大小，稳定程度的量；方差越大，表明这组数据偏离平均数越大，即波动越大，反之也成立．
【解析】解：由于方差能反映数据的稳定性，需要比较这两名学生立定跳远成绩的方差．
故选：C．
【点睛】本题主要考查了方差的意义，解题的关键是掌握方差的意义：是反映一组数据波动大小，稳定程度的量；方差越大，表明这组数据偏离平均数越大，即波动越大，反之也成立．
4．A
【分析】先求出平均数，然后按照方差的计算公式计算方差即可．
【解析】解：这组数据的平均数为，
方差为
，
故选：A．
【点睛】本题考查了求一组数据的方差，掌握方差的计算公式是解题关键．
5．B
【分析】根据最后一个数字一定是个2位数，则从小到大的顺序不变，即中位数不变，据此即可求解．
【解析】解：依题意，最后一个数字一定是个2位数，则从小到大的顺序不变，即中位数不变，而平均数，众数，极差都要知道最后一个数，
故这组数据不受影响的统计量是中位数，
故选：B．
【点睛】本题考查了中位数，平均数，众数，极差，掌握以上知识是解题的关键．
6．
【分析】根据标准差是方差的算术平方根即可求解．
【解析】解：∵数据的方差是，
∴这组数据的标准差是；
故答案为：．
【点睛】此题考查了方差和标准差，熟练掌握两者之间的关系是解题的关键．
7．
【分析】根据方差的意义，结合折线统计图即可求解．
【解析】解：根据折线统计图得出甲波动较大，越不稳定，
则．
故答案为：
【点睛】本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．
8．30
【分析】根据方差公式可以确定这组数据的平均数和数据个数，相乘即可得出答案．
【解析】解：由，知这10个数据的平均数为3，
所以，
故答案为：30．
【点睛】本题考查了方差公式，解题关键是熟记方差计算公式，根据公式确定平均数与数据个数．
9．
【分析】先中位数的概念列出方程，求出的值，再根据方差的公式进行计算即可．
【解析】解：由题意知，数据，，3，，6的中位数是1，
，
这组数据的平均数为：，
这组数据的方差为：，
∴标准差为
故答案为：．
【点睛】本题考查了中位数和方差．将一组数据从小到大依次排列，把中间数据（或中间两数据的平均数）叫做中位数，关键是根据中位数的概念求得的值．
10．1
【分析】根据方差的变化规律可得：数据，，，，的方差是，再进行计算即可．
【解析】解：∵，，，，的方差是：，
∴另一组数据，，，，的方差是：，
∴另一组数据，，，，的方差是：，
故答案为：．
【点睛】本题考查了方差的知识，掌握当数据都加上一个数（或减去一个数）时，方差不变，即数据的波动情况不变；当数据都乘以一个数（或除以一个数）时，方差变为这个数的平方倍是解题的关键．
11．（1）9.5，10；（2）；（3）乙
【分析】（1）根据中位数的定义求出最中间两个数的平均数；根据众数的定义找出出现次数最多的数即可；
（2）先求出乙队的平均成绩，再根据方差公式进行计算；
（3）先比较出甲队和乙队的方差，再根据方差的意义即可得出答案．
【解析】（1）把甲队的成绩从小到大排列为：7，7，8，9，9，10，10，10，10，10，最中间两个数的平均数是（9＋10）÷2＝9.5（分），
则中位数是9.5分；
乙队成绩中10出现了4次，出现的次数最多，
则乙队成绩的众数是10分；
故答案为：9.5，10；
（2）乙队的平均成绩是：×（10×4＋8×2＋7＋9×3）＝9，
则方差是：×[4×（10 9）2＋2×（8 9）2＋（7 9）2＋3×（9 9）2]＝1；
（3）∵甲队成绩的方差是1.4，乙队成绩的方差是1，
∴成绩较为整齐的是乙队；
故答案为：乙．
【点睛】本题考查方差、中位数和众数，解题的关键是熟知其定义及计算方法．
12．（1）甲中位数为；乙中位数为；（2）甲胜出，理由见解析
【分析】（1）先把两名选手的成绩按从小到大排序，再求最中间两个数的平均数即可．
（2）利用方差公式，分别求出两名选手的方差，根据方差越小越稳定．
【解析】（1）由图可知，甲次射击成绩按从小到大排序为，，，，，，，，，，故中位数为；
乙次射击成绩按从小到大排序为，，，，，，，，，故中位数为．
（2）甲胜出．
理由：甲、乙两人射击成绩的平均数分别是
方差分别是
由可知，甲的射击成绩更稳定，即甲胜出．
【点睛】本题主要是考查了中位数与方差的知识，解题的关键要熟练中位数以及方差的求法．
13．(1)7，8
(2)甲的方差为，乙的方差为
(3)乙，理由见解析
【分析】（1）把甲的数据从小到大排列，确定中位数即可；根据乙数据中出现次数最多的数据确定众数即可；
（2）利用方差公式计算即可；
（3）根据平均数及方差确定乙队员参赛．
【解析】（1）解：把甲的数据从小到大排列，中间的数据是7，故中位数是7；
乙数据中出现次数最多的数据8，故众数是8；
故答案为：7，8．
（2）解：，
，
．
（3）解，选派乙队员参赛更好；
由于两个人的平均数相同，甲的方差大于乙的方差，乙的成绩更稳定，
所以选派乙队员参赛更好．
【点睛】本题考查了中位数、众数、方差等数据分析，解题关键是熟记公式，准确计算，利用相关数据做出判断．
14．(1)
(2)估计九年级名男生引体向上成绩达到满分的人数为人
【分析】（1）根据中位数、众数、平均数、方差的计算方法分别计算结果，得出答案．
（2）用总人数乘以样本中甲、乙班男生引体向上成绩达到满分的人数所占比例即可．
【解析】（1）九（1）班的测试数据中，的次数最多，因此甲的众数是，，九（3）班的平均数，将九（三）班的测试数据从小到大排列为，，，，，处在第位的数是，因此中位数是，即，九（3）班的方差，
所以，，，．
（2）（人）．
答：估计九年级名男生引体向上成绩达到满分的人数为人．
【点睛】本题考查了中位数、众数和平均数、方差的概念和计算方法，明确各个统计量的意义，反映数据的特征以及计算方法是正确解答的关键．
15．(1)50，50
(2)工厂应选购乙台分机，理由见解析
【分析】（1）根据中位数和众数的概念求解即可；
（2）根据统计图可得乙品牌5袋的质量，再根据平均数和方差的计算公式进行计算，最后与甲比较即可．
【解析】（1）∵甲品牌5袋质量从小到大排列为：49，49，50，51，51
∴甲品牌抽检质量的中位数为50g
∵乙品牌5袋中有3袋质量为50g，
∴乙品牌抽检质量的众数为50g
故答案为50，50
（2）工厂应选乙台分装机
∵乙品牌5袋质量分别为：50，49，50，50，51
∴乙品牌抽检质量的平均数为g
方差为
又∵甲品牌抽检质量的平均数为50g，方差为0.8
∴甲乙平均数相等，甲的方差>乙的方差
则工厂应选乙台分装机．
【点睛】】本题考查众数、中位数、平均数和方差计算方法，理解各个统计量的意义和记住平均数及方差公式是解决问题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)