浙教版八年级下册第三章数据分析 初步提升卷(含解析)
文档属性
| 名称 | 浙教版八年级下册第三章数据分析 初步提升卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 16:41:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
八年级下册第三章数据分析初步提升卷(含解析)
一、单选题(每题3分,共30分)
1.某中学举行歌咏比赛,六位评委对某位选手的打分如下(单位:分):77,82,78,91,83,75.去掉一个最高分和一个最低分后的平均分是( )
A.79分 B.80分 C.81分 D.82分
2.从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A. B.
C. D.
3.某校对学生一学期的各学科学业的总平均分是按如图所示的扇形图信息要求进行计算的已知该校八年级一班李明同学这个学期的数学成绩如表:
李明 平时作业 期中考试 期末考试
90 85 88
则李明这个学期数学的总平均分为( )
A.87.5 B.87.6 C.87.7 D.87.8
4.已知一组数据2,2,5,x,5,3有唯一的众数5,则x的值是( )
A.3 B.5 C.2 D.无法确定
5.八年级一班七个兴趣小组人数分别为4,4,5,x,6,6,7,已知这组数据的平均数是5,则这组数据的中位数是( )
A.7 B.6 C.5 D.4
6.下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣7,﹣5,7的中位数和平均数都是0
7.若x1,x2,x3, ,xn的平均数为8,方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
8.在一场“中华诗词大赛”中,有23名选手进行比赛,其中成绩排名前12的选手将进入复赛,每名选手都只知道自己的得分(注:每名选手的得分都不相同),要知道自己是否进入复赛,还应知道所有选手成绩的( )
A.平均数 B.众数 C.中位数 D.方差
9.为了从四名同学中选出一人参加计算机编程比赛,对他们进行了多次测试,并对每个人的测试成绩的平均数及方差进行了统计(如下表),则应选的同学是( )
学生 学生一 学生二 学生三 学生四
平均数 95 96 96 95
方差 5 5 4.8 4.8
A.学生一 B.学生二 C.学生三 D.学生四
10.以2022年北京冬奥会为契机,某学校开展以“弘扬奥林匹克精神,感受冰雪运动魅力”为主题的冰雪嘉年华实践课程.为了解学生掌握滑雪技巧及滑雪水平等情况,教练分别对甲、乙两名学生10次训练的结果进行了统计,其中每次训练的成绩分别为5分,4分,3分,2分,1分五档.统计结果如图所示,下列结论正确的是( )
A., B.,
C., D.,
11.一组数据:的平均数为,众数为,中位数为,则以下判断正确的是( )
A.一定出现在中
B.一定出现在中
C.一定出现在中
D.,,都不会出现在中
二、填空题(每空2分,共20分)
12.某生产小组6名工人某天加工零件的个数分别是10,10,11,12,8,10,则这组数据的众数为 .
13.已知五个正数 , , , , ,平均数是4,方差为2,则 , , , , 这五个数的平均数是 ,方差是 .
14.某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的中位数是 .
15.为迎接体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一的众数是13,平均数是12,那么这组数据的方差是 。
16.某学校九(1)班40名同学的期中测试成绩分别为 , , ,……, .已知 + + +……+ = 4800,y= + + +……+ ,当y取最小值时, 的值为 .
三、解答题
17.已知5个数a1,a2,a3,a4,a5的平均数为m,则
(1)a1,a2,a3,0,a4,a5,这6个数的平均数为 ;
(2)2a1,2a2,2a3,2a4,2a5这5个数的平均数为 ;
(3)若5个数b1,b2,b3,b4,b5的平均数为n,则2a1+b1,2a2+b2,2a3+b3,2a4+b4,2a5+b5这5个数的平均数为 。
18.某养鱼个体经营户在鱼塘放养了5500条草鱼苗,鱼苗的成活率为90%.养殖一段时间后,想估计鱼塘中产量,随机网了三次,第一次网出30条鱼,平均每条鱼的重量是1kg;第二次网出了45条鱼,平均每条鱼的重量是1.3kg;第三次网出了35条鱼,平均每条鱼的重量是1.2kg,请你估计鱼塘中鱼的总重量是多少kg?
19.某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为 ,图①中m的值为 ;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
20.某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级各有150人参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下:
七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分段整理样本数据并补全表格:
分析数据:补全下列表格中的统计量:
得出结论:你认为抽取的学生哪个年级的成绩较为稳定?并说明理由.
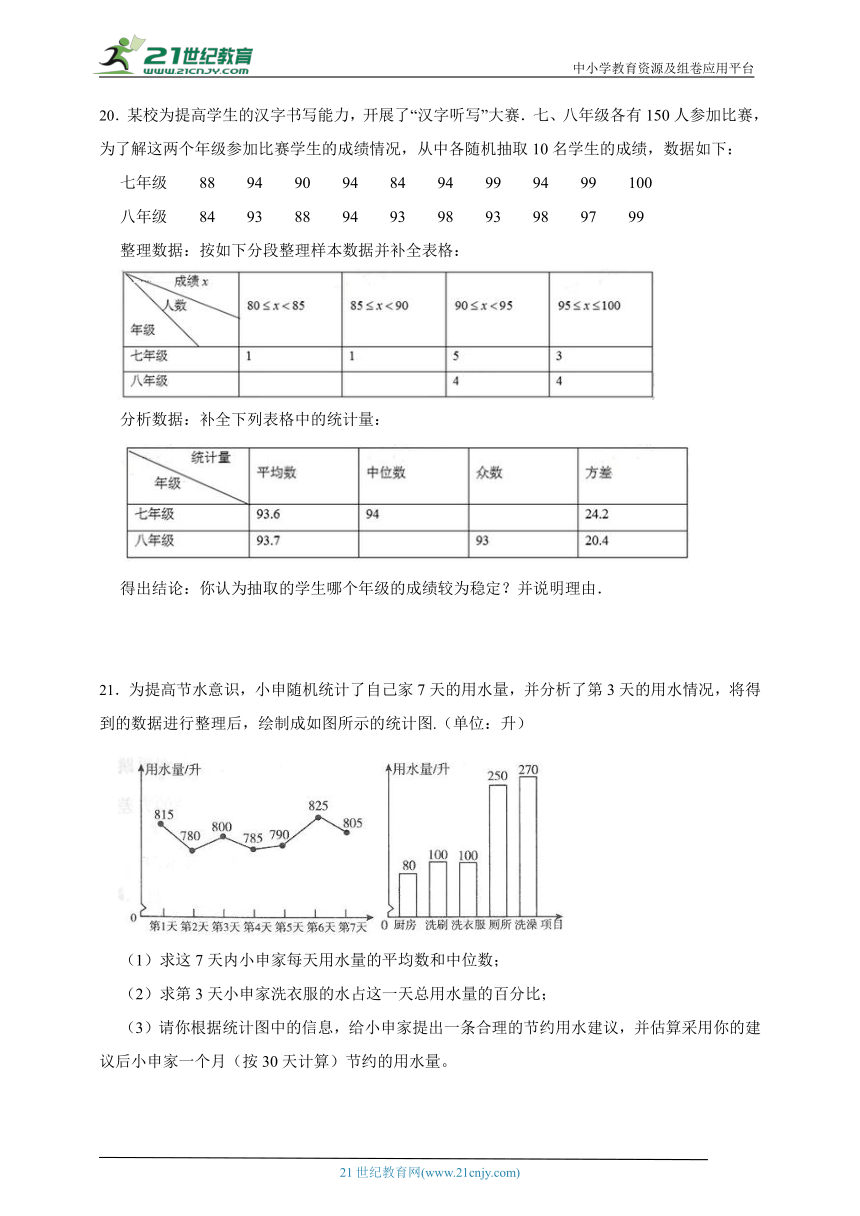
21.为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)节约的用水量。
22.电影《长津湖》和《水门桥》是两部聚焦抗美援朝历史的影片,从观看过这两部电影的学生中各随机抽取了20名学生进行调查,让他们给这两部电影评分,下列图表是调查中的部分信息.
根据以上信息,解答下列问题:
(1)电影《长津湖》得分的中位数和众数分别是多少?
(2)电影《水门桥》得分的平均数是多少?
(3)若该校有200名学生观看过这两部影片,且他们都对这两部作品进行评分,你认为这两部作品一共可以得到多少个满分?
23.已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.现在有行驶路程S(千米)与行驶时间t(时)的函数图象(如图①)、上周货运量折线统计图(如图②)、货运收费项目及收费标准表等信息如下:
货运收费项目及收费标准表
运输工具 运输费单价:元/(吨·千米) 冷藏费单价:元/(吨 时) 固定费用:元/次
汽车 2 5 200
火车 1.6 5 2280
(1)请你根据以上信息,分别求出汽车和火车的速度;
(2)设每天用汽车和火车运输的总费用分别为(元)和(元),分别求、与x的函数关系式(不必写出x的取值范围)及x为何值时;(总费用=运输费十冷藏费十固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前下周预定哪种运输工具,才能使每天的运输总费用较省?
24.《生物多样性公约》第十五次缔约方大会(COP15)重新确定于2021年5月17日至30日在云南省昆明市举办.“生物多样性”的目标、方法和全球通力合作,将成为国际范围的热点关注内容.为广泛宣传云南生物多样性,某校组织七、八年级各200名学生对《云南的生物多样性》白皮书相关知识进行学习并组织定时测试.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的竞赛成绩,相关数据统计、整理如下:
【收集数据】
七年级10名同学测试成绩统计如下:
72,84,72,91,79,69,78,85,75,95
八年级10名同学测试成绩统计如下:
85,72,92,84,80,74,75,80,76,82
【整理数据】两组数据各分数段,如下表所示:
成绩
七年级 1 5 2 a
八年级 0 4 5 1
【分析数据】两组数据的平均数、中位数、众数、方差如下表:
年级统计量 平均数 中位数 众数 方差
七年级 80 b 72 66.6
八年级 80 80 c
【问题解决】根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)计算八年级同学测试成绩的方差是:.请估计哪个年级的竞赛成绩更整齐?
(3)按照比赛规定90分及其以上算优秀,请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人?
(4)根据以上数据,你认为该校七、八年级中哪个年级学生知识竞赛成绩更好?请说明理由(至少写出两条理由).
答案解析部分
1.【答案】B
【解析】【解答】解∵去掉一个最高分和一个最低分,
∴剩下数据的平均数==80(分),
故答案为:B.
【分析】根据题意,去掉一个最高和最低分后还剩下4个数据,代入公式求得4个成绩的平均值即可.
2.【答案】B
【解析】【解答】解:由题意知,a个x1的和为ax1,b个x2的和为bx2,c个x3的和为cx3,数据总共有a+b+c个,所以这个样本的平均数=,
故答案为:B.
【分析】利用平均数的计算方法求解即可。
3.【答案】A
【解析】【解答】解:依据题意得这学期数学总平均成绩就是李明平时、期中、期末数学成绩的加权平均数
∴这学期数学总平均成绩
故答案为:A.
【分析】利用平时的成绩×所占的比例+期中成绩×所占的比例+期末成绩×所占的比例可得平均成绩.
4.【答案】B
【解析】【解答】解:根据题意,此题中有唯一的众数5,所以x=5.
故答案为:B.
【分析】利用众数的定义求解即可。
5.【答案】C
【解析】【解答】解:∵这组数据的平均数是5,
∴=5,
∴x=3,
∴这组数据按从小到大排列为3,4,4,5,6,6,7,
∴中位数为5.
故答案为:C.
【分析】根据平均数的公式列出方程,求出x的值,再根据中位数的定义即可得出答案.
6.【答案】D
【解析】【解答】解:A、数据3,4,4,7,3的众数是3和4,A选项不符合题意;
B、数据0,1,2,5,a中,因为a的大小无法确定,所以中位数也无法确定,B不符合题意;
C、例如2,3,3,4这组数据的中位数和众数均为3,C选项不符合题意;
D、数据0,5,-7,-5,7按从小到大排列为-7,-5,0,5,7,中位数和平均数均为0,D符合题意.
故答案为:D.
【分析】众数为一组数据中出现次数最多的数,可以一个或多个或没有;中位数为数据按大小顺序排列后,最中间的数字(数据个数为偶数时,是最中间两数的平均数);平均数根据所有数据之后除以数据个数即可求出. 据此判断即可得到正确答案.
7.【答案】C
【解析】【解答】解:样本x1+2,x2+2,x3+2,…xn+2,对于样本x1,x2,x3,…xn来说,
每个数据均在原来的基础上增加了2,根据平均数、方差的变化规律得:
平均数较前增加2,而方差不变,即:平均数为8+2=10,方差为2,
故答案为:C.
【分析】先求出平均数较前增加2,而方差不变,再求解即可。
8.【答案】C
【解析】【解答】解:根据题意,选手在得知自己的成绩后,想要判断自己能否进入前12名,只需将自己的成绩与第12名的成绩比较即可,
由中位数的意义,将23人的成绩从大到小排列,而23位选手的得分互不相同,则中位数即第12名的成绩,
故只需知道所有选手成绩的中位数即可.
故答案为:C.
【分析】将23人的成绩从大到小进行排列,中位数即第12名的成绩,据此判断.
9.【答案】C
【解析】【解答】解:根据题意得:学生二与学生三成绩的平均数高于学生一与学生四的,且学生三成绩的方差低于学生二的,
∴应选的同学是学生三.
故答案为:C
【分析】利用平均数和方差的计算方法及性质求解即可。
10.【答案】A
【解析】【解答】解:由题意,(分),
,
∴,
由图知,甲的波动大,∴,
故答案为:A.
【分析】根据折线统计图中的数据,先分别求出甲、乙的平均数,再根据数据的波动越大,方差越大即可解答.
11.【答案】B
【解析】【解答】解:A、如数据0,1,1,4这四个数的平均数是1.5,不是这组数中的某个数,不符合题意;
B、众数是一组数据中出现次数最多的数,它一定是数据中的数,符合题意;
C、如数据1,2,3,4的中位数是2.5,不是这组数中的某个数,不符合题意;
D、众数是一组数据中出现次数最多的数,它一定是数据中的数,不符合题意.
故答案为:B.
【分析】利用平均数、众数和中位数的定义及计算方法求解即可。
12.【答案】10
【解析】【解答】解:在数据10,10,11,12,8,10中,因为10出现的次数最多,出现了3次,所以10为这组数据的众数.
故答案为:10.
【分析】在这组数据中出现次数最多的数据叫作这组数据的众数,据此解答.
13.【答案】13;18
【解析】【解答】解: 个正数 , , , , ,平均数是4,方差为2,
, ,
, , , , 这五个数的平均数是 ,
, , , , 这五个数的方差为 ,
故答案为:13,18.
【分析】由题意可得a+b+c+d+e=20,,利用平均数及方程的公式求出3a+1, , , , 这五个数的平均数和方差即可.
14.【答案】7.5
【解析】【解答】解:因图中是按从小到大的顺序排列的,最中间的环数是7环、8环,则中位数是 =7.5(环).
故答案为:7.5.
【分析】根据中位数的定义先把数据从小到大的顺序排列,找出最中间的数或最中间两个位置的数的平均数即可得出答案.
15.【答案】
【解析】【解答】解:∵平均数为12,
∴这组数据的和=12×7=84,
所以被墨汁覆盖的数的和=84-11-12-13-12=36,
又∵这组数据的众数为13,
∴被覆盖的三个数为:10,13,13,
所以这组数据的方差s2=
=.
故答案为:.
【分析】根据已知条件可推出被墨汁覆盖的三个数是10,13,13,再根据方差公式进行计算即可.
16.【答案】120
【解析】【解答】解:y=40a
2-2(a
1+a
2+a
3+…+a
40)a+a
12+a
22+a
3)
2+…+a
402,
因为40>0,
所以当a=
时,y有最小值.
【分析】 利用完全平方公式得到y=40a2-2(a1+a2+a3+…+a40)a+a12+a22+a3)2+…+a402,则可把y看作a的二次函数,然后根据二次函数的性质求解.
17.【答案】(1)
(2)2m
(3)2m+n
【解析】【解答】解:(1)∵a1,a2,a3,a4,a5的平均数是m,
∴a1+a2+a3+a4+a5=5m,
∴a1+a2+a3+0+a4+a5=5m
∴a1,a2,a3,0,a4,a5的平均数为: ;
(2)∵a1+a2+a3+a4+a5=5m,
∴2a1,2a2,2a3,2a4,2a5这5个数的平均数为:2(a1+a2+a3+a4+a5)÷5=10m÷5=2m,
(3)∵b1,b2,b3,b4,b5的平均数是n,
∴b1+b2+b3+b4+b5=5n,
又∵2(a1+a2+a3+a4+a5)=10m,
∴2a1+b1,2a2+b2,2a3+b3,2a4+b4,2a5+b5 的平均数为,
(10m+5n)÷5=2m+n,
故答案为:2m+n.
【分析】(1)利用平均数计算公式,代入数据及平均数先求出a1,a2,a3,a4,a5的和,再利用公式求出a1,a2,a3,0,a4,a5六个数平均数即可;
(2)由(1)可知a1,a2,a3,a4,a5的和,可求出 2a1,2a2,2a3,2a4,2a5这5个数的和,利用平均数计算公式即可求出这五个数的平均数;
(3)先求出b1,b2,b3,b4,b5五个数的和,又由(2)知2a1,2a2,2a3,2a4,2a5这五个数的和,再先加求总和除以5即可求出2a1+b1,2a2+b2,2a3+b3,2a4+b4,2a5+b5这五个数的平均数.
18.【答案】解:由题意得: kg.
答:估计鱼塘中鱼的总重量是5872.5kg.
【解析】【分析】先求出样本平均数,然后乘以5500,再乘以90%即得结论.
19.【答案】解:(Ⅰ)50,20;
(Ⅱ)平均数:吨,
∵用水量6吨的家庭个数为16,最多,
∴众数=6吨,
∵一共50个数据,最中间的数据为第25和第26个数据,
∴中位数=(6+6)÷2=6吨.
答: 这组月均用水量数据的平均数为5.9吨,众数为6吨,中位数为6吨.
【解析】【解答】解:(Ⅰ)本次调查的家庭个数=8+12+16+10+4=50个,
m%=10÷50×100%=20%.
故答案为:50,20;
【分析】(Ⅰ)由条形图可知各个用水量的家庭个数,把所有家庭个数相加可求得本次调查的家庭个数,再用用水量为6.5吨的家庭个数除以总家庭个数,即可求出m的值;
(Ⅱ)利用加权平均数的计算公式,将数据代入公式计算即可求的组月均用水量数据的平均数,由条形统计图可知用水量6吨的家庭个数是16为最多,可求得众数,再由50个数据,最中间的数据为第25和第26个数据,将这两个数据求和再除以2,即可求出中位数.
20.【答案】解:整理数据:按如下分段整理样本数据并补全表格:
分析数据:补全下列表格中的统计量:
八年级的成绩较为稳定,理由:∵七年级的方差=24.2,八年级的方差=20.4,24.2>20.4,∴八年级的成绩较为稳定.
故答案为:1,1,93.5,94.
【解析】【分析】根据中位数,众数和方差的定义即可得到结论.
21.【答案】(1)解:这7天内小申家每天用水量的平均数为==800(升)
将这7天的用水量从小到大重新排列为:780,785,790,800,805,815,825,∴用水量的中位数为800升。
(2)解:×100%=12.5%,答:第3天小申家洗衣服的水占这一天总用水量的百分比为12.5%。
(3)解:答案不唯一,例如:小申家冲厕所的用水量较大,可以用洗衣服的水冲厕所。采用以上建议,每天可节约用水100升,一个月估计可以节约用水100×30=3000(升)。
【解析】【分析】(1)根据平均数和中位数的定义进行计算即可求得;
(2)用洗衣服的水量除以第三天的用水总量即可求得;
(3)根据条形图给出节水的合理性建议均可,例如将洗衣服后的水用为冲厕所等.
22.【答案】(1)解:∵一共抽查了20个人,∴中位数等于第十个和第十一个学生评分的平均数;由图可知,第十个人评分8分,第十一个人平分9分;∴中位数=;由图可知,评分为9分的人数最多;∴众数是9
(2)解:评分为10分的人数所占百分比=1-10%-20%-15%-20%=35%=0.35∴平均数=,答:电影《水门桥》得分的平均数是8.5;
(3)解:抽出的20人中,《长津湖》得到满分的有4个,《水门桥》得到满分的有(个),所以(个).答:这两部作品一共可以得到110个满分.
【解析】【分析】(1)利用中位数和众数的定义及计算方法求解即可;
(2)利用平均数的计算方法求解即可;
(3)分别求出《长津湖》和《水门桥》的人数,再相加即可。
23.【答案】(1)解:根据图表上点的坐标为:(2,120),(2,200),
∴汽车的速度为 60千米/时,火车的速度为 100千米/时.
(2)解:依据题意得出:
y汽=240×2x+×5x+200=500x+200;
y火=240×1.6x+×5x+2280=396x+2280.
若y 汽>y 火,得出500x+200>396x+2280.
∴x>20;
(3)解:上周货运量=(17+20+19+22+22+23+24)÷7=21>20,
从平均数分析,建议预定火车费用较省.
从折线图走势分析,上周货运量周四(含周四)后大于20且呈上升趋势,
建议预订火车费用较省.
【解析】【分析】(1)根据图象可得火车2小时行驶的路程为200千米,汽车2小时行驶的路程为120千米,然后根据路程÷时间=速度进行求解;
(2)根据AB两地的距离×汽车的运费+AB两地的距离÷汽车的速度×冷藏价格+固定费用可得y汽与x的关系式;根据AB两地的距离×汽车的运费+AB两地的距离÷火车的速度×冷藏价格+固定费用可得y火与x的关系式,然后令y汽>y火,求出x的范围即可;
(3)根据平均数的计算方法求出上周货运的平均数,然后根据平均数的大小以及折线统计图的趋势进行分析判断.
24.【答案】(1)2;78.5;80
(2)解:∵七年级同学测试成绩的方差是66.6, 八年级同学测试成绩的方差是33,
∴,
∴估计八年级学生的竞赛成绩更整齐些.
(3)解:由题意得(人),
∴这两个年级竞赛成绩达到优秀学生的人数共约60人.
(4)解:可以推断出八年级学生的数学水平较高,
理由为两班平均数相同,八年级的中位数高于七年级;八年级的众数高于七年级,
说明八年级学生的竞赛成绩更好(答案不唯一).
【解析】【解答】(1)解:将七年级抽样成绩重新排列为:69,72,72,75,78,79,84,85,91,95,其中在90≤x<100范围内的数据有2个,
故a=2.
中位为b=(分),
将八年级的成绩出现次数最多是80分,共出现2次,
∴众数c=80(分),
故答案为:2,78.5,80;
【分析】(1)根据题干中的数据求出a的值,再利用众数和中位数的定义求出b、c的值即可;
(2)利用方差的定义及计算方法求解即可;
(3)先求出两个班“优秀”的人数,再相加即可;
(4)根据平均数和中位数的性质求解即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
八年级下册第三章数据分析初步提升卷(含解析)
一、单选题(每题3分,共30分)
1.某中学举行歌咏比赛,六位评委对某位选手的打分如下(单位:分):77,82,78,91,83,75.去掉一个最高分和一个最低分后的平均分是( )
A.79分 B.80分 C.81分 D.82分
2.从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A. B.
C. D.
3.某校对学生一学期的各学科学业的总平均分是按如图所示的扇形图信息要求进行计算的已知该校八年级一班李明同学这个学期的数学成绩如表:
李明 平时作业 期中考试 期末考试
90 85 88
则李明这个学期数学的总平均分为( )
A.87.5 B.87.6 C.87.7 D.87.8
4.已知一组数据2,2,5,x,5,3有唯一的众数5,则x的值是( )
A.3 B.5 C.2 D.无法确定
5.八年级一班七个兴趣小组人数分别为4,4,5,x,6,6,7,已知这组数据的平均数是5,则这组数据的中位数是( )
A.7 B.6 C.5 D.4
6.下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,﹣7,﹣5,7的中位数和平均数都是0
7.若x1,x2,x3, ,xn的平均数为8,方差为2,则关于x1+2,x2+2,x3+2,……,xn+2,下列结论正确的是( )
A.平均数为8,方差为2 B.平均数为8,方差为4
C.平均数为10,方差为2 D.平均数为10,方差为4
8.在一场“中华诗词大赛”中,有23名选手进行比赛,其中成绩排名前12的选手将进入复赛,每名选手都只知道自己的得分(注:每名选手的得分都不相同),要知道自己是否进入复赛,还应知道所有选手成绩的( )
A.平均数 B.众数 C.中位数 D.方差
9.为了从四名同学中选出一人参加计算机编程比赛,对他们进行了多次测试,并对每个人的测试成绩的平均数及方差进行了统计(如下表),则应选的同学是( )
学生 学生一 学生二 学生三 学生四
平均数 95 96 96 95
方差 5 5 4.8 4.8
A.学生一 B.学生二 C.学生三 D.学生四
10.以2022年北京冬奥会为契机,某学校开展以“弘扬奥林匹克精神,感受冰雪运动魅力”为主题的冰雪嘉年华实践课程.为了解学生掌握滑雪技巧及滑雪水平等情况,教练分别对甲、乙两名学生10次训练的结果进行了统计,其中每次训练的成绩分别为5分,4分,3分,2分,1分五档.统计结果如图所示,下列结论正确的是( )
A., B.,
C., D.,
11.一组数据:的平均数为,众数为,中位数为,则以下判断正确的是( )
A.一定出现在中
B.一定出现在中
C.一定出现在中
D.,,都不会出现在中
二、填空题(每空2分,共20分)
12.某生产小组6名工人某天加工零件的个数分别是10,10,11,12,8,10,则这组数据的众数为 .
13.已知五个正数 , , , , ,平均数是4,方差为2,则 , , , , 这五个数的平均数是 ,方差是 .
14.某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的中位数是 .
15.为迎接体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一的众数是13,平均数是12,那么这组数据的方差是 。
16.某学校九(1)班40名同学的期中测试成绩分别为 , , ,……, .已知 + + +……+ = 4800,y= + + +……+ ,当y取最小值时, 的值为 .
三、解答题
17.已知5个数a1,a2,a3,a4,a5的平均数为m,则
(1)a1,a2,a3,0,a4,a5,这6个数的平均数为 ;
(2)2a1,2a2,2a3,2a4,2a5这5个数的平均数为 ;
(3)若5个数b1,b2,b3,b4,b5的平均数为n,则2a1+b1,2a2+b2,2a3+b3,2a4+b4,2a5+b5这5个数的平均数为 。
18.某养鱼个体经营户在鱼塘放养了5500条草鱼苗,鱼苗的成活率为90%.养殖一段时间后,想估计鱼塘中产量,随机网了三次,第一次网出30条鱼,平均每条鱼的重量是1kg;第二次网出了45条鱼,平均每条鱼的重量是1.3kg;第三次网出了35条鱼,平均每条鱼的重量是1.2kg,请你估计鱼塘中鱼的总重量是多少kg?
19.某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为 ,图①中m的值为 ;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
20.某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级各有150人参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下:
七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分段整理样本数据并补全表格:
分析数据:补全下列表格中的统计量:
得出结论:你认为抽取的学生哪个年级的成绩较为稳定?并说明理由.
21.为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条合理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)节约的用水量。
22.电影《长津湖》和《水门桥》是两部聚焦抗美援朝历史的影片,从观看过这两部电影的学生中各随机抽取了20名学生进行调查,让他们给这两部电影评分,下列图表是调查中的部分信息.
根据以上信息,解答下列问题:
(1)电影《长津湖》得分的中位数和众数分别是多少?
(2)电影《水门桥》得分的平均数是多少?
(3)若该校有200名学生观看过这两部影片,且他们都对这两部作品进行评分,你认为这两部作品一共可以得到多少个满分?
23.已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.现在有行驶路程S(千米)与行驶时间t(时)的函数图象(如图①)、上周货运量折线统计图(如图②)、货运收费项目及收费标准表等信息如下:
货运收费项目及收费标准表
运输工具 运输费单价:元/(吨·千米) 冷藏费单价:元/(吨 时) 固定费用:元/次
汽车 2 5 200
火车 1.6 5 2280
(1)请你根据以上信息,分别求出汽车和火车的速度;
(2)设每天用汽车和火车运输的总费用分别为(元)和(元),分别求、与x的函数关系式(不必写出x的取值范围)及x为何值时;(总费用=运输费十冷藏费十固定费用)
(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前下周预定哪种运输工具,才能使每天的运输总费用较省?
24.《生物多样性公约》第十五次缔约方大会(COP15)重新确定于2021年5月17日至30日在云南省昆明市举办.“生物多样性”的目标、方法和全球通力合作,将成为国际范围的热点关注内容.为广泛宣传云南生物多样性,某校组织七、八年级各200名学生对《云南的生物多样性》白皮书相关知识进行学习并组织定时测试.现分别在七、八两个年级中各随机抽取了10名学生,统计这部分学生的竞赛成绩,相关数据统计、整理如下:
【收集数据】
七年级10名同学测试成绩统计如下:
72,84,72,91,79,69,78,85,75,95
八年级10名同学测试成绩统计如下:
85,72,92,84,80,74,75,80,76,82
【整理数据】两组数据各分数段,如下表所示:
成绩
七年级 1 5 2 a
八年级 0 4 5 1
【分析数据】两组数据的平均数、中位数、众数、方差如下表:
年级统计量 平均数 中位数 众数 方差
七年级 80 b 72 66.6
八年级 80 80 c
【问题解决】根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)计算八年级同学测试成绩的方差是:.请估计哪个年级的竞赛成绩更整齐?
(3)按照比赛规定90分及其以上算优秀,请估计这两个年级竞赛成绩达到优秀学生的人数共有多少人?
(4)根据以上数据,你认为该校七、八年级中哪个年级学生知识竞赛成绩更好?请说明理由(至少写出两条理由).
答案解析部分
1.【答案】B
【解析】【解答】解∵去掉一个最高分和一个最低分,
∴剩下数据的平均数==80(分),
故答案为:B.
【分析】根据题意,去掉一个最高和最低分后还剩下4个数据,代入公式求得4个成绩的平均值即可.
2.【答案】B
【解析】【解答】解:由题意知,a个x1的和为ax1,b个x2的和为bx2,c个x3的和为cx3,数据总共有a+b+c个,所以这个样本的平均数=,
故答案为:B.
【分析】利用平均数的计算方法求解即可。
3.【答案】A
【解析】【解答】解:依据题意得这学期数学总平均成绩就是李明平时、期中、期末数学成绩的加权平均数
∴这学期数学总平均成绩
故答案为:A.
【分析】利用平时的成绩×所占的比例+期中成绩×所占的比例+期末成绩×所占的比例可得平均成绩.
4.【答案】B
【解析】【解答】解:根据题意,此题中有唯一的众数5,所以x=5.
故答案为:B.
【分析】利用众数的定义求解即可。
5.【答案】C
【解析】【解答】解:∵这组数据的平均数是5,
∴=5,
∴x=3,
∴这组数据按从小到大排列为3,4,4,5,6,6,7,
∴中位数为5.
故答案为:C.
【分析】根据平均数的公式列出方程,求出x的值,再根据中位数的定义即可得出答案.
6.【答案】D
【解析】【解答】解:A、数据3,4,4,7,3的众数是3和4,A选项不符合题意;
B、数据0,1,2,5,a中,因为a的大小无法确定,所以中位数也无法确定,B不符合题意;
C、例如2,3,3,4这组数据的中位数和众数均为3,C选项不符合题意;
D、数据0,5,-7,-5,7按从小到大排列为-7,-5,0,5,7,中位数和平均数均为0,D符合题意.
故答案为:D.
【分析】众数为一组数据中出现次数最多的数,可以一个或多个或没有;中位数为数据按大小顺序排列后,最中间的数字(数据个数为偶数时,是最中间两数的平均数);平均数根据所有数据之后除以数据个数即可求出. 据此判断即可得到正确答案.
7.【答案】C
【解析】【解答】解:样本x1+2,x2+2,x3+2,…xn+2,对于样本x1,x2,x3,…xn来说,
每个数据均在原来的基础上增加了2,根据平均数、方差的变化规律得:
平均数较前增加2,而方差不变,即:平均数为8+2=10,方差为2,
故答案为:C.
【分析】先求出平均数较前增加2,而方差不变,再求解即可。
8.【答案】C
【解析】【解答】解:根据题意,选手在得知自己的成绩后,想要判断自己能否进入前12名,只需将自己的成绩与第12名的成绩比较即可,
由中位数的意义,将23人的成绩从大到小排列,而23位选手的得分互不相同,则中位数即第12名的成绩,
故只需知道所有选手成绩的中位数即可.
故答案为:C.
【分析】将23人的成绩从大到小进行排列,中位数即第12名的成绩,据此判断.
9.【答案】C
【解析】【解答】解:根据题意得:学生二与学生三成绩的平均数高于学生一与学生四的,且学生三成绩的方差低于学生二的,
∴应选的同学是学生三.
故答案为:C
【分析】利用平均数和方差的计算方法及性质求解即可。
10.【答案】A
【解析】【解答】解:由题意,(分),
,
∴,
由图知,甲的波动大,∴,
故答案为:A.
【分析】根据折线统计图中的数据,先分别求出甲、乙的平均数,再根据数据的波动越大,方差越大即可解答.
11.【答案】B
【解析】【解答】解:A、如数据0,1,1,4这四个数的平均数是1.5,不是这组数中的某个数,不符合题意;
B、众数是一组数据中出现次数最多的数,它一定是数据中的数,符合题意;
C、如数据1,2,3,4的中位数是2.5,不是这组数中的某个数,不符合题意;
D、众数是一组数据中出现次数最多的数,它一定是数据中的数,不符合题意.
故答案为:B.
【分析】利用平均数、众数和中位数的定义及计算方法求解即可。
12.【答案】10
【解析】【解答】解:在数据10,10,11,12,8,10中,因为10出现的次数最多,出现了3次,所以10为这组数据的众数.
故答案为:10.
【分析】在这组数据中出现次数最多的数据叫作这组数据的众数,据此解答.
13.【答案】13;18
【解析】【解答】解: 个正数 , , , , ,平均数是4,方差为2,
, ,
, , , , 这五个数的平均数是 ,
, , , , 这五个数的方差为 ,
故答案为:13,18.
【分析】由题意可得a+b+c+d+e=20,,利用平均数及方程的公式求出3a+1, , , , 这五个数的平均数和方差即可.
14.【答案】7.5
【解析】【解答】解:因图中是按从小到大的顺序排列的,最中间的环数是7环、8环,则中位数是 =7.5(环).
故答案为:7.5.
【分析】根据中位数的定义先把数据从小到大的顺序排列,找出最中间的数或最中间两个位置的数的平均数即可得出答案.
15.【答案】
【解析】【解答】解:∵平均数为12,
∴这组数据的和=12×7=84,
所以被墨汁覆盖的数的和=84-11-12-13-12=36,
又∵这组数据的众数为13,
∴被覆盖的三个数为:10,13,13,
所以这组数据的方差s2=
=.
故答案为:.
【分析】根据已知条件可推出被墨汁覆盖的三个数是10,13,13,再根据方差公式进行计算即可.
16.【答案】120
【解析】【解答】解:y=40a
2-2(a
1+a
2+a
3+…+a
40)a+a
12+a
22+a
3)
2+…+a
402,
因为40>0,
所以当a=
时,y有最小值.
【分析】 利用完全平方公式得到y=40a2-2(a1+a2+a3+…+a40)a+a12+a22+a3)2+…+a402,则可把y看作a的二次函数,然后根据二次函数的性质求解.
17.【答案】(1)
(2)2m
(3)2m+n
【解析】【解答】解:(1)∵a1,a2,a3,a4,a5的平均数是m,
∴a1+a2+a3+a4+a5=5m,
∴a1+a2+a3+0+a4+a5=5m
∴a1,a2,a3,0,a4,a5的平均数为: ;
(2)∵a1+a2+a3+a4+a5=5m,
∴2a1,2a2,2a3,2a4,2a5这5个数的平均数为:2(a1+a2+a3+a4+a5)÷5=10m÷5=2m,
(3)∵b1,b2,b3,b4,b5的平均数是n,
∴b1+b2+b3+b4+b5=5n,
又∵2(a1+a2+a3+a4+a5)=10m,
∴2a1+b1,2a2+b2,2a3+b3,2a4+b4,2a5+b5 的平均数为,
(10m+5n)÷5=2m+n,
故答案为:2m+n.
【分析】(1)利用平均数计算公式,代入数据及平均数先求出a1,a2,a3,a4,a5的和,再利用公式求出a1,a2,a3,0,a4,a5六个数平均数即可;
(2)由(1)可知a1,a2,a3,a4,a5的和,可求出 2a1,2a2,2a3,2a4,2a5这5个数的和,利用平均数计算公式即可求出这五个数的平均数;
(3)先求出b1,b2,b3,b4,b5五个数的和,又由(2)知2a1,2a2,2a3,2a4,2a5这五个数的和,再先加求总和除以5即可求出2a1+b1,2a2+b2,2a3+b3,2a4+b4,2a5+b5这五个数的平均数.
18.【答案】解:由题意得: kg.
答:估计鱼塘中鱼的总重量是5872.5kg.
【解析】【分析】先求出样本平均数,然后乘以5500,再乘以90%即得结论.
19.【答案】解:(Ⅰ)50,20;
(Ⅱ)平均数:吨,
∵用水量6吨的家庭个数为16,最多,
∴众数=6吨,
∵一共50个数据,最中间的数据为第25和第26个数据,
∴中位数=(6+6)÷2=6吨.
答: 这组月均用水量数据的平均数为5.9吨,众数为6吨,中位数为6吨.
【解析】【解答】解:(Ⅰ)本次调查的家庭个数=8+12+16+10+4=50个,
m%=10÷50×100%=20%.
故答案为:50,20;
【分析】(Ⅰ)由条形图可知各个用水量的家庭个数,把所有家庭个数相加可求得本次调查的家庭个数,再用用水量为6.5吨的家庭个数除以总家庭个数,即可求出m的值;
(Ⅱ)利用加权平均数的计算公式,将数据代入公式计算即可求的组月均用水量数据的平均数,由条形统计图可知用水量6吨的家庭个数是16为最多,可求得众数,再由50个数据,最中间的数据为第25和第26个数据,将这两个数据求和再除以2,即可求出中位数.
20.【答案】解:整理数据:按如下分段整理样本数据并补全表格:
分析数据:补全下列表格中的统计量:
八年级的成绩较为稳定,理由:∵七年级的方差=24.2,八年级的方差=20.4,24.2>20.4,∴八年级的成绩较为稳定.
故答案为:1,1,93.5,94.
【解析】【分析】根据中位数,众数和方差的定义即可得到结论.
21.【答案】(1)解:这7天内小申家每天用水量的平均数为==800(升)
将这7天的用水量从小到大重新排列为:780,785,790,800,805,815,825,∴用水量的中位数为800升。
(2)解:×100%=12.5%,答:第3天小申家洗衣服的水占这一天总用水量的百分比为12.5%。
(3)解:答案不唯一,例如:小申家冲厕所的用水量较大,可以用洗衣服的水冲厕所。采用以上建议,每天可节约用水100升,一个月估计可以节约用水100×30=3000(升)。
【解析】【分析】(1)根据平均数和中位数的定义进行计算即可求得;
(2)用洗衣服的水量除以第三天的用水总量即可求得;
(3)根据条形图给出节水的合理性建议均可,例如将洗衣服后的水用为冲厕所等.
22.【答案】(1)解:∵一共抽查了20个人,∴中位数等于第十个和第十一个学生评分的平均数;由图可知,第十个人评分8分,第十一个人平分9分;∴中位数=;由图可知,评分为9分的人数最多;∴众数是9
(2)解:评分为10分的人数所占百分比=1-10%-20%-15%-20%=35%=0.35∴平均数=,答:电影《水门桥》得分的平均数是8.5;
(3)解:抽出的20人中,《长津湖》得到满分的有4个,《水门桥》得到满分的有(个),所以(个).答:这两部作品一共可以得到110个满分.
【解析】【分析】(1)利用中位数和众数的定义及计算方法求解即可;
(2)利用平均数的计算方法求解即可;
(3)分别求出《长津湖》和《水门桥》的人数,再相加即可。
23.【答案】(1)解:根据图表上点的坐标为:(2,120),(2,200),
∴汽车的速度为 60千米/时,火车的速度为 100千米/时.
(2)解:依据题意得出:
y汽=240×2x+×5x+200=500x+200;
y火=240×1.6x+×5x+2280=396x+2280.
若y 汽>y 火,得出500x+200>396x+2280.
∴x>20;
(3)解:上周货运量=(17+20+19+22+22+23+24)÷7=21>20,
从平均数分析,建议预定火车费用较省.
从折线图走势分析,上周货运量周四(含周四)后大于20且呈上升趋势,
建议预订火车费用较省.
【解析】【分析】(1)根据图象可得火车2小时行驶的路程为200千米,汽车2小时行驶的路程为120千米,然后根据路程÷时间=速度进行求解;
(2)根据AB两地的距离×汽车的运费+AB两地的距离÷汽车的速度×冷藏价格+固定费用可得y汽与x的关系式;根据AB两地的距离×汽车的运费+AB两地的距离÷火车的速度×冷藏价格+固定费用可得y火与x的关系式,然后令y汽>y火,求出x的范围即可;
(3)根据平均数的计算方法求出上周货运的平均数,然后根据平均数的大小以及折线统计图的趋势进行分析判断.
24.【答案】(1)2;78.5;80
(2)解:∵七年级同学测试成绩的方差是66.6, 八年级同学测试成绩的方差是33,
∴,
∴估计八年级学生的竞赛成绩更整齐些.
(3)解:由题意得(人),
∴这两个年级竞赛成绩达到优秀学生的人数共约60人.
(4)解:可以推断出八年级学生的数学水平较高,
理由为两班平均数相同,八年级的中位数高于七年级;八年级的众数高于七年级,
说明八年级学生的竞赛成绩更好(答案不唯一).
【解析】【解答】(1)解:将七年级抽样成绩重新排列为:69,72,72,75,78,79,84,85,91,95,其中在90≤x<100范围内的数据有2个,
故a=2.
中位为b=(分),
将八年级的成绩出现次数最多是80分,共出现2次,
∴众数c=80(分),
故答案为:2,78.5,80;
【分析】(1)根据题干中的数据求出a的值,再利用众数和中位数的定义求出b、c的值即可;
(2)利用方差的定义及计算方法求解即可;
(3)先求出两个班“优秀”的人数,再相加即可;
(4)根据平均数和中位数的性质求解即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
