浙教版数学八年级下册 2.2一元二次方程的解法小结(共14张PPT)
文档属性
| 名称 | 浙教版数学八年级下册 2.2一元二次方程的解法小结(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 22:33:55 | ||
图片预览






文档简介
(共15张PPT)
①因式分解法
②开平方法
③配方法
④公式法
(方程一边是0,另一边整式容易因式分解)
( (x+m)2=k k≥0 )
(化方程为一般式)
(二次项系数为1,而一次项系数为偶数)
解一元二次方程的方法
方法1
方法2
方法3
解:移项,得
方程左边因式分解,得
①方程右边为零
解题步骤
用因式分解法解
②方程左边因式分解成A.B=0的形式
③A=0或B=0
④写出方程的两个根
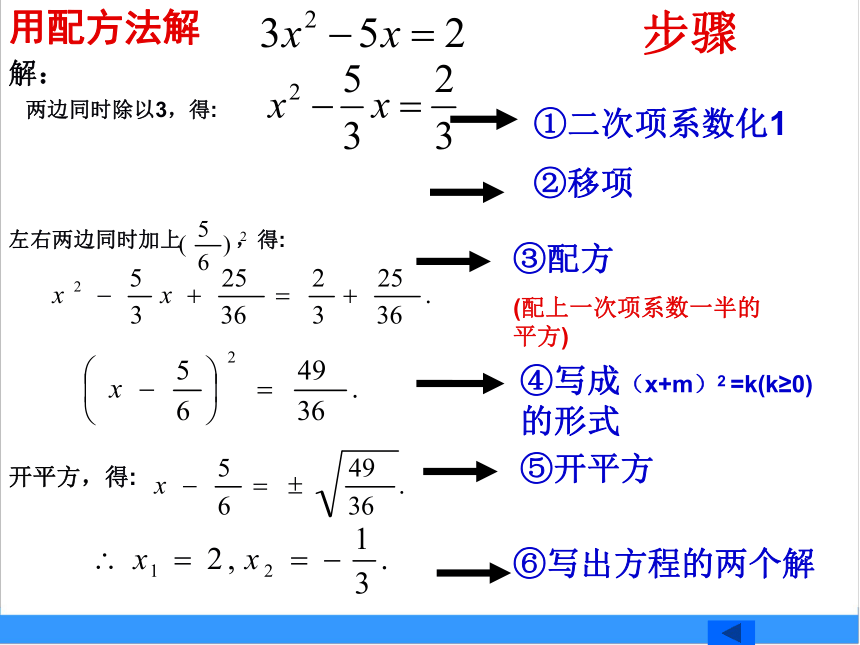
用配方法解
解:
两边同时除以3,得:
左右两边同时加上 ,得:
开平方,得:
①二次项系数化1
步骤
②移项
③配方
(配上一次项系数一半的平方)
④写成(x+m)2 =k(k≥0) 的形式
⑤开平方
⑥写出方程的两个解
用公式法解
解:移项,得
这里a=3,b=-5,c=-2
=49
解题步骤
①将方程化成一般式,并写出a,b,c
②求出b2-4ac的值
(特别注意b2-4ac<0)
③代入求根公式
④写出方程的两个根
例1.选择适当的方法解下列方程:
①
②
③
先考虑开平方法,
再用因式分解法;
最后才用公式法和配方法.
请你选择恰当的方法解方程
① (x-1)(x+1)=x
② x (2x+5)=2 (2x+5)
③ (2x-1)2=4(x+3)2
④ 3(x-2)2-9=0
能不能用整体
思想?
例2. 解方程
② 2(x-2)2+5(x-2)-3=0
总结:方程中有括号时,应先用整体思想考虑有没有简单方法,若看不出合适的方法时,则把它去括号并整理为一般形式再选取合理的方法。
变1: 2(x-2)2+5(2-x)-3=0
再变为: 2(x-2)2+5x-13=0
2(x-2)2+5x-10-3=0
变2: 2(2-x)2+5(2-x)-3=0
① (2m+3)2=2(4m+7)
2(x-2)2+5(x-2)-3=0
比一比谁最快:
① (y+ )(y- )=2(2y-3)
② 3t(t+2)=2(t+2)
③ x2=4 x-11
④ (x+101)2-10(x+101)+9=0
y1=y2=2
t1=-2,t2=2/3
x1= , x2=
x1=-92,x2=-100
能力拓展
解关于x的方程:
①
②
小结:
ax2=c (c≥0) ====>
ax2+bx=0 ====>
ax2+bx+c=0 ====>
因式分解法
公式法(配方法)
2、公式法虽然是万能的,对任何一元二次方程都适用,但不一定 是最简单的,因此在解方程时我们首先考虑能否应用“直接开平方法”、“因式分解法”等简单方法,若不行,再考虑公式法(适当也可考虑配方法)
3、方程中有括号时,应先用整体思想考虑有没有简单方法,若看不出合适的方法时,则把它去括号并整理为一般形式再选取合理的方法。
1、
直接开平方法
因式分解法
结束寄语
配方法和公式法是解一元二次方程重要方法,要作为一种基本技能来掌握.
一元二次方程也是刻画现实世界的有效数学模型.
①因式分解法
②开平方法
③配方法
④公式法
(方程一边是0,另一边整式容易因式分解)
( (x+m)2=k k≥0 )
(化方程为一般式)
(二次项系数为1,而一次项系数为偶数)
解一元二次方程的方法
方法1
方法2
方法3
解:移项,得
方程左边因式分解,得
①方程右边为零
解题步骤
用因式分解法解
②方程左边因式分解成A.B=0的形式
③A=0或B=0
④写出方程的两个根
用配方法解
解:
两边同时除以3,得:
左右两边同时加上 ,得:
开平方,得:
①二次项系数化1
步骤
②移项
③配方
(配上一次项系数一半的平方)
④写成(x+m)2 =k(k≥0) 的形式
⑤开平方
⑥写出方程的两个解
用公式法解
解:移项,得
这里a=3,b=-5,c=-2
=49
解题步骤
①将方程化成一般式,并写出a,b,c
②求出b2-4ac的值
(特别注意b2-4ac<0)
③代入求根公式
④写出方程的两个根
例1.选择适当的方法解下列方程:
①
②
③
先考虑开平方法,
再用因式分解法;
最后才用公式法和配方法.
请你选择恰当的方法解方程
① (x-1)(x+1)=x
② x (2x+5)=2 (2x+5)
③ (2x-1)2=4(x+3)2
④ 3(x-2)2-9=0
能不能用整体
思想?
例2. 解方程
② 2(x-2)2+5(x-2)-3=0
总结:方程中有括号时,应先用整体思想考虑有没有简单方法,若看不出合适的方法时,则把它去括号并整理为一般形式再选取合理的方法。
变1: 2(x-2)2+5(2-x)-3=0
再变为: 2(x-2)2+5x-13=0
2(x-2)2+5x-10-3=0
变2: 2(2-x)2+5(2-x)-3=0
① (2m+3)2=2(4m+7)
2(x-2)2+5(x-2)-3=0
比一比谁最快:
① (y+ )(y- )=2(2y-3)
② 3t(t+2)=2(t+2)
③ x2=4 x-11
④ (x+101)2-10(x+101)+9=0
y1=y2=2
t1=-2,t2=2/3
x1= , x2=
x1=-92,x2=-100
能力拓展
解关于x的方程:
①
②
小结:
ax2=c (c≥0) ====>
ax2+bx=0 ====>
ax2+bx+c=0 ====>
因式分解法
公式法(配方法)
2、公式法虽然是万能的,对任何一元二次方程都适用,但不一定 是最简单的,因此在解方程时我们首先考虑能否应用“直接开平方法”、“因式分解法”等简单方法,若不行,再考虑公式法(适当也可考虑配方法)
3、方程中有括号时,应先用整体思想考虑有没有简单方法,若看不出合适的方法时,则把它去括号并整理为一般形式再选取合理的方法。
1、
直接开平方法
因式分解法
结束寄语
配方法和公式法是解一元二次方程重要方法,要作为一种基本技能来掌握.
一元二次方程也是刻画现实世界的有效数学模型.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
