浙教版数学九年级上册 第3章 圆的基本性质复习课件(15张PPT)
文档属性
| 名称 | 浙教版数学九年级上册 第3章 圆的基本性质复习课件(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-18 23:00:10 | ||
图片预览



文档简介
(共15张PPT)
同学,你好!
白岩松——中央电视台主持人
湖州不大不小,幸福正好!
家乡之美
一切立体图形中最美的是球,
—— 毕达哥拉斯
古希腊
一切平面图形中最美的是圆.
圆的基本性质复习
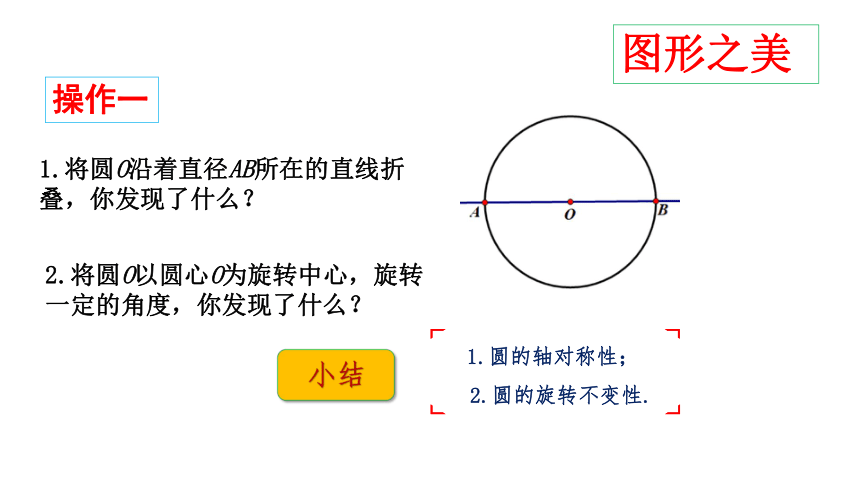
操作一
1.将圆O沿着直径AB所在的直线折叠,你发现了什么?
2.将圆O以圆心O为旋转中心,旋转一定的角度,你发现了什么?
1.圆的轴对称性;
2.圆的旋转不变性.
小结
图形之美
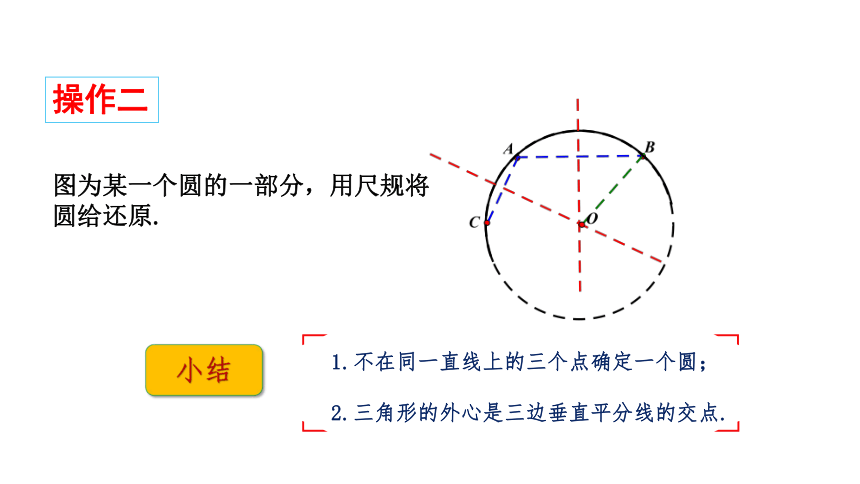
操作二
图为某一个圆的一部分,用尺规将圆给还原.
小结
1.不在同一直线上的三个点确定一个圆;
2.三角形的外心是三边垂直平分线的交点.
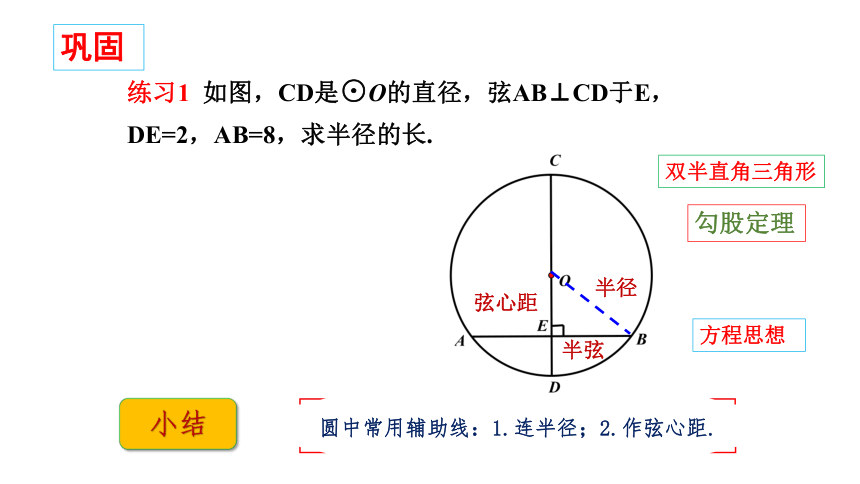
练习1 如图,CD是⊙O的直径,弦AB⊥CD于E,DE=2,AB=8,求半径的长.
双半直角三角形
半径
半弦
弦心距
勾股定理
小结
圆中常用辅助线:1.连半径;2.作弦心距.
方程思想
巩固
2或8
变式1 在半径为5 cm的圆O中,如果弦AB=8 cm, 直径CD⊥AB,垂足为点E,则DE的长为________cm.
?
分类讨论思想
练习2 如图,△ABC是圆内接三角形,AB=10,圆周角∠C = 45 °,求圆O的直径.
直径直角三角形
双半直角三角形
拓展
变式1 如图,△ABC是圆内接三角形,AB=10,圆周角∠C = 60 °,求圆O的直径.
类比思想
转化思想
追问:观察两黄色图形,
找出其中的联系.
变式2
△ABC是圆内接三角形,弦AB=10,圆O的半径是10,求∠C.
30 °或150 °
变式3 创造
△ABC是圆内接三角形,弦AB=10,当圆O的半径=____时,∠C=____.
思维之美
练习3 已知等边△ABC内接于⊙O.点P为 上的一个动点,连结PA、PB、PC.
(1)如图1,当线段PC经过点O时,试写出线段PA,PB,PC之间满足的等量关系,并说明理由;
解法一
D
截长法
(2)如图2,点P为 圆上的任意一点(点P不与点A、点B重合),试探究线段PA,PB,PC之间满足的等量关系,并证明你的结论.
“截长补短”法
“手拉手”(绕A)
旋转
转化
课后反思:1.还可以怎么“截长”?
2.可否“补短”?
圆的基本性质
辅助线
连半径
作弦心距
数学思想
转化思想
方程思想
分类讨论
类比思想
基本定理
圆心角定理
垂径定理
圆周角定理
作直径 构直角
构造双半直角三角形
构造直径直角三角形
基本经验
感悟提升
同学,你好!
白岩松——中央电视台主持人
湖州不大不小,幸福正好!
家乡之美
一切立体图形中最美的是球,
—— 毕达哥拉斯
古希腊
一切平面图形中最美的是圆.
圆的基本性质复习
操作一
1.将圆O沿着直径AB所在的直线折叠,你发现了什么?
2.将圆O以圆心O为旋转中心,旋转一定的角度,你发现了什么?
1.圆的轴对称性;
2.圆的旋转不变性.
小结
图形之美
操作二
图为某一个圆的一部分,用尺规将圆给还原.
小结
1.不在同一直线上的三个点确定一个圆;
2.三角形的外心是三边垂直平分线的交点.
练习1 如图,CD是⊙O的直径,弦AB⊥CD于E,DE=2,AB=8,求半径的长.
双半直角三角形
半径
半弦
弦心距
勾股定理
小结
圆中常用辅助线:1.连半径;2.作弦心距.
方程思想
巩固
2或8
变式1 在半径为5 cm的圆O中,如果弦AB=8 cm, 直径CD⊥AB,垂足为点E,则DE的长为________cm.
?
分类讨论思想
练习2 如图,△ABC是圆内接三角形,AB=10,圆周角∠C = 45 °,求圆O的直径.
直径直角三角形
双半直角三角形
拓展
变式1 如图,△ABC是圆内接三角形,AB=10,圆周角∠C = 60 °,求圆O的直径.
类比思想
转化思想
追问:观察两黄色图形,
找出其中的联系.
变式2
△ABC是圆内接三角形,弦AB=10,圆O的半径是10,求∠C.
30 °或150 °
变式3 创造
△ABC是圆内接三角形,弦AB=10,当圆O的半径=____时,∠C=____.
思维之美
练习3 已知等边△ABC内接于⊙O.点P为 上的一个动点,连结PA、PB、PC.
(1)如图1,当线段PC经过点O时,试写出线段PA,PB,PC之间满足的等量关系,并说明理由;
解法一
D
截长法
(2)如图2,点P为 圆上的任意一点(点P不与点A、点B重合),试探究线段PA,PB,PC之间满足的等量关系,并证明你的结论.
“截长补短”法
“手拉手”(绕A)
旋转
转化
课后反思:1.还可以怎么“截长”?
2.可否“补短”?
圆的基本性质
辅助线
连半径
作弦心距
数学思想
转化思想
方程思想
分类讨论
类比思想
基本定理
圆心角定理
垂径定理
圆周角定理
作直径 构直角
构造双半直角三角形
构造直径直角三角形
基本经验
感悟提升
同课章节目录
