4.2 平行四边形及其性质(3)课件(共18张PPT)
文档属性
| 名称 | 4.2 平行四边形及其性质(3)课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 443.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-19 00:00:00 | ||
图片预览

文档简介
(共18张PPT)
n边形的内角和为(n-2)×180°(n≥3)
n边形的对角线和为 (n-3)×n÷2
A1
A2
A3
A4
A5
A6
A7
An
1.从多边形的一个顶点 A1 处引出(n-3)条对角线,
分割出(n-2)个三角形
温故知新:
A1
A2
A3
A4
A5
A6
A7
An
⌒
4
A
B
C
D
E
⌒
1
⌒
2
⌒
3
⌒
5
.
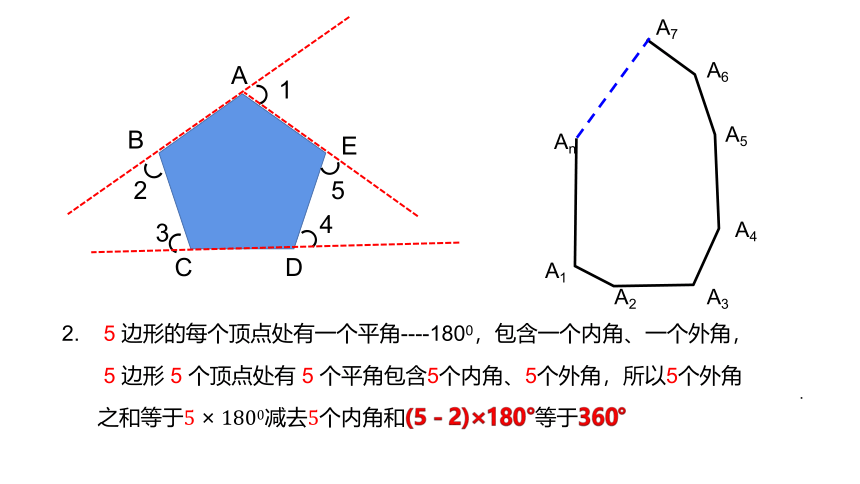
2. 5 边形的每个顶点处有一个平角----1800,包含一个内角、一个外角,
5 边形 5 个顶点处有 5 个平角包含5个内角、5个外角,所以5个外角
之和等于个内角和(5-2)×180°等于360°
.
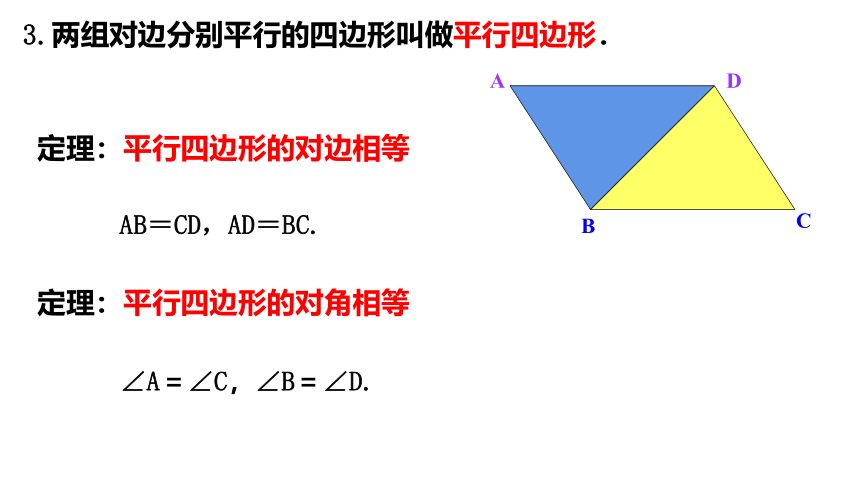
3.两组对边分别平行的四边形叫做平行四边形.
D
C
B
A
定理:平行四边形的对边相等
AB=CD,AD=BC.
定理:平行四边形的对角相等
∠A=∠C,∠B=∠D.
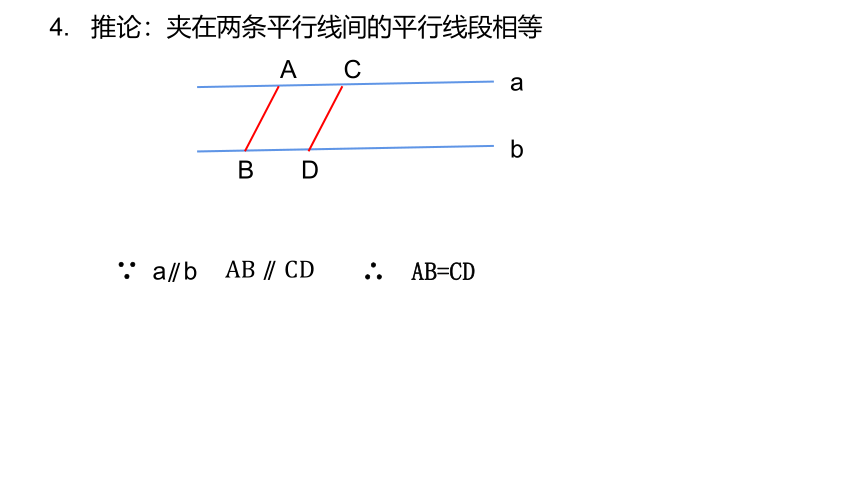
4. 推论:夹在两条平行线间的平行线段相等
a
b
A
B
C
D
∴ AB=CD
AB ∥ CD
∵ a∥ b
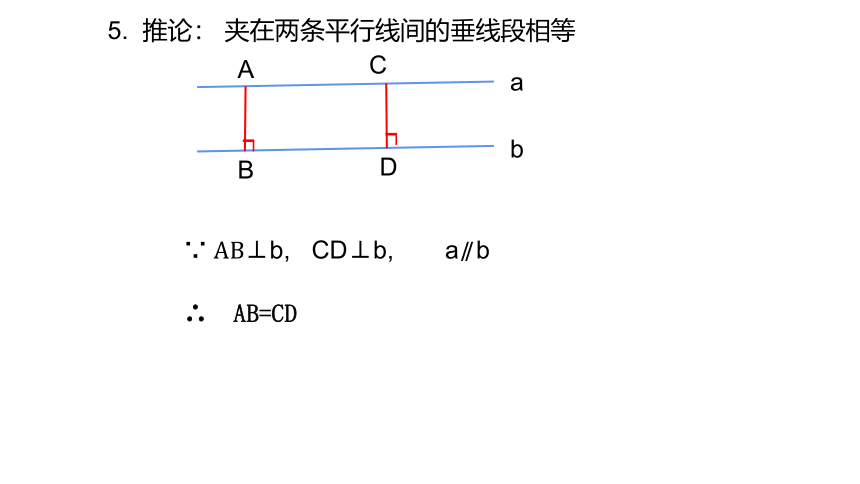
5. 推论: 夹在两条平行线间的垂线段相等
a
b
∴ AB=CD
a∥ b
A
B
┎
C
D
┎
∵ AB⊥b, CD⊥b,
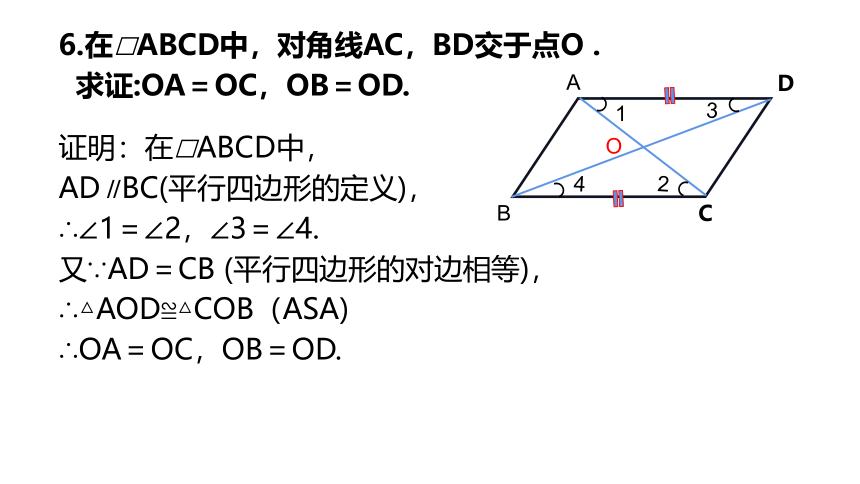
6.在□ABCD中,对角线AC,BD交于点O .
求证:OA=OC,OB=OD.
证明:在□ABCD中,
AD∥BC(平行四边形的定义),
∴∠1=∠2,∠3=∠4.
又∵AD=CB (平行四边形的对边相等),
∴△AOD≌△COB(ASA)
∴OA=OC,OB=OD.
A
B
C
D
O
⌒
1
⌒
2
⌒
3
⌒
4
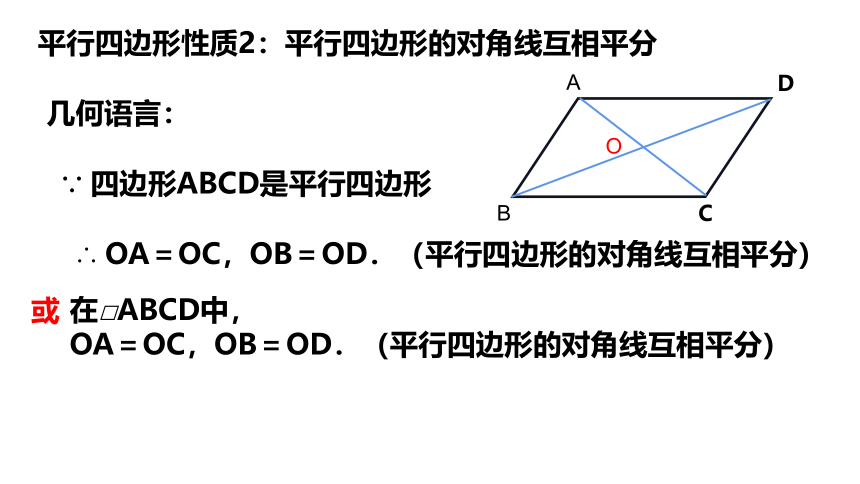
几何语言:
平行四边形性质2:平行四边形的对角线互相平分
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD.(平行四边形的对角线互相平分)
或
在□ABCD中,
OA=OC,OB=OD.(平行四边形的对角线互相平分)
A
B
C
D
O
例3 如图,□ABCD的对角线AC,BD交于点O.过点O作直线EF,分别交AB,CD于点E,F.
求证:OE=OF.
证明:在□ABCD中,
AB∥CD(平行四边形的定义),
∴∠1=∠2,
又∵OA=OC (平行四边形的对角线互相平分),∠3=∠4
∴△AOE≌△COF.
∴OE=OF.
A
B
C
D
O
F
E
⌒
1
⌒
2
⌒
3
⌒
4
A
B
C
D
O
F
E
⌒
1
⌒
2
⌒
3
⌒
4
证明:过平行四边形对角线交点的任意一条直线都
将这个平行四边形分成面积相等的两部分.
△AOE≌△COF
分析:
△AOD≌△COB
△DOF≌△BOE
S△AOE=S△COF
S△AOD=S△COB
S△DOF=S△BOE
S△AOE+S△AOD +S△DOF=S△COF+S△COB+S△BOE
S四边形AEFD =S四边形EBCF
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分
让EF绕点O旋转:
例4 如图,在□ABCD中,对角线AC,BD交于点E,AC⊥BC.若 AC=4,AB=5,求BD的长.
解:∵ AC⊥BC
∵ 四边形ABCD是平行四边形
(平行四边形对角线互相平分)
∴CE= AC=2,BD=2BE
∴BD=2BE=
┎
F
法2:BD=2
.
∴BC===3
.
归纳小结:
平行四边形及其性质:
从边看:平行四边形的对边平行且相等;
从角看:平行四边形的对角相等,邻角互补;
从对角线看:平行四边形的对角线互相平分
从对角线交点从看:
过平行四边形对角线交点的任意一条直线
都将这个平行四边形分成面积相等的两部分.
一分钟背诵
1.如图:在 ABCD中,对角线AC,BD相交于点O.如果BD=12,AC=10,BC=m,那么m的取值范围是 ( )
C
A.10当堂检测:
夯实基础,稳扎稳打
2.已知:如图,在□ABCD中,对角线AC,BD交于点O,点E,F分别在AO,CO上,且AE=CF. 求证:∠EBO =∠FDO.
证明:
在 ABCD中,
OB= OD,0A = OC
∵AE=CF,
∴ 0E= OF (等量减等量,其差相等)
.
⌒
1
⌒
2
∴
∴∠EBO =∠FDO
3.如图: 在 ABCD中,BD⊥AB,AB=12 cm,AC=26 cm,求BD,AD的长.
4.平行四边形被两条对角线分成四个小三角形,每个小三角
形的面积_________,等于平行四边形面积的________.
相等
连续递推,豁然开朗
5.如图, ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么 ABCD的周长是 .
16
分析:中线+垂线=等腰三角形
6、一块草地中间有一水井,为了浇水的方便,经过水井修一条小路,并且把草地分成面积相等的两部分,同学们,你能画出小路的位置吗?
B
M
C
●
D
A
O
思维拓展,更上一层
注: 过平行四边形对角线交点的任意一条直线
都将这个平行四边形分成面积相等的两部分.
n边形的内角和为(n-2)×180°(n≥3)
n边形的对角线和为 (n-3)×n÷2
A1
A2
A3
A4
A5
A6
A7
An
1.从多边形的一个顶点 A1 处引出(n-3)条对角线,
分割出(n-2)个三角形
温故知新:
A1
A2
A3
A4
A5
A6
A7
An
⌒
4
A
B
C
D
E
⌒
1
⌒
2
⌒
3
⌒
5
.
2. 5 边形的每个顶点处有一个平角----1800,包含一个内角、一个外角,
5 边形 5 个顶点处有 5 个平角包含5个内角、5个外角,所以5个外角
之和等于个内角和(5-2)×180°等于360°
.
3.两组对边分别平行的四边形叫做平行四边形.
D
C
B
A
定理:平行四边形的对边相等
AB=CD,AD=BC.
定理:平行四边形的对角相等
∠A=∠C,∠B=∠D.
4. 推论:夹在两条平行线间的平行线段相等
a
b
A
B
C
D
∴ AB=CD
AB ∥ CD
∵ a∥ b
5. 推论: 夹在两条平行线间的垂线段相等
a
b
∴ AB=CD
a∥ b
A
B
┎
C
D
┎
∵ AB⊥b, CD⊥b,
6.在□ABCD中,对角线AC,BD交于点O .
求证:OA=OC,OB=OD.
证明:在□ABCD中,
AD∥BC(平行四边形的定义),
∴∠1=∠2,∠3=∠4.
又∵AD=CB (平行四边形的对边相等),
∴△AOD≌△COB(ASA)
∴OA=OC,OB=OD.
A
B
C
D
O
⌒
1
⌒
2
⌒
3
⌒
4
几何语言:
平行四边形性质2:平行四边形的对角线互相平分
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD.(平行四边形的对角线互相平分)
或
在□ABCD中,
OA=OC,OB=OD.(平行四边形的对角线互相平分)
A
B
C
D
O
例3 如图,□ABCD的对角线AC,BD交于点O.过点O作直线EF,分别交AB,CD于点E,F.
求证:OE=OF.
证明:在□ABCD中,
AB∥CD(平行四边形的定义),
∴∠1=∠2,
又∵OA=OC (平行四边形的对角线互相平分),∠3=∠4
∴△AOE≌△COF.
∴OE=OF.
A
B
C
D
O
F
E
⌒
1
⌒
2
⌒
3
⌒
4
A
B
C
D
O
F
E
⌒
1
⌒
2
⌒
3
⌒
4
证明:过平行四边形对角线交点的任意一条直线都
将这个平行四边形分成面积相等的两部分.
△AOE≌△COF
分析:
△AOD≌△COB
△DOF≌△BOE
S△AOE=S△COF
S△AOD=S△COB
S△DOF=S△BOE
S△AOE+S△AOD +S△DOF=S△COF+S△COB+S△BOE
S四边形AEFD =S四边形EBCF
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分
让EF绕点O旋转:
例4 如图,在□ABCD中,对角线AC,BD交于点E,AC⊥BC.若 AC=4,AB=5,求BD的长.
解:∵ AC⊥BC
∵ 四边形ABCD是平行四边形
(平行四边形对角线互相平分)
∴CE= AC=2,BD=2BE
∴BD=2BE=
┎
F
法2:BD=2
.
∴BC===3
.
归纳小结:
平行四边形及其性质:
从边看:平行四边形的对边平行且相等;
从角看:平行四边形的对角相等,邻角互补;
从对角线看:平行四边形的对角线互相平分
从对角线交点从看:
过平行四边形对角线交点的任意一条直线
都将这个平行四边形分成面积相等的两部分.
一分钟背诵
1.如图:在 ABCD中,对角线AC,BD相交于点O.如果BD=12,AC=10,BC=m,那么m的取值范围是 ( )
C
A.10
夯实基础,稳扎稳打
2.已知:如图,在□ABCD中,对角线AC,BD交于点O,点E,F分别在AO,CO上,且AE=CF. 求证:∠EBO =∠FDO.
证明:
在 ABCD中,
OB= OD,0A = OC
∵AE=CF,
∴ 0E= OF (等量减等量,其差相等)
.
⌒
1
⌒
2
∴
∴∠EBO =∠FDO
3.如图: 在 ABCD中,BD⊥AB,AB=12 cm,AC=26 cm,求BD,AD的长.
4.平行四边形被两条对角线分成四个小三角形,每个小三角
形的面积_________,等于平行四边形面积的________.
相等
连续递推,豁然开朗
5.如图, ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为8,那么 ABCD的周长是 .
16
分析:中线+垂线=等腰三角形
6、一块草地中间有一水井,为了浇水的方便,经过水井修一条小路,并且把草地分成面积相等的两部分,同学们,你能画出小路的位置吗?
B
M
C
●
D
A
O
思维拓展,更上一层
注: 过平行四边形对角线交点的任意一条直线
都将这个平行四边形分成面积相等的两部分.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
