第六章 反比例函数复习课(2)

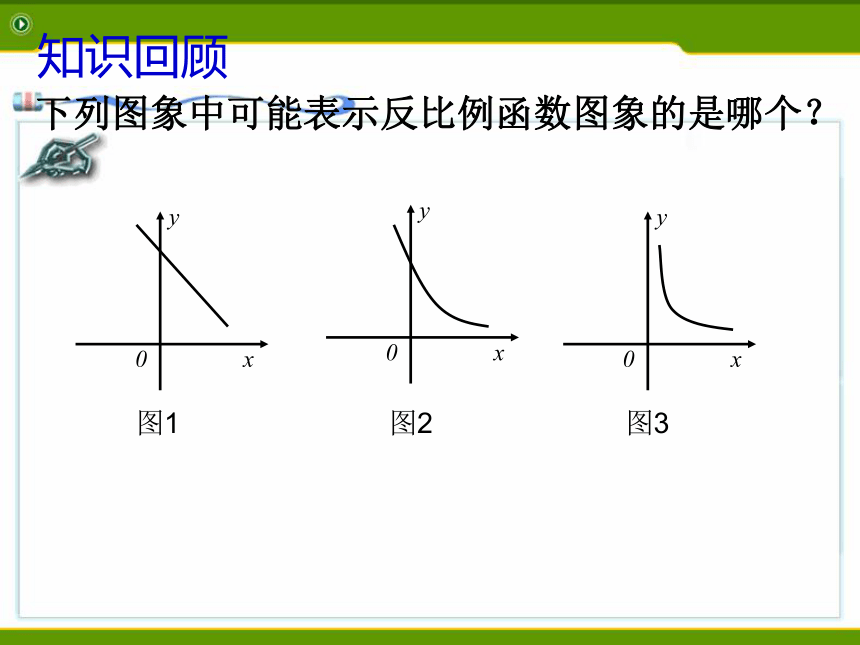
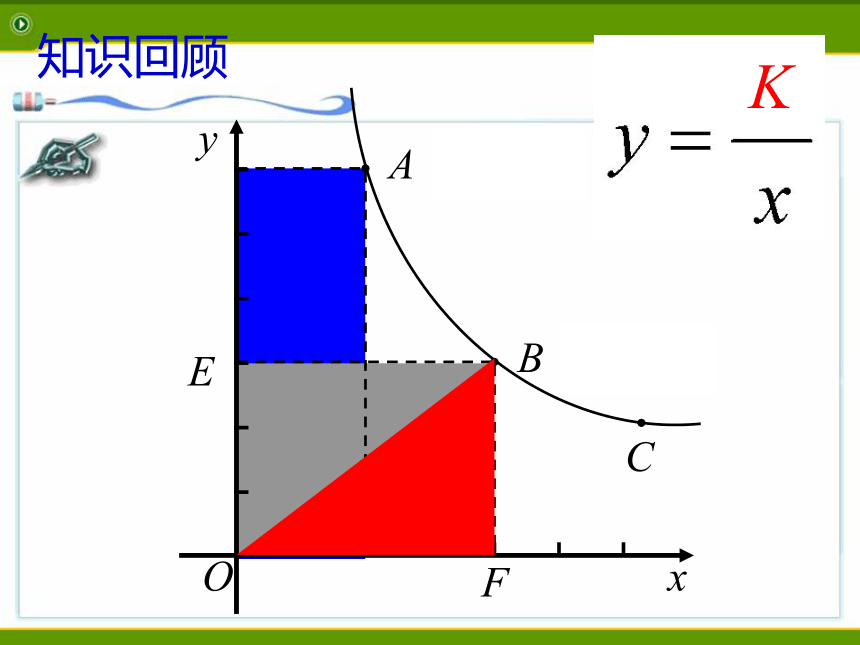
课件23张PPT。反比例函数复习课––面积问题––表1表2表3下列哪一个可能表示反比例函数？知识回顾下列图象中可能表示反比例函数图象的是哪个？0xy图10xy图20xy图3知识回顾知识回顾OK
EF4
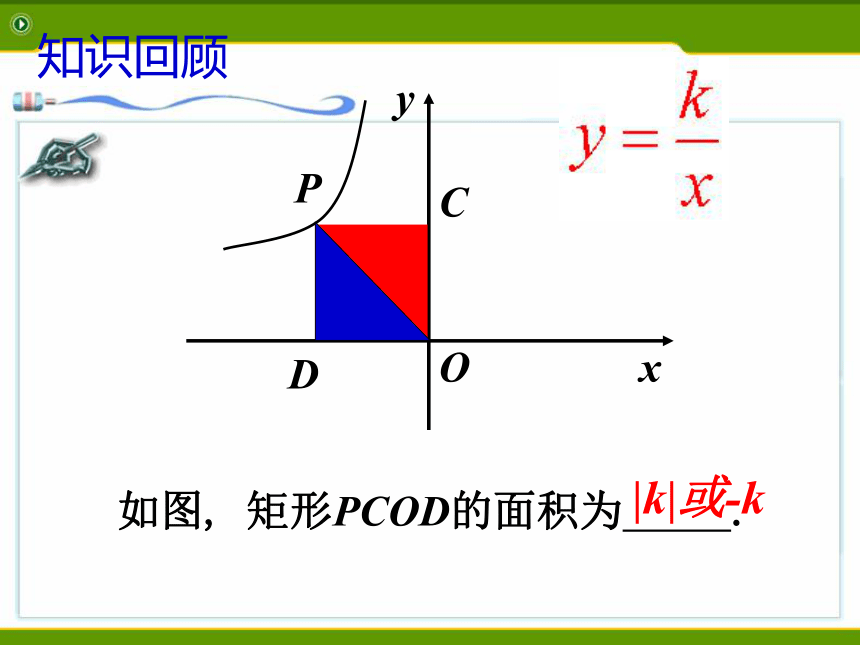
如图, 矩形PCOD的面积为 .xyPDC|k|或-kO知识回顾1、如图,点A为双曲线 上一点,过点
A分别作坐标轴的垂线段,垂足分别为
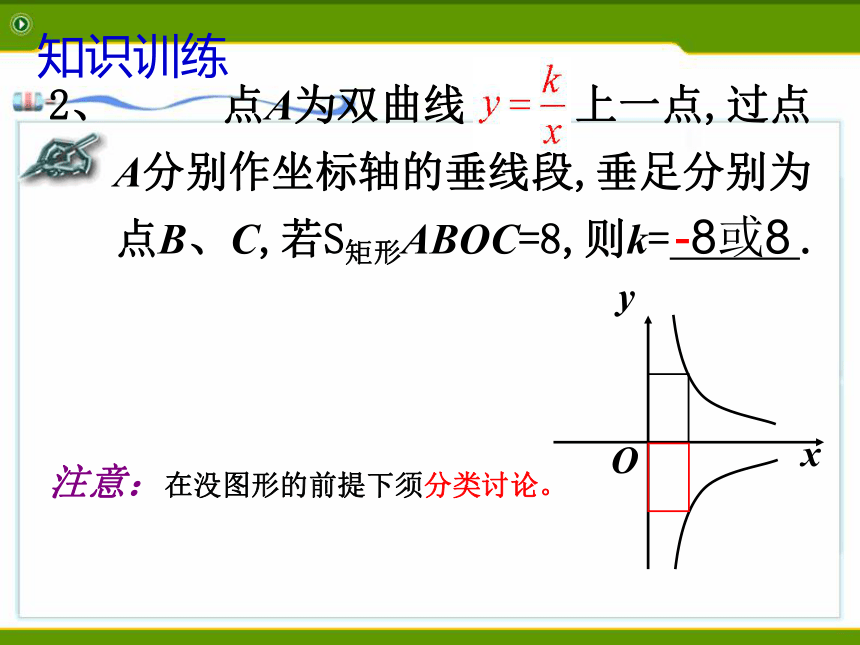
点B、C,若S矩形ABOC=8,则k= .-8知识训练CBOAxy2、 点A为双曲线 上一点,过点
A分别作坐标轴的垂线段,垂足分别为
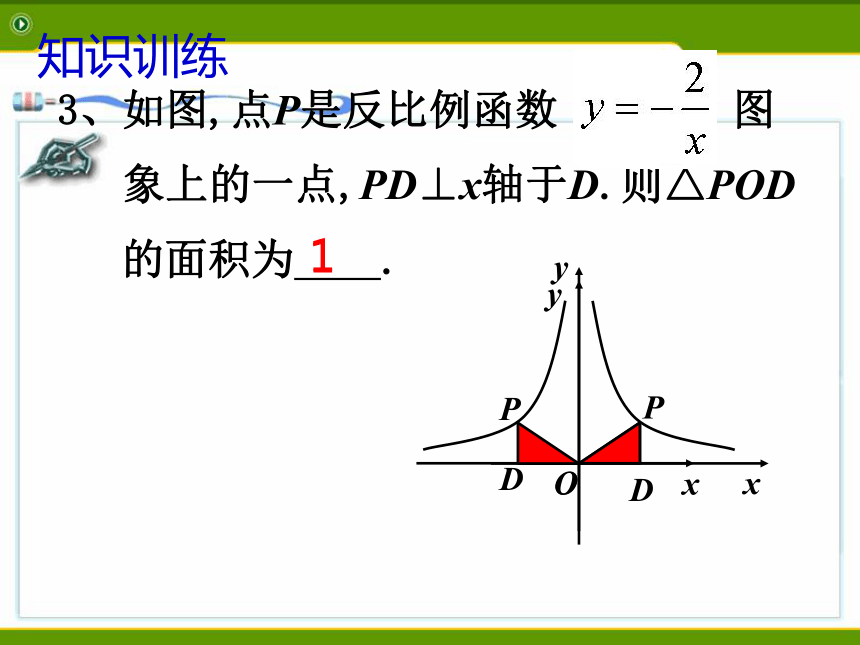
点B、C,若S矩形ABOC=8,则k= .注意：在没图形的前提下须分类讨论。-8或8知识训练3、如图,点P是反比例函数 图
象上的一点,PD⊥x轴于D.则△POD
的面积为 .11知识训练4.如图,P是反比例函数 在第一象限
分支上的一个动点,PA⊥x轴于点A,随着
P点的横坐标逐渐增大,△APO的面积将
（ ）
A.增大 B.减小
C.不变 D.无法确定 C知识训练5.如图,P是反比例函数 在第一象限
分支上的一个动点, 点A是x轴正半轴上
的一个定点, 当点P的横坐标逐渐增大
时,△OAP的面积将会（ ）
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小 PAOyxC知识训练6.如图,双曲线 与 在第一象限内
如图所示，作一条平行于y轴的直线分别
交双曲线于A，B两点，连接OA，OB，
求△AOB的面积.ABOyxC知识训练7、函数 和 在第一象限内的
图象如图，点P是 的图象上一动
点，PA⊥x轴于点A，PB⊥y轴交
的图象于点B.求图中阴影部分的面积. 知识训练PAB8、如图，在x轴的正半轴上依次截取OA1=A1A2=A2A3=
A3A4=A4A5，过点A1,A2,A3,A4,A5分别作x轴的垂线
与反比例函数 的图象相交得直角三角形OP1A1,
A1P2A2,A2P3A3,A3P4A4,A4P5A5,并设其面积分别为
S1,S2,S3,S4,S5,则S5的值为 ．拓展提升yxOP1P2P3P4P5 A1 A2 A3 A4 A58、如图，在x轴的正半轴上依次截取OA1=A1A2=A2A3=
A3A4=A4A5，过点A1,A2,A3,A4,A5分别作x轴的垂线
与反比例函数 的图象相交得直角三角形OP1A1,
A1P2A2,A2P3A3,A3P4A4,A4P5A5,并设其面积分别为
S1,S2,S3,S4,S5,则S5的值为 ．拓展提升8、如图，在x轴的正半轴上依次截取OA1=A1A2=A2A3=
A3A4=A4A5，过点A1,A2,A3,A4,A5分别作x轴的垂线
与反比例函数 的图象相交得直角三角形OP1A1,
A1P2A2,A2P3A3,A3P4A4,A4P5A5,并设其面积分别为
S1,S2,S3,S4,S5,则S5的值为 ．拓展提升yxOP1P2P3P4P5 A1 A2 A3 A4 A5S1S3S5S1+S3+S5=拓展提升9、如图，P1、P2、P3、P4、P5是函数 的第一象限上的点， P1A1、P2A2、P3A3、P4A4、P5A5都垂直于x轴；在x轴上各相邻两点之间的距离均相等，求所有阴影部分的面积之和.O A1 B1 A2 B2 A3 B3 A4 B4 A5 B5 x10、如图，P1、P2、P3、P4、P5是函数
的第一象限上的点， P1A1、P2A2、P3A3、
P4A4、P5A5都垂直于x轴，OA1=A1A2=A2A3=
A3A4=A4A5，四边形A1P2B1A1、A2P3B2A2、
A3P4B3A3、A4P5B4A4是平行四边形，求所有阴
影部分的面积之和.拓展提升拓展提升ABC11、AB//x轴
BC//y轴E△12.如图，直线y=mx与双曲线 交
于A、B两点，过点A作AM⊥x轴，垂
足为M，连结BM,若 求k的值.学以致用13、如图,点M、A是反比例函数 图象
上的动点，过M点作直线MB∥x轴，交y轴
于B点；过A点作直线AC∥y轴，交x轴于C
点，交直线MB于D点.当四边形OADM的
面积为6时，说明线段BM与DM的大小关系.xABOCDMy学以致用14、如图，已知双曲线 经过Rt△OAB
斜边OB的中点D，与直角边AB相交于点C
若△OBC的面积为3，则k＝ ．学以致用15.已知:如图,反比例函数 与一次
函数y2=-x+2的图像交于A，B两点,求:
（1）A、B两点的坐标;
（2）△AOB的面积.
1（3） x的取何值时，y1>y2.反比例函数的面积不变性
反比例函数图象的对称性两种思想：数形结合和分类讨论总结提高两个性质：