第六章 反比例函数复习课(1)

课件15张PPT。反比例函数复习课复习回顾1、如果两个变量的积为一个 ，那么我们就说这两个变量成反比例。2、反比例函数y= （k≠0）的图象是由两个分支组成的曲线。
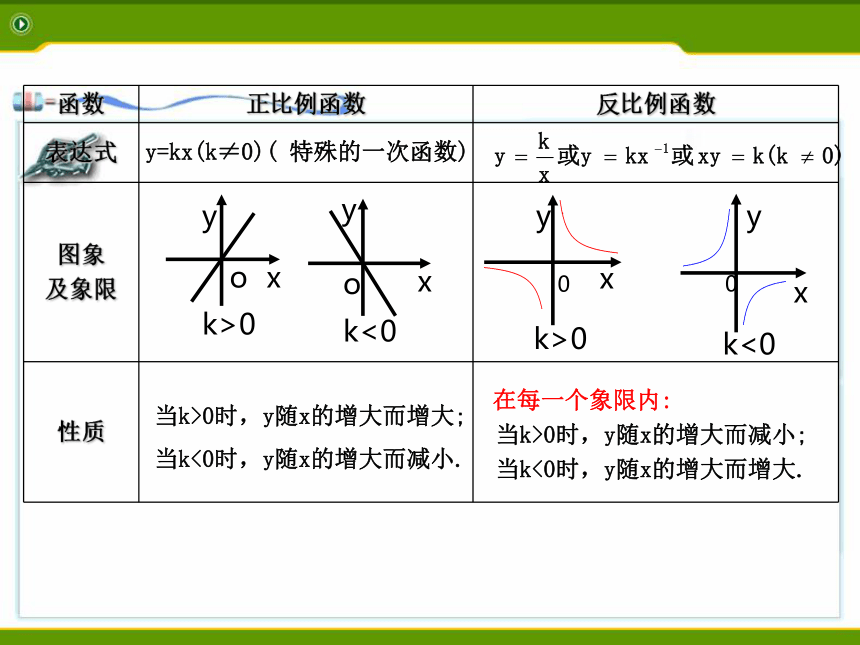
当k＞0时，函数图象在 、 象限，在每一象限内，y随x的增大而 ；
当k＜0时，函数图象在 、 象限，在每一象限内，y随x的增大而 。3、反比例函数y= （k≠0）的图象关于直角坐标系
的 成中心对称。不为零的常数一三减小二四增大原点在每一个象限内:
当k>0时，y随x的增大而减小;
当k<0时，y随x的增大而增大.y=kx(k≠0)( 特殊的一次函数)当k>0时，y随x的增大而增大;
当k<0时，y随x的增大而减小.互助质疑1、反比例函数y= ，当x= 2 时，函数y的值是 。
2、在电压为380伏特的条件下，电流I是电阻R的函数，它们的


关系式为 。
3、已知反比例函数y= 图象经过点（－2，4），则k的值
是 。-8-84、请写出一个图象位于第二、四象限的反比例函数解析
式： 。
5、已知反比例函数y= ，当x＞0时，y随着x的增大而
增大。则m的取值范围是 。
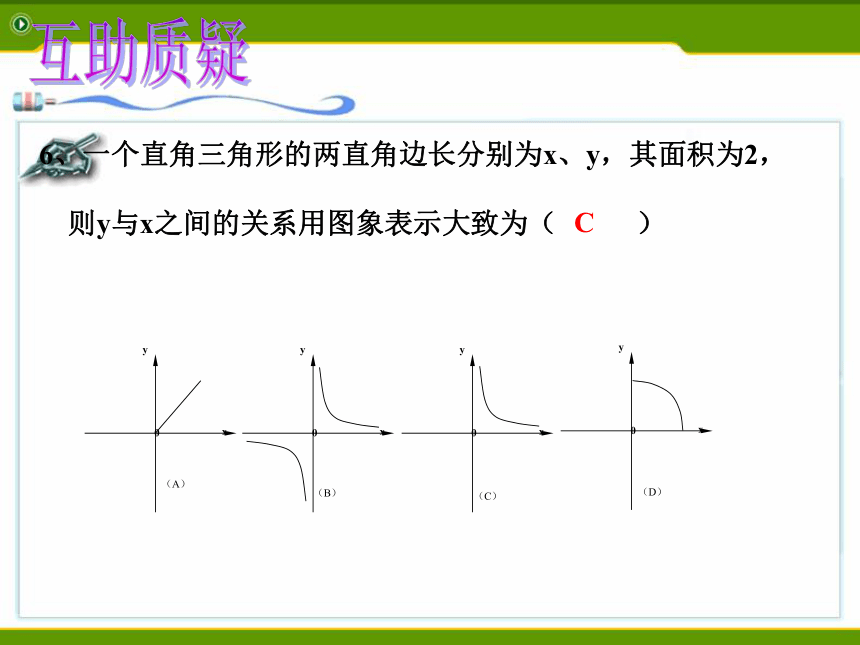
互助质疑互助质疑6、一个直角三角形的两直角边长分别为x、y，其面积为2，
则y与x之间的关系用图象表示大致为（ ）C互助质疑当x＞1时，求y的取值范围 。
当x<1时， 求y的取值范围 。
7、已知反比例函数 ，互助质疑8.如图,点P是反比例函数图象上的一点,过点P分别向x轴、

y轴作垂线,若阴影部分面积为3,则
这个反比例函数的关系式是 ;
9.已知反比例函数 (k≠0)，当x＜0时，y随x的增大而
减小，则一次函数y=kx-k的图象不经过第 象限互助质疑二10、已知反比例函数 ，若 ，
其对应值y1,y2 , 的大小关系是 。y3y1＜y3＜y2互助质疑互助质疑11、如图：一次函数y=kx+b的图象与反比例函数y=
的图象相交于点A（-2，1），与x轴交于点C（-1，0）。
①求该反比例函数和一次函数的解析式；
②求直线与反比例图像的另一交点B的坐标，
③连结OA、OB，求△AOB的面积。
④观察图像， 当x取何值时，
反比例函数的值 ，大于一次函数的值。1、在如图所示的矩形ABC中,AB=3,BC=4,
点P是BC边上与B,C不重合的点,设PA=x,D到PA的距离为y,求y关于x的解析式,并写出自变量x的取值范围.BACDPxy点拨拓展2、为了预防“流感”，某学校对教室采用
药熏消毒法进行消毒. 已知药物燃烧时，
室内每立方米空气中的含药量y（毫克）
与时间x(分钟）成正比例，药物燃烧完后，y与x成反比例（如图所示）. 现测得药物8分钟燃毕，此时室内空气中每立方米含药量为6毫克. 请根据题中所提供的信息，解答下列问题：
（1）药物燃烧时，y关于x的函数关系式为：___ _____，自变量x的取值范围
是：____________；药物燃烧后y关于x的函数关系式为：___________；
（2）研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消 毒开始，至少需要经过几分钟后，学生才能回到教室；
（3）研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效地杀灭空气中的病菌，那么此次消毒是否有效？为什么？点拨拓展3、某单位计划在长和宽分别
为20米和11米的矩形大厅内
修建一个60平方米的矩形健
身房ABCD. 该健身房的四面
墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁
的费用为20元/平方米，新建（含装修）墙壁的费用为80元/平方米. 设健身
房的高为3米，一面旧墙壁AB的长为x米，修建健身房的总投入为y元.
（1）求y与x的函数关系式；
（2）为了合理利用大厅，要求自变量x必须满足8≤x≤12. 当投入资金为4800元时，问利用旧墙壁的总长度为多少米？点拨拓展4、如图已知一次函数y=kx+b（k≠0）的图象与x轴，
y轴分别交于A、B两点，且与反比例函数y=
（m≠0）的图象交于点C，过点C作CD垂直于x轴，
垂足为D，若OA=OB=OD=1.
（1）求点A、B、D的坐标；
（2）求一次函数和反比例函数的解析式点拨拓展