5.2 菱形(1)

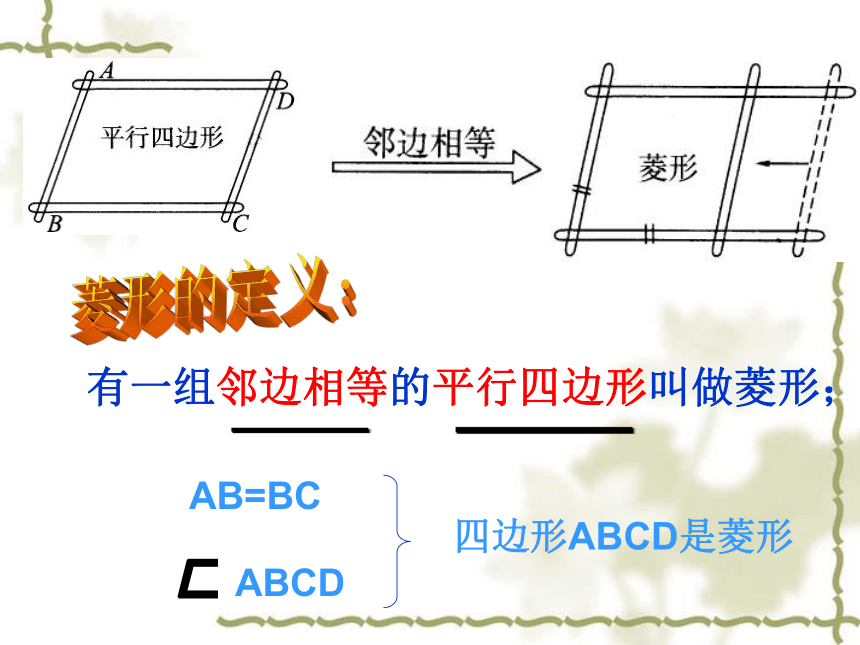
课件28张PPT。新浙教版数学八年级（下）5.2 菱形(1)下面图形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.图片欣赏有一组邻边相等的平行四边形叫做菱形；菱形的定义：AB=BC ABCD四边形ABCD是菱形 由于平行四边形的对边相等，
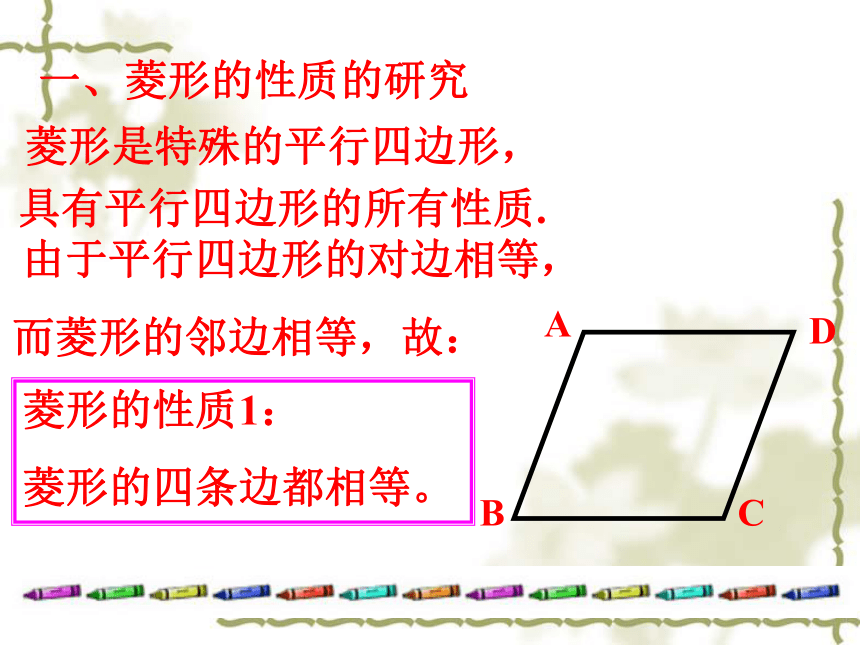
而菱形的邻边相等，故：菱形的性质1：
菱形的四条边都相等。 菱形是特殊的平行四边形，
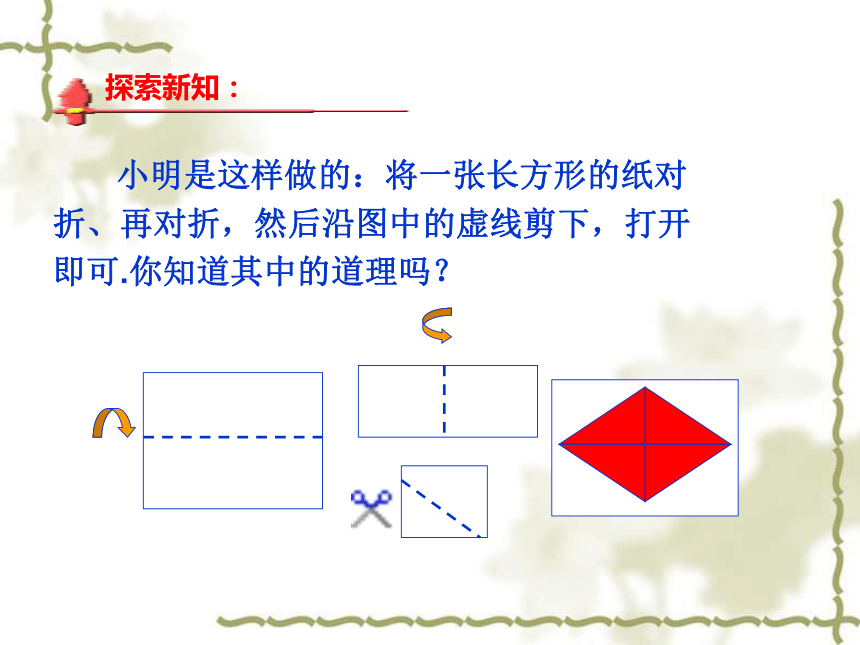
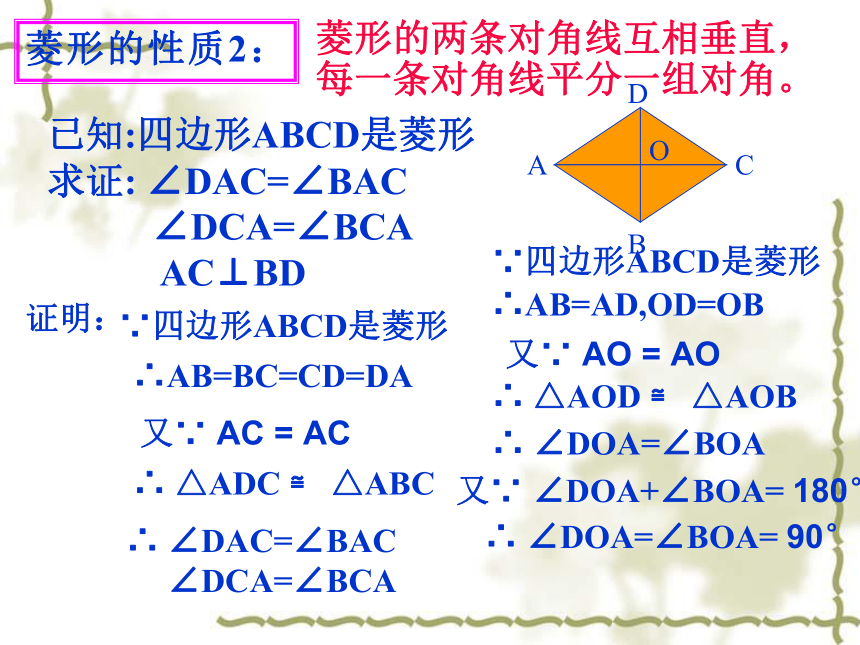
具有平行四边形的所有性质.一、菱形的性质的研究探索新知： （1）菱形是轴对称图形吗？如果是，那么它有几条对称轴？对称轴之间有什么位置关系？ （2）如何利用折纸、剪切的方法，既快又准确地剪出一个菱形的纸片？ 小明是这样做的：将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可.你知道其中的道理吗？探索新知：菱形的两条对角线互相垂直，每一条对角线平分一组对角。∵四边形ABCD是菱形∴AB=BC=CD=DA∴ ∠DAC=∠BAC
∠DCA=∠BCA 又∵ AC = AC∴ △ADC ≌ △ABC∵四边形ABCD是菱形∴AB=AD,OD=OB又∵ AO = AO∴ △AOD ≌ △AOB∴ ∠DOA=∠BOA又∵ ∠DOA+∠BOA= 180°∴ ∠DOA=∠BOA= 90°已知:四边形ABCD是菱形
求证: ∠DAC=∠BAC
∠DCA=∠BCA
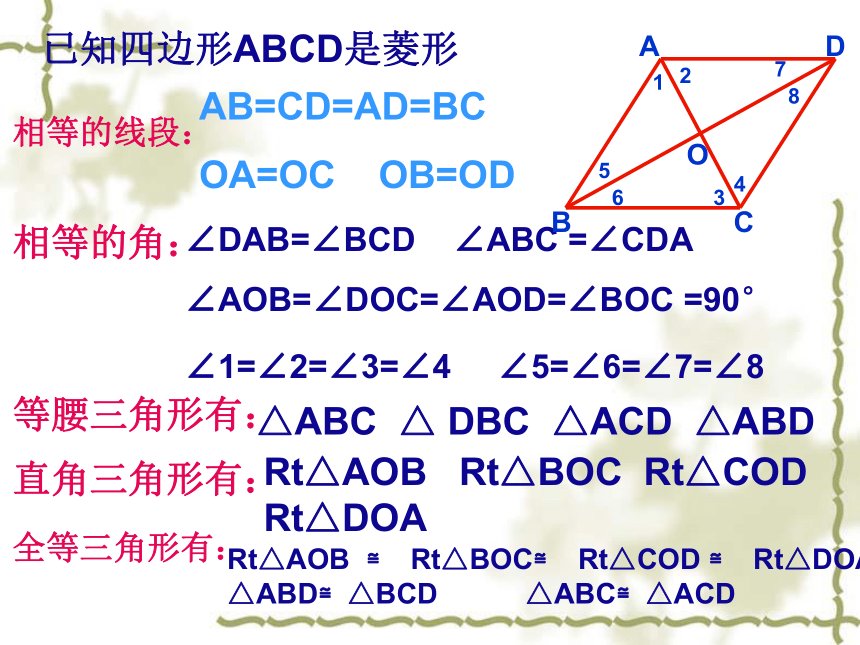
AC⊥BD 菱形的性质2：证明：相等的线段：相等的角：等腰三角形有：直角三角形有：全等三角形有：已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678初步尝试例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.

解:∵四边形ABCD是菱形,
∴AB=CD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
∵∠BAC=30°
∴∠BAD=60°又∵OB=OD=3(平行四边形的对角线互相平分)
AC⊥BD(菱形的对角线互相垂直)
由勾股定理,得AO=
AC=2AO=∴ABD是等边三角形.
AB=BD=6C菱形面积公式的探索OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 面积：S菱形=底×高=对角线乘积的一半O解：∵ 花坛ABCD是菱形 ∴ AC⊥BD, ∠ABO = ∠ABC = ×60°=30° AB = BC = CD = AD = ×80 = 20 (m)在Rt△OAB中，AO= AB= ×20=10(m)BO= ≈17.32（m）∴ 花坛的两条小路长
AC = 2AO = 20 (m)
BD = 2BO ≈34.64(m) 花坛的面积 = AC·BD≈346.4 ( )想一想 矩形、菱形是不是轴对称图形？如果是轴对称图形，对称轴各几条矩形是轴对称图形，对称轴有两条。菱形是轴对称图形，对称轴有两条。对边平行四条边都相等中心对称图形轴对称图形对角相等对角线互相垂直对角线互相平分每一条对角线平分一组对角2、 （a，b表示两条对角线的长度）用列表形式小结出菱形的性质归纳小结,提炼知识1、底乘以高当堂巩固打好基础：比一比，看谁的反应最快！１、下列说法中错误的是（　　）
A、一组邻边相等的平行四边形是菱形；
B、对角线互相垂直的平行四边形是菱形；
C、对角线互相平分的四边形是菱形；
D、菱形的每一条对角线平分一组对角。2、对于以下图形（1）矩形（2）等边三角形（3）平行四边形（4）菱形（5）圆（6）线段， 既是轴对称图形又是中心对称图形的有（ ）
A、1个 B、2个 C、3个 D、4个3、已知菱形的两条对角线长分别是10和24,则
菱形的周长为_____。52CD1.已知菱形的周长是12cm，那么它的边长是______.2.菱形ABCD中∠ABC＝60度，则∠BAC＝_______.3cm60度3.菱形ABCD中,O是两条对角线的交点，已知AB＝5cm,AO=4cm，求两对角线AC、BD的长。4.菱形ABCD中两条对角线的长分别是6cm和8cm,求菱形的周长和面积.巩固新知 例：如图，菱形ABCD的边长为4cm，∠BAD＝1200。对角线AC、BD相交于点O，求这个菱形的对角线长和面积。。解：∵ ∠BAD＝1200 如图，在一种可伸缩的衣帽架中，每个菱形的周长都为100厘米，固定在墙上的两点A、B之间的距离为25厘米，则∠ACB= .ABC菱形ABCD的周长为16，相邻两角的度数比为1：2．⑴求菱形ABCD的对角线的长；⑵求菱形ABCD的面积．菱形的 两条对角线互相平分菱形的两组对边平行且相等边对角线角菱形的性质菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补菱形的两条对角线互相垂直平分，每一条对角线平分一组对角。自我挑战（2）已知：菱形ABCD中，对角线AC与BD相交于点O，且 AC=12，BD=16，则菱形ABCD的面积为 ，边长为 ，周长为 。（1）在菱形ABCD中，∠BAD=2∠B，则∠B= , △ABC是 三角形，∠ABD的度数为________ 。等边30 °96104060 °（3）在菱形ABCD中∠BAC=30°，BD=6㎝，则 ∠BAD= ,∠ABD= ,AB= . 60 °60 °6㎝1、已知,在菱形ABCD中,∠BAD= ,现将一块含 角的三角尺AMN(其中∠NAM= )叠放在菱形上,然后将三角尺绕点A旋转.在旋转过程中,设AM交边BC于点E,AN交边CD于点F,那么BE+DF与AB有着怎样的数量关系?请你通过动手操作、度量、猜想、验证等方法予以探索。挑战自我2、已知如图，菱形ABCD中，E是AB的中点，且DE⊥AB，AE=2。
求（1）∠ABC的度数；
（2）对角线AC、BD的长；
（3）菱形ABCD的面积。2∵四边形ABCD是菱形， ∴AD=AB解：∴AD=AB=BD∵ E是AB的中点，且DE⊥AB
∴DA=DB（DE为AB 的中垂线）∴ ∠DAB= 60 °， ∴ ∠ABC=120 °（2）∵AE=2， ∴ AB=4 ∴ BD=AB=4∵四边形ABCD是菱形，∴ AC⊥DB
∵ DB=4 ∴ 0B=2
∴ 在R t△AOB中,由勾股定理得 2AO=∴ AC=4（3）在Rt△DAE中,由勾股定理得 DE==2∴ S菱形ABCD=4×2=8（1）你对这一步
有什么看法？谢谢大家！