4.4 平行四边形的判定定理(1) 课件(共21张PPT)
文档属性
| 名称 | 4.4 平行四边形的判定定理(1) 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 305.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 21:55:43 | ||
图片预览





文档简介
(共21张PPT)
浙教版八下数学
4.4 平行四边形的判定定理 (1)
教的关键是“听”,学的关键是“说”
作一个两组对边分别相等的四边形.
步骤:
4.顺次连结各点,即得两组对边分别相等的四边形ABCD.
·
·
·
·
A
C
B
D
1.任取两点B、D;
2.分别以点B和点D为圆心、任意长为半径,分别
在线段BD的两侧画弧;
3.再分别以点B和点D为圆心、适当长为半径画弧,与前面所画的弧分别交于点A和点C;
分享你的猜想:
大声说出来
猜想:两组对边分别相等的四边形是平行四边形.
温故知新:
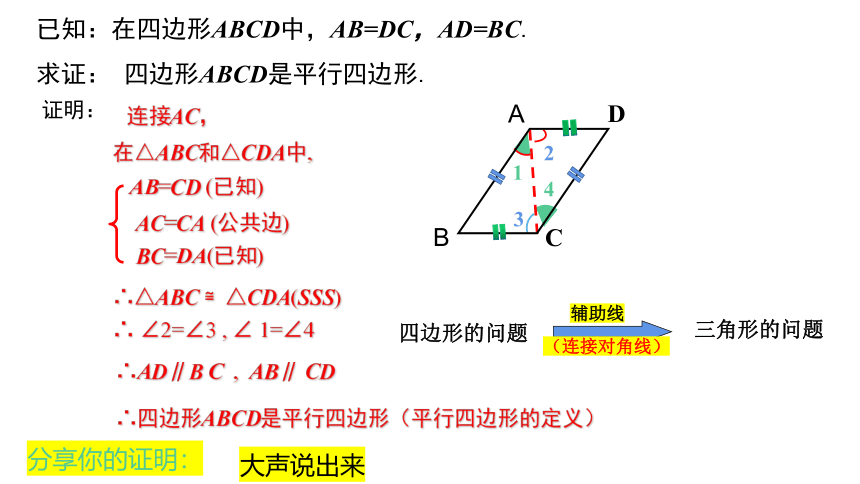
已知:在四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
连接AC,
在△ABC和△CDA中,
AB=CD (已知)
BC=DA(已知)
AC=CA (公共边)
∴△ABC ≌△CDA(SSS)
∴ ∠2=∠3 , ∠ 1=∠4
∴AD∥B C , AB∥ CD
∴四边形ABCD是平行四边形(平行四边形的定义)
证明:
1
4
2
3
A
B
C
D
分享你的证明:
大声说出来
四边形的问题
辅助线
(连接对角线)
三角形的问题
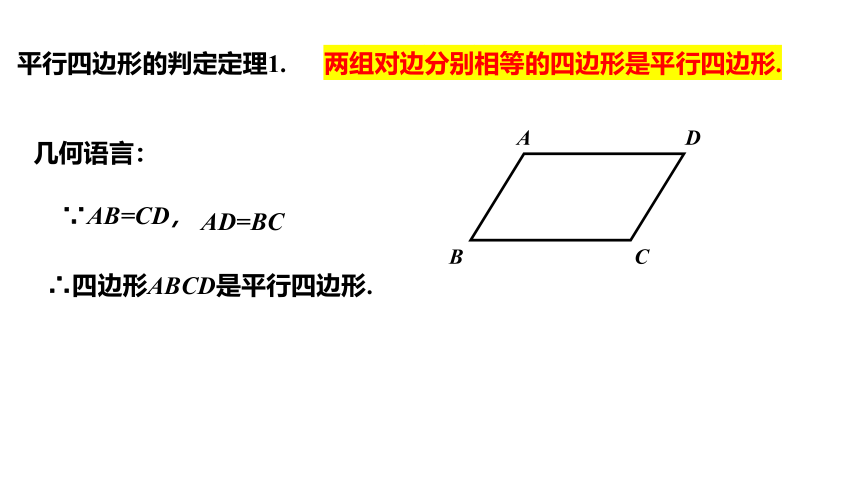
平行四边形的判定定理1. 两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC
∴四边形ABCD是平行四边形.
几何语言:
B
D
C
A
作一个有一组对边平行且相等的四边形.
步骤:
1.任意画两条平行线m、n;
2.在直线m、n上分别截取AB、CD,使AB=CD;
3.分别连结点B、C和点A、D,即得到一组对边平行且相等的四边形ABCD.
m
n
·
·
C
D
·
A
·
B
分享你的猜想:
大声说出来
猜想:一组对边平行且相等的四边形是平行四边形
A
B
C
D
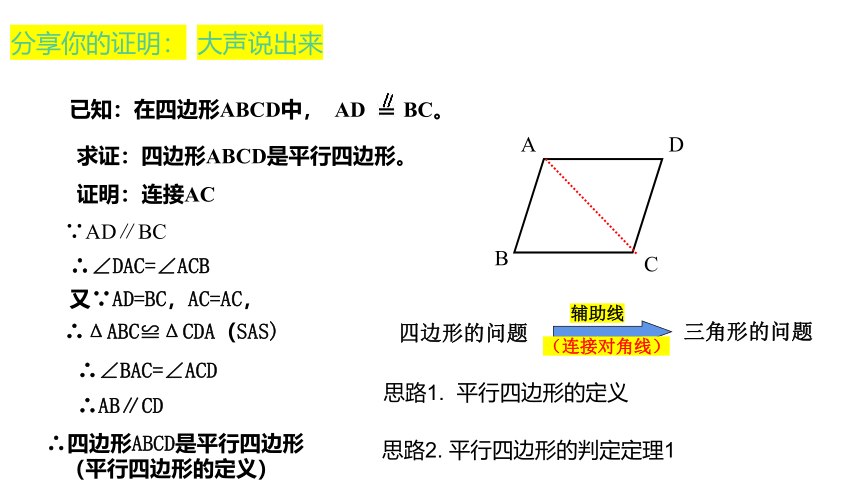
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA(SAS)
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(平行四边形的定义)
已知:在四边形ABCD中, AD BC。
分享你的证明:
大声说出来
四边形的问题
辅助线
(连接对角线)
三角形的问题
思路1. 平行四边形的定义
思路2. 平行四边形的判定定理1
平行四边形的判定定理2. 一组对边平行且相等的四边形是平行四边形.
∴四边形ABCD是平行四边形.
几何语言:
B
D
C
A
∵AB CD,
∥
=
“平行且相等”常用符号“ ”来表示.如图,AB=CD且AB∥CD,可以记作“AB CD”,读作“AB 平行且等于CD”
∥
=
∥
=
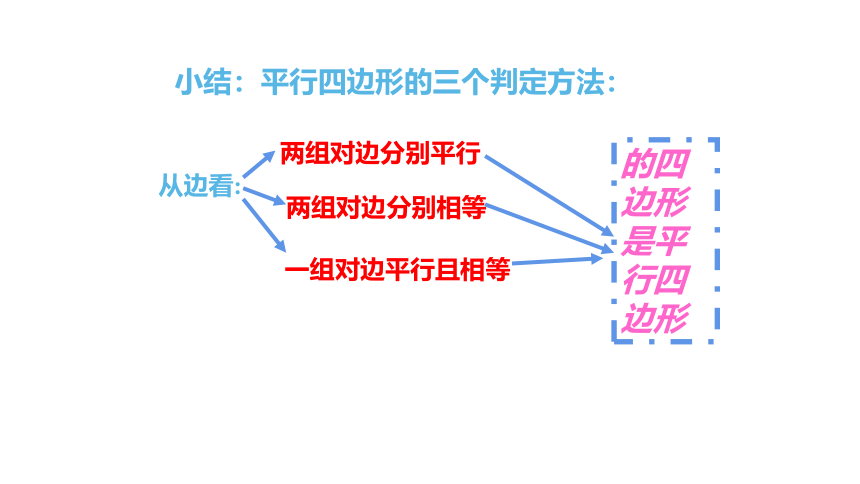
小结:平行四边形的三个判定方法:
从边看:
两组对边分别平行
两组对边分别相等
一组对边平行且相等
的四边形是平行四边形
已知:如图,在 □ABCD 中,E,F分别是AB,CD的中点。
求证:EF∥AD
∵E、F分别为AB、CD的中点
∴AE DF
∴EF ∥AD
∴四边形AEFD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
分享你的证明:
大声说出来
AB DC
证明:在□ABCD 中,
学以致用:
平行四边形的判定:
两组对边
分别平行
一组对边
平行且相等
两组对边
分别相等
平行四边形
对边平行且相等
对角相等
对角线互相平分
平行四边形的性质
知识结构
1、∵AB ∥ CD
__ ∥ __
∴四边形ABCD是平行四边形
( )
2、 ∵AB=CD
__∥__
∴四边形ABCD是平行四边形。
( )
3、∵AB=CD
__=__
∴四边形ABCD是平行四边形
( )
平行四边形的定义
AB CD
AD BC
AD BC
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
当堂检测: 夯实基础,稳扎稳打
B
D
C
A
一、填空(齐声朗读)
2.如图,把线段AB平移到线段A'B',AB与A'B'平行吗?请说明理由
解:AB与A'B'平行
理由如下:
连接AA'、BB'
∵AA' BB',
∴四边形ABCD是平行四边形(一组对边平行并且相等的四边形是平行四边形)
∴AB∥A'B'(平行四边形对边平行)
一个图形沿某个方向移动,在移动过程中,原图形上所有的点都沿同一个方向移动相等的距离,这样的图形运动叫做图形的平移
平行
相等
分享你的证明:
大声说出来
3.已知:如图,AD⊥AC,BC⊥AC,且AB=CD.求证:AB∥CD.
D
C
A
B
证明:
∵AD⊥AC, BC⊥AC,
∴∠BCA=∠DAC=90O,
又∵AB=CD, AC=CA,
∴Rt⊿ACB≌Rt⊿CAD(HL).
∴四边形ABCD是平行四边形
∴AB∥CD(平行四边形的定义)
∴AD=BC,
∴AD∥BC,
分享你的证明:
大声说出来
思路1:三线八角
思路2:平行四边形
4.已知:如图,E,F分别是 ABCD的边AD,BC的中点。
求证:BE=DF.
证明:
∵四边形ABCD是平行四边形,
∴AD ∥BC (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED BF.
∥
﹦
∴四边形EBFD是平行四边形
∴BE=DF(平行四边形的对边分别相等)。
F
E
C
B
A
D
分享你的证明:
大声说出来
思路1:全等出等边
思路2:平行四边形
5.下列命题是真命题还是假命题?如果是假命题,请给出反例。如果是真命题,请给出证明。
(1)一组对边平行,另一组对边相等的四边形是平行四边形。
假命题
等腰梯形
(2)两组邻边相等的四边形是平行四边形。
假命题
筝形
新知讲解
6.已知:四边形ABCD, ∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
同理可证AB∥CD.
又∵∠A+ ∠B+ ∠C+ ∠D =360 °,
∴ 2∠A+ 2∠B=360 °,
∵∠A=∠C,∠B=∠D(已知),
即∠A+ ∠B=180 °.
∴ AD∥BC (同旁内角互补,两直线平行).
A
B
C
D
分享你的证明:
大声说出来
新知归纳
两组对角分别相等的四边形是平行四边形.
平行四边形的判定定理3:
符号语言:
A
B
C
D
∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
(两组对角分别相等的四边形是平行四边形)
A
B
C
D
判定一个四边形是平行边形可以从哪些角度思考 具体有哪些方法
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理)
一组对边平行且相等的四边形是平行四边形(判定定理)
从角考虑
两组对角分别相等的四边形是平行四边形(判定定理)
A
B
C
D
E
F
7.已知:如图,在等边三角形ABC中,D、E、F分别为各边的中点。
求证:四边形DEFB是平行四边形
分享你的证明:
大声说出来
证明:∵ΔABC等边三角形
∵∠EDC=∠B=600
∴ΔAEF, ΔCDE 都是等边三角形
D、E、F分别为各边的中点
∴∠AFE=∠B=600
∴ EF∥BD
∴ ED∥FB
∴ 四边形DEFB是平行四边形
连续递推,豁然开朗
A
B
C
D
E
8.已知:如图,在梯形ABCD中,CD∥AB,AD=BC,
E是AB上一点, 且AE=CD,∠B=600,
求证:ΔEBC是等边三角形
∴ΔEBC是等边三角形
证明:∵CD∥AB,AE=CD
∴四边形ABCD是平行四边形
∴AD=CE
∵AD=BC
∴CE=BC
∵∠B=600
分享你的证明:
大声说出来
A
B
C
D
E
F
9.已知:如图,E,F分别是 ABCD的对角线AC上的两点,且AE=CF
求证:四边形BFDE是平行四边形
分享你的证明:
大声说出来
思路1:
两组对边分别相等的四边形是平行四边形
思路2:
一组对边且相等的四边形是平行四边形
思路3:
两组对边分别平行的四边形是平行四边形
A
B
C
D
E
F
备用图1.
备用图2.
浙教版八下数学
4.4 平行四边形的判定定理 (1)
教的关键是“听”,学的关键是“说”
作一个两组对边分别相等的四边形.
步骤:
4.顺次连结各点,即得两组对边分别相等的四边形ABCD.
·
·
·
·
A
C
B
D
1.任取两点B、D;
2.分别以点B和点D为圆心、任意长为半径,分别
在线段BD的两侧画弧;
3.再分别以点B和点D为圆心、适当长为半径画弧,与前面所画的弧分别交于点A和点C;
分享你的猜想:
大声说出来
猜想:两组对边分别相等的四边形是平行四边形.
温故知新:
已知:在四边形ABCD中,AB=DC,AD=BC.
求证: 四边形ABCD是平行四边形.
连接AC,
在△ABC和△CDA中,
AB=CD (已知)
BC=DA(已知)
AC=CA (公共边)
∴△ABC ≌△CDA(SSS)
∴ ∠2=∠3 , ∠ 1=∠4
∴AD∥B C , AB∥ CD
∴四边形ABCD是平行四边形(平行四边形的定义)
证明:
1
4
2
3
A
B
C
D
分享你的证明:
大声说出来
四边形的问题
辅助线
(连接对角线)
三角形的问题
平行四边形的判定定理1. 两组对边分别相等的四边形是平行四边形.
∵AB=CD,
AD=BC
∴四边形ABCD是平行四边形.
几何语言:
B
D
C
A
作一个有一组对边平行且相等的四边形.
步骤:
1.任意画两条平行线m、n;
2.在直线m、n上分别截取AB、CD,使AB=CD;
3.分别连结点B、C和点A、D,即得到一组对边平行且相等的四边形ABCD.
m
n
·
·
C
D
·
A
·
B
分享你的猜想:
大声说出来
猜想:一组对边平行且相等的四边形是平行四边形
A
B
C
D
求证:四边形ABCD是平行四边形。
证明:连接AC
∵AD∥BC
∴∠DAC=∠ACB
又∵AD=BC,AC=AC,
∴ΔABC≌ΔCDA(SAS)
∴∠BAC=∠ACD
∴AB∥CD
∴四边形ABCD是平行四边形
(平行四边形的定义)
已知:在四边形ABCD中, AD BC。
分享你的证明:
大声说出来
四边形的问题
辅助线
(连接对角线)
三角形的问题
思路1. 平行四边形的定义
思路2. 平行四边形的判定定理1
平行四边形的判定定理2. 一组对边平行且相等的四边形是平行四边形.
∴四边形ABCD是平行四边形.
几何语言:
B
D
C
A
∵AB CD,
∥
=
“平行且相等”常用符号“ ”来表示.如图,AB=CD且AB∥CD,可以记作“AB CD”,读作“AB 平行且等于CD”
∥
=
∥
=
小结:平行四边形的三个判定方法:
从边看:
两组对边分别平行
两组对边分别相等
一组对边平行且相等
的四边形是平行四边形
已知:如图,在 □ABCD 中,E,F分别是AB,CD的中点。
求证:EF∥AD
∵E、F分别为AB、CD的中点
∴AE DF
∴EF ∥AD
∴四边形AEFD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
分享你的证明:
大声说出来
AB DC
证明:在□ABCD 中,
学以致用:
平行四边形的判定:
两组对边
分别平行
一组对边
平行且相等
两组对边
分别相等
平行四边形
对边平行且相等
对角相等
对角线互相平分
平行四边形的性质
知识结构
1、∵AB ∥ CD
__ ∥ __
∴四边形ABCD是平行四边形
( )
2、 ∵AB=CD
__∥__
∴四边形ABCD是平行四边形。
( )
3、∵AB=CD
__=__
∴四边形ABCD是平行四边形
( )
平行四边形的定义
AB CD
AD BC
AD BC
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
当堂检测: 夯实基础,稳扎稳打
B
D
C
A
一、填空(齐声朗读)
2.如图,把线段AB平移到线段A'B',AB与A'B'平行吗?请说明理由
解:AB与A'B'平行
理由如下:
连接AA'、BB'
∵AA' BB',
∴四边形ABCD是平行四边形(一组对边平行并且相等的四边形是平行四边形)
∴AB∥A'B'(平行四边形对边平行)
一个图形沿某个方向移动,在移动过程中,原图形上所有的点都沿同一个方向移动相等的距离,这样的图形运动叫做图形的平移
平行
相等
分享你的证明:
大声说出来
3.已知:如图,AD⊥AC,BC⊥AC,且AB=CD.求证:AB∥CD.
D
C
A
B
证明:
∵AD⊥AC, BC⊥AC,
∴∠BCA=∠DAC=90O,
又∵AB=CD, AC=CA,
∴Rt⊿ACB≌Rt⊿CAD(HL).
∴四边形ABCD是平行四边形
∴AB∥CD(平行四边形的定义)
∴AD=BC,
∴AD∥BC,
分享你的证明:
大声说出来
思路1:三线八角
思路2:平行四边形
4.已知:如图,E,F分别是 ABCD的边AD,BC的中点。
求证:BE=DF.
证明:
∵四边形ABCD是平行四边形,
∴AD ∥BC (平行四边形的定义)
AD=BC(平行四边形的对边分别相等),
∵E,F分别是AD,BC的中点,
∴ED=BF,即ED BF.
∥
﹦
∴四边形EBFD是平行四边形
∴BE=DF(平行四边形的对边分别相等)。
F
E
C
B
A
D
分享你的证明:
大声说出来
思路1:全等出等边
思路2:平行四边形
5.下列命题是真命题还是假命题?如果是假命题,请给出反例。如果是真命题,请给出证明。
(1)一组对边平行,另一组对边相等的四边形是平行四边形。
假命题
等腰梯形
(2)两组邻边相等的四边形是平行四边形。
假命题
筝形
新知讲解
6.已知:四边形ABCD, ∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
证明:
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
同理可证AB∥CD.
又∵∠A+ ∠B+ ∠C+ ∠D =360 °,
∴ 2∠A+ 2∠B=360 °,
∵∠A=∠C,∠B=∠D(已知),
即∠A+ ∠B=180 °.
∴ AD∥BC (同旁内角互补,两直线平行).
A
B
C
D
分享你的证明:
大声说出来
新知归纳
两组对角分别相等的四边形是平行四边形.
平行四边形的判定定理3:
符号语言:
A
B
C
D
∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
(两组对角分别相等的四边形是平行四边形)
A
B
C
D
判定一个四边形是平行边形可以从哪些角度思考 具体有哪些方法
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理)
一组对边平行且相等的四边形是平行四边形(判定定理)
从角考虑
两组对角分别相等的四边形是平行四边形(判定定理)
A
B
C
D
E
F
7.已知:如图,在等边三角形ABC中,D、E、F分别为各边的中点。
求证:四边形DEFB是平行四边形
分享你的证明:
大声说出来
证明:∵ΔABC等边三角形
∵∠EDC=∠B=600
∴ΔAEF, ΔCDE 都是等边三角形
D、E、F分别为各边的中点
∴∠AFE=∠B=600
∴ EF∥BD
∴ ED∥FB
∴ 四边形DEFB是平行四边形
连续递推,豁然开朗
A
B
C
D
E
8.已知:如图,在梯形ABCD中,CD∥AB,AD=BC,
E是AB上一点, 且AE=CD,∠B=600,
求证:ΔEBC是等边三角形
∴ΔEBC是等边三角形
证明:∵CD∥AB,AE=CD
∴四边形ABCD是平行四边形
∴AD=CE
∵AD=BC
∴CE=BC
∵∠B=600
分享你的证明:
大声说出来
A
B
C
D
E
F
9.已知:如图,E,F分别是 ABCD的对角线AC上的两点,且AE=CF
求证:四边形BFDE是平行四边形
分享你的证明:
大声说出来
思路1:
两组对边分别相等的四边形是平行四边形
思路2:
一组对边且相等的四边形是平行四边形
思路3:
两组对边分别平行的四边形是平行四边形
A
B
C
D
E
F
备用图1.
备用图2.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
