2.5 有理数的乘方(第1课时)课件

课件24张PPT。第二章 有理数的运算§2.5 有理数的乘方
（第1课时）课前 · 预学区本课目标预习填空基础自测温故知新自主学习　基础落实 1. 理解乘方、幂、指数、底数的概念．
2. 掌握乘方和幂的表示法．
3. 学会判定幂的符号，并会进行简单有理数乘方
的运算．
4. 会进行乘方、乘、除的简单混合运算．课前 · 预学区自主学习　基础落实 本课目标预习填空基础自测温故知新 求两个相同因数的积的运算叫做平方，求三个相同
因数的积的运算叫做立方．
3×3可以写成_____，3×3×3，可以写成_____，
依此类推，an(n为正整数)表示____个____的乘积．3233na课前 · 预学区自主学习　基础落实 本课目标预习填空基础自测温故知新2. 若干个不为零的数相乘时，结果的符号由负因数的
个数决定．
若干个不为零的数相乘时，当负因数的个数是偶
数个时，则积的符号是________，当负因数的个
数是奇数个时，则积的符号是________．　负 正课前 · 预学区自主学习　基础落实 本课目标预习填空基础自测温故知新 求几个相同因数的积的运算叫做________，其中相
同的因数叫做________．
2. (－3)4表示__________相乘，指数是__________，底数是__________．－3乘方底数4个－34课前 · 预学区自主学习　基础落实 本课目标预习填空基础自测温故知新 －63表示的意义是____________________， 它与
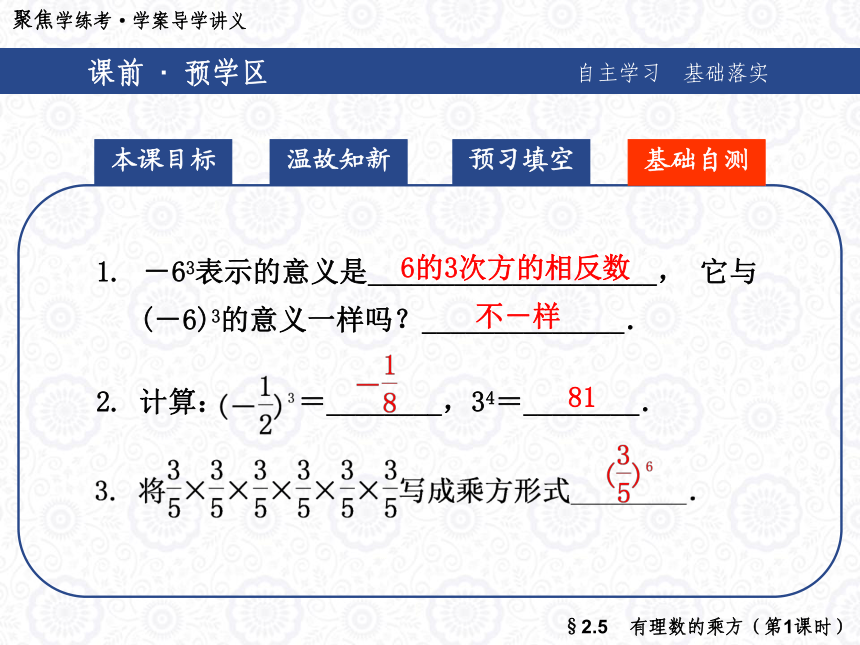
(－6)3的意义一样吗？______________．　不－样 6的3次方的相反数2. 计算： ＝________，34＝________．81 典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例1】　计算(－3)4和－34的值．典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例1】　计算(－3)4和－34的值．要理解(－3)4和－34的差异，比较两者
的底数和结果，并进行归纳．典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例1】　计算(－3)4和－34的值．解：(－3)4
＝(－3)×(－3)×(－3)×(－3)
＝81；
－34
＝－3×3×3×3
＝81.典例 · 精析区以题说法　互动探究变式训练1　 (2)求(－1)12和－112的值．解：(－1)12＝1，－112＝－1.典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例2】 计算：
(1)(5×2)3 (2)(－5)3×(－2)3
(3)(－2)3÷(－22)典例 · 精析区以题说法　互动探究关键在于弄请楚乘方与乘除混合运算的
运算顺序．答 案点 拨变式训练【例2】 计算：
(1)(5×2)3 (2)(－5)3×(－2)3
(3)(－2)3÷(－22)典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例2】 计算：
(1)(5×2)3 (2)(－5)3×(－2)3
(3)(－2)3÷(－22)解：(1)原式＝103＝10×10×10＝1000　
(2)原式＝(－5)×(－5)×(－5)×(－2)
×(－2)×(－2)
＝(5×2)×(5×2)×(5×2)
＝10×10×10＝1000　
(3)原式＝(－2)×(－2)×(－2)÷(－2×2)
＝－8÷(－4)
＝2典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例2】 计算：
(1)(5×2)3 (2)(－5)3×(－2)3
(3)(－2)3÷(－22)2. 计算：
(1)(－6÷2)3
(2)(－5)2×(－3)3
(3)(－42)÷(－2)3=2 =－27=－675归纳总结1. 乘方是一种新运算，是一种特殊的乘法运算．
2. 乘方运算通常要转化成乘法来完成，乘方运算与
加减乘除运算一样，要先确定幂的符号，然后再
计算幂的绝对值．
3. 底数、指数、幂、乘方这些概念是很容易混淆的，
要分清；要分清(－a)b与－ab的区别．
4. 对于乘除和乘方的混合运算，应先算乘方，后算
乘除；如果遇到括号，就先进行括号里的运算．随堂 · 检测区即时演练　查漏补缺 A. 基础部分（共8题，每题10分） (一)选择题
1. 下列各组数中，不相等的是 (　　)　　　　　　　　　　　　　　　
A. (－2)3和－23 B. (－3)2和(＋3)2
C. |－2|3和|－23| D. (－3)2和－32D随堂 · 检测区即时演练　查漏补缺 B随堂 · 检测区即时演练　查漏补缺 3. 下列四个式子，正确的是 (　　)
A. 若a≠b，那么a2≠b2
B. 若|a|>|b|，那么a>b
C. 若a>|b|，那么a2>b2
D. 若a2>b2，那么a>bC随堂 · 检测区即时演练　查漏补缺 4. 计算：(－2)100＋(－2)101的值是 (　　)
A. 2100 B. －1
C. －2 D. －2100D随堂 · 检测区即时演练　查漏补缺 (二)填空题
5. 比较大小：
32 ______23，(－5)2 ______52， 6. 立方等于 的数是_____；平方等于 的数是_____．7. 如果一个数的5次幂是负数，那么这个数的2013次幂
是______数．(填“正”或“负”)　　< >＝负 随堂 · 检测区即时演练　查漏补缺 (三)解答题
8. 计算：
(1)－32×(－2)3(3)1000×(1＋10%)2(4)(－3)3＋(－2)4 原式＝72解：原式＝1210原式＝－11 随堂 · 检测区即时演练　查漏补缺 B. 提高部分（共2题，每题10分） 9. 计算：(－0.125)5×84解：原式＝(－0.125)×(－0.125)×(－0.125)×
(－0.125)×(－0.125)×8×8×8×8
＝(－0.125×8)×(－0.125×8)×(－0.125×8)×
(－0.125×8)×(－0.125)
＝(－1)×(－1)×(－1)×(－1)×(－0.125)
＝－0.125　 随堂 · 检测区即时演练　查漏补缺 10. 观察下列各式，回答下列问题：
0．12＝0.01，0.012＝0.0001，102＝100，1002＝10000.
0．13＝0.001，0.013＝0.000001，103＝1000，1003＝
1000000.
(1)当底数的小数点向左(或向右)移动一位时，其平方数
的小数点向左(或向右)移动几位？
(2)当底数的小数点向左(或向右)移动一位时，其立方数
的小数点向左(或向右)移动几位？
(3)填空(不操作计算器)：已知：
0．1232＝0.015129，则12.32＝____________；
0．1233＝0.001860867，则1233＝____________．18608672位3位151.29随堂 · 检测区即时演练　查漏补缺 C. 头脑风暴（选做题，20分） 11. 如图，是面积为1的正方形，你能利用图形求出
的值吗？