3.3立方根

课件27张PPT。第三章 实 数§3.3 立方根课前 · 预学区本课目标预习填空基础自测温故知新自主学习　基础落实 1. 了解立方根的概念；
2. 会用根号表示一个数的立方根，并能用立方根运算
求某些数的立方根；
3. 在参与数学学习活动中，不断培养合作交流的良好
习惯．课前 · 预学区自主学习　基础落实 本课目标预习填空基础自测温故知新 立方根：一般地，如果一个数x的立方等于a，即x3＝a，
那么这个数x就叫做a的立方根(也叫做a的三次方根)．
2. 立方根的表示法：如果x3＝a，那么x＝ ，其中a是被
开方数，3是根指数．
3. 立方根的特性：正数有一个正的立方根，负数有一个负
的立方根，0的立方根是0.课前 · 预学区自主学习　基础落实 本课目标预习填空基础自测温故知新 立方根的事实：正数的立方根是________，0的立方根
是________，负数的立方根是________．
2. 立方根与平方根的区别与联系是什么？
______________________________________________.
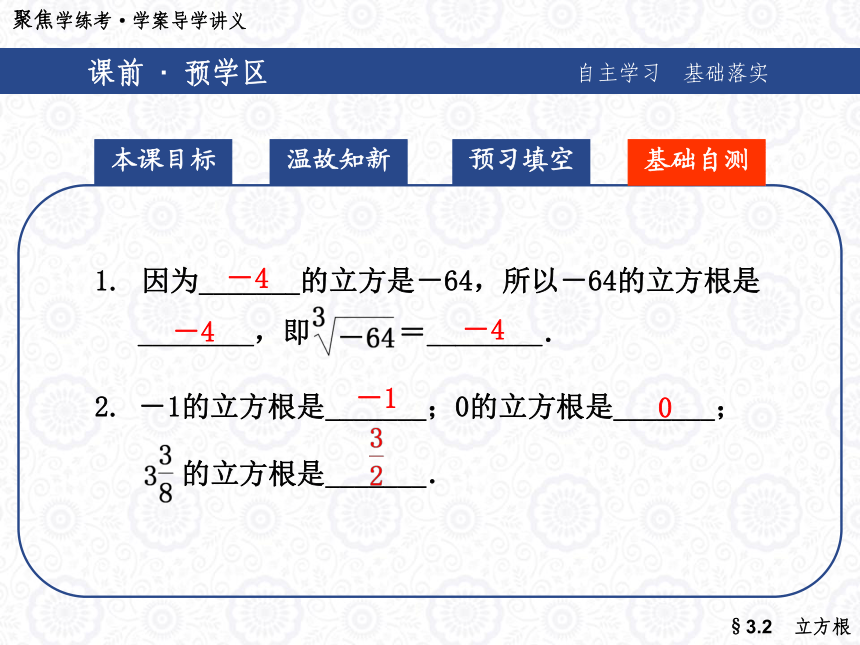
3. 求一个数的立方根的运算叫做________．开立方正数0负数略课前 · 预学区自主学习　基础落实 本课目标预习填空基础自测温故知新 因为_______的立方是－64，所以－64的立方根是
________，即 ＝________．
2. －1的立方根是_______；0的立方根是_______；
的立方根是_______．－4－4－4－10课前 · 预学区自主学习　基础落实 本课目标预习填空基础自测温故知新3. 一个体积为8cm3的正方体，其棱长是_______cm.
4. 一个数的立方根是它本身，则这个数是 (　　)
A. 1 B. 0或1
C. －1或1 D. 1，0或－1D2典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例1】　求下列各数的立方根：典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例1】　求下列各数的立方根：引导学生从一个数的立方入手，确定什么
数的立方等于上述各个结果．
遇有带分数时难以直接确定它的立方根，
常先转化为假分数，再去找它的立方根．典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例1】　求下列各数的立方根：典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例1】　求下列各数的立方根：典例 · 精析区以题说法　互动探究【例1】　求下列各数的立方根：答 案点 拨变式训练1. 求下列各数的立方根：解：(1)0.5 典例 · 精析区以题说法　互动探究答 案点 拨变式训练【例2】 一个正方体木块的体积是125cm3，现将它锯成8块同
样大小的正方体小木块，求每个小正方体木块的表面积．典例 · 精析区以题说法　互动探究答 案点 拨【例2】 一个正方体木块的体积是125cm3，现将它锯成8块同
样大小的正方体小木块，求每个小正方体木块的表面积．引导学生明确一个正方体的棱长实质上可以
理解为它的体积的立方根，再结合正方形面
积为边长的平方进行列式计算，从而解决了
实际问题．变式训练典例 · 精析区以题说法　互动探究答 案点 拨【例2】 一个正方体木块的体积是125cm3，现将它锯成8块同
样大小的正方体小木块，求每个小正方体木块的表面积．变式训练典例 · 精析区以题说法　互动探究【例2】 一个正方体木块的体积是125cm3，现将它锯成8块同
样大小的正方体小木块，求每个小正方体木块的表面积．答 案点 拨2. 一个立方体的体积是27cm3，将它锯成
64个同样大小的小立方体，求每个小
立方体的表面积．变式训练归纳总结1. 回顾理解立方根的概念．
2. 明确立方根的表示．
3. 掌握立方根的事实．
4. 掌握立方根与平方根的区别与联系．随堂 · 检测区即时演练　查漏补缺 A. 基础部分（共8题，每题10分） D随堂 · 检测区即时演练　查漏补缺 D随堂 · 检测区即时演练　查漏补缺 C随堂 · 检测区即时演练　查漏补缺 4. 下列说法中，正确的是 (　　)
A. 一个正数的平方根和立方根都只有一个
B. 零的平方根和立方根是零
C. 1的平方根与立方根都等于它本身
D. 一个数的立方根与其自身相等的数只有－1B随堂 · 检测区即时演练　查漏补缺 －8 3－8　－27 －2随堂 · 检测区即时演练　查漏补缺 原式=4原式=10随堂 · 检测区即时演练　查漏补缺 B. 提高部分（共2题，每题10分） 随堂 · 检测区即时演练　查漏补缺 B. 提高部分（共2题，每题10分） 解析：此题可采用特殊值法．随堂 · 检测区即时演练　查漏补缺 B. 提高部分（共2题，每题10分） A随堂 · 检测区即时演练　查漏补缺 求|a－1|＋|a|＋2a的值．随堂 · 检测区即时演练　查漏补缺 C. 头脑风暴（选做题，20分）