浙教版数学九年级下册 3.4 简单几何体的表面展开图(1)课件(共16张PPT)
文档属性
| 名称 | 浙教版数学九年级下册 3.4 简单几何体的表面展开图(1)课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 462.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 09:59:33 | ||
图片预览


文档简介
(共16张PPT)
3.4简单几何体的表面展开图(第1课时)
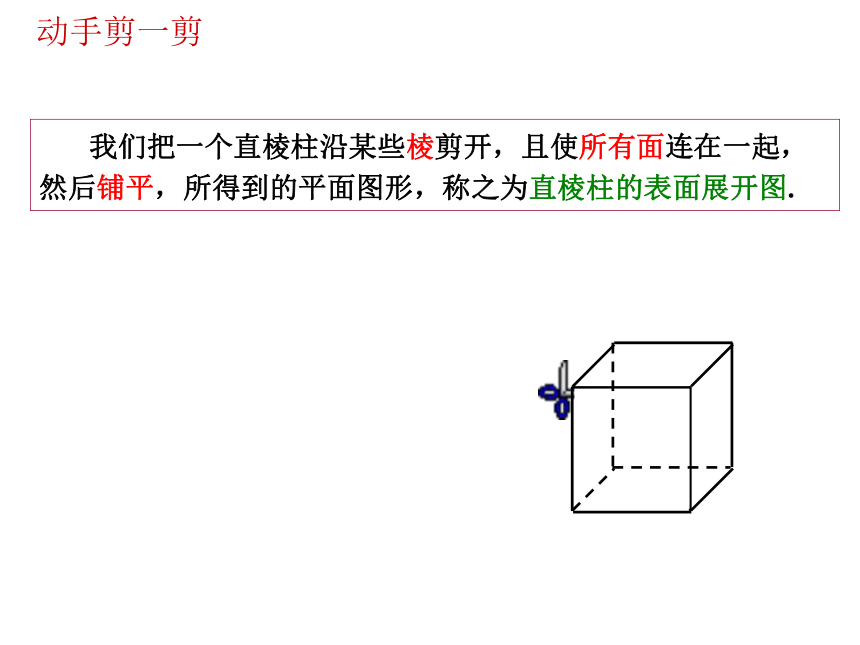
我们把一个直棱柱沿某些棱剪开,且使所有面连在一起,然后铺平,所得到的平面图形,称之为直棱柱的表面展开图.
动手剪一剪
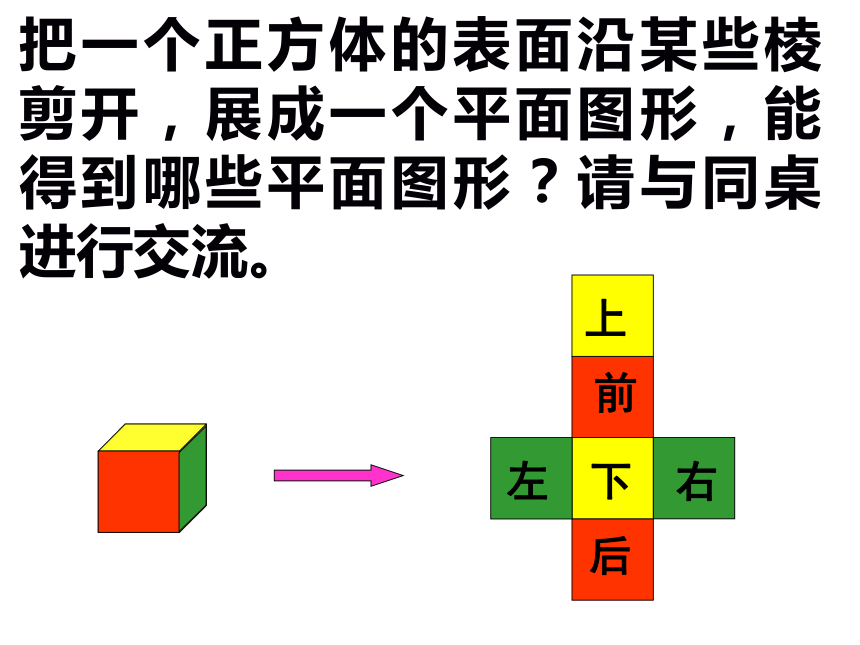
把一个正方体的表面沿某些棱剪开,展成一个平面图形,能得到哪些平面图形?请与同桌进行交流。
上
下
前
后
左
右
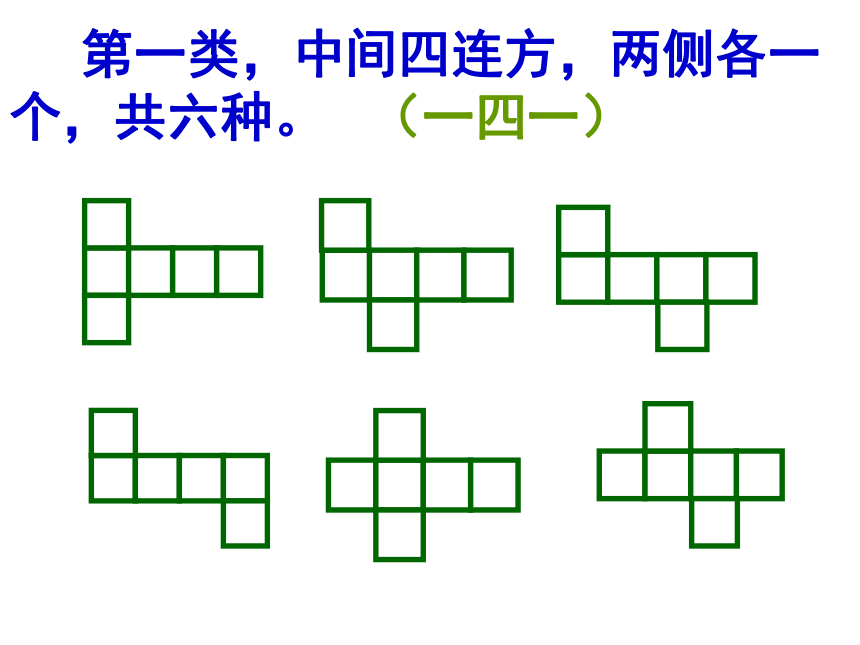
第一类,中间四连方,两侧各一个,共六种。 (一四一)
第二类,中间三连方,两侧各有一、二个,共三种。
(二三一)
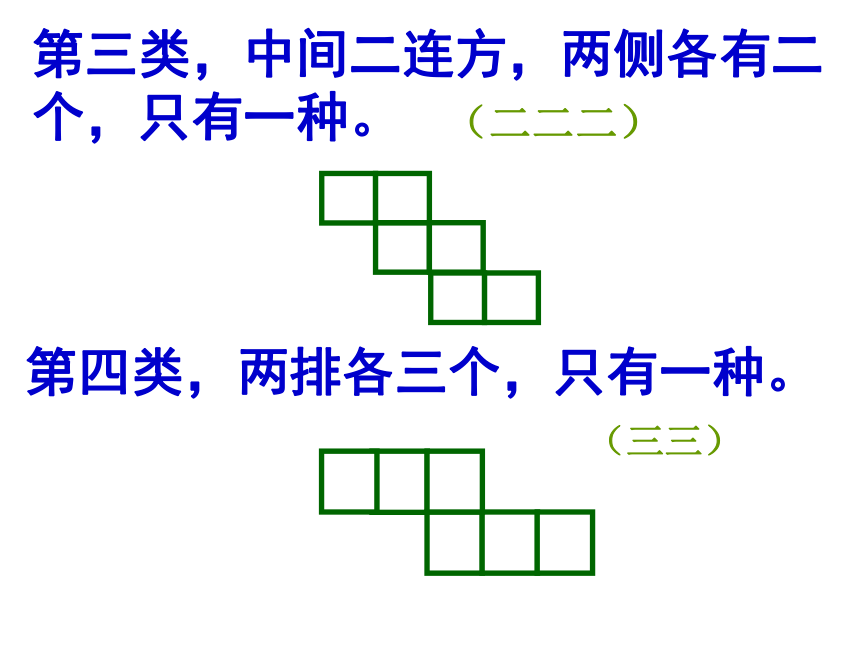
第三类,中间二连方,两侧各有二个,只有一种。
第四类,两排各三个,只有一种。
(二二二)
(三三)
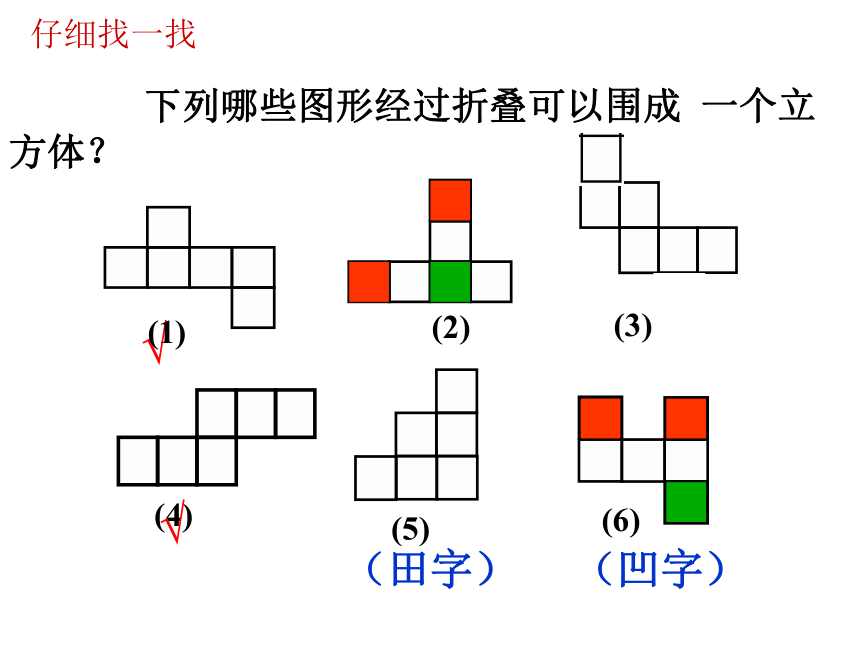
下列哪些图形经过折叠可以围成 一个立方体?
仔细找一找
√
(1)
(2)
(4)
(5)
(6)
(3)
√
(凹字)
(田字)
如图是立方体的表面展开图,要求折成立方体后,使得6在前,右面是3,哪个面在上?左边是几?
动脑想一想
3
6
1
2
4
5
3、如下图是一个正方体的展开图,每个面内部都标注了字母,请根据要求填空:
1)如果D面在左面,那么F面在 ;
2)如果B面在后面,从左面看是D面,那么上面是 。
A
B
F
C
E
D
A
B
C
D
E
F
4、把下图折起来,它会变成正方体( )
A
B
C
D
2、下面的正方体展开后,可能是四个平面图中的哪一个?(先想象,然后动手试试)
A
B
C
D
(甲)
(乙)
(丙)
例2、下列三个平面图形能折叠成牛奶盒吗?
√
√
学以致用
(甲)
b
h
b
b
b
学以致用
例2:有一种牛奶软包装盒如图, 它的长是 cm, 宽是bcm, 高是hcm.求出包装盒的侧面积和表面积.
6cm
B
A处有一只蚂蚁,在B处有一粒蜜糖,蚂蚁想吃到蜜糖,所走的最短路程是多少cm?
B
A
延伸学习
A
B
6cm
4cm
10cm
有一个长宽高分别为6cm、4cm、10cm的长方体牛奶盒,一只蚂蚁在A处,一滴牛奶在B处,试问:蚂蚁去喝牛奶需要爬行的最短路程是多少cm?
延伸学习
A
B
C
6cm
10cm
4cm
E
D
H
F
3.4简单几何体的表面展开图(第1课时)
我们把一个直棱柱沿某些棱剪开,且使所有面连在一起,然后铺平,所得到的平面图形,称之为直棱柱的表面展开图.
动手剪一剪
把一个正方体的表面沿某些棱剪开,展成一个平面图形,能得到哪些平面图形?请与同桌进行交流。
上
下
前
后
左
右
第一类,中间四连方,两侧各一个,共六种。 (一四一)
第二类,中间三连方,两侧各有一、二个,共三种。
(二三一)
第三类,中间二连方,两侧各有二个,只有一种。
第四类,两排各三个,只有一种。
(二二二)
(三三)
下列哪些图形经过折叠可以围成 一个立方体?
仔细找一找
√
(1)
(2)
(4)
(5)
(6)
(3)
√
(凹字)
(田字)
如图是立方体的表面展开图,要求折成立方体后,使得6在前,右面是3,哪个面在上?左边是几?
动脑想一想
3
6
1
2
4
5
3、如下图是一个正方体的展开图,每个面内部都标注了字母,请根据要求填空:
1)如果D面在左面,那么F面在 ;
2)如果B面在后面,从左面看是D面,那么上面是 。
A
B
F
C
E
D
A
B
C
D
E
F
4、把下图折起来,它会变成正方体( )
A
B
C
D
2、下面的正方体展开后,可能是四个平面图中的哪一个?(先想象,然后动手试试)
A
B
C
D
(甲)
(乙)
(丙)
例2、下列三个平面图形能折叠成牛奶盒吗?
√
√
学以致用
(甲)
b
h
b
b
b
学以致用
例2:有一种牛奶软包装盒如图, 它的长是 cm, 宽是bcm, 高是hcm.求出包装盒的侧面积和表面积.
6cm
B
A处有一只蚂蚁,在B处有一粒蜜糖,蚂蚁想吃到蜜糖,所走的最短路程是多少cm?
B
A
延伸学习
A
B
6cm
4cm
10cm
有一个长宽高分别为6cm、4cm、10cm的长方体牛奶盒,一只蚂蚁在A处,一滴牛奶在B处,试问:蚂蚁去喝牛奶需要爬行的最短路程是多少cm?
延伸学习
A
B
C
6cm
10cm
4cm
E
D
H
F
