4.5 三角形的中位线 课件 (共26张PPT)
文档属性
| 名称 | 4.5 三角形的中位线 课件 (共26张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-28 16:21:57 | ||
图片预览



文档简介
(共26张PPT)
4.5 三角形的中位线
浙教版八下数学
新知导入
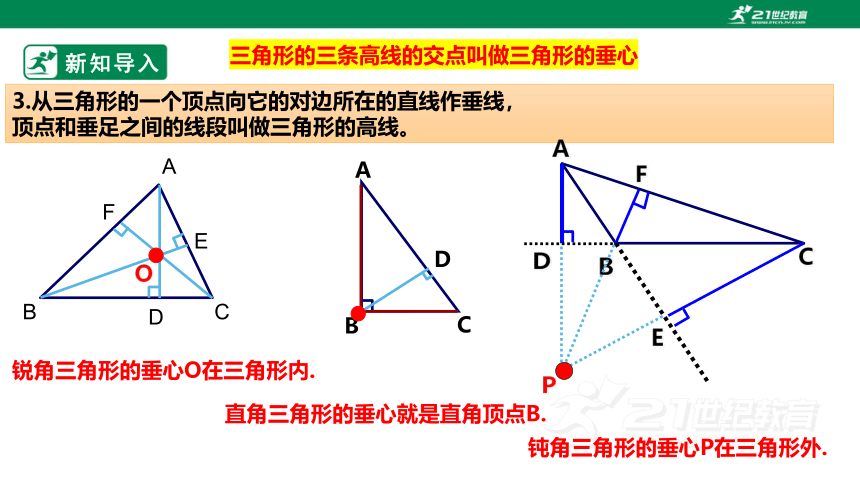
1.在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段, 叫做三角形的角平分线.
A
B
C
D
∵AD是△ABC的角平分线,
∴∠BAD =∠CAD =
∠BAC.
2.在三角形中,连结三角形的一个顶点与该顶点对边中点的线段,叫做这个三角形的中线.
A
D
C
B
∵AD是△ABC的中线,
∴BD=CD= BC
新知导入
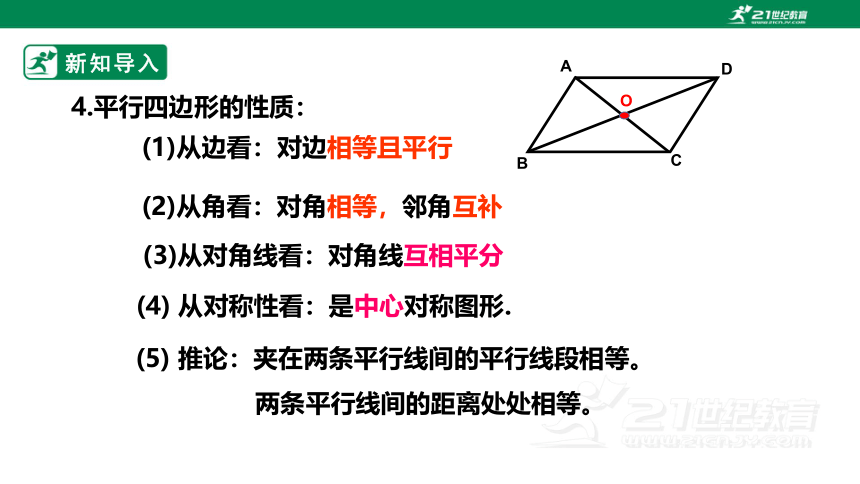
3.从三角形的一个顶点向它的对边所在的直线作垂线,
顶点和垂足之间的线段叫做三角形的高线。
A
B
C
A
B
C
A
B
C
D
E
F
锐角三角形的垂心O在三角形内.
D
直角三角形的垂心就是直角顶点B.
F
D
E
P
钝角三角形的垂心P在三角形外.
三角形的三条高线的交点叫做三角形的垂心
O
新知导入
A
B
C
D
O
4.平行四边形的性质:
(1)从边看:对边相等且平行
(2)从角看:对角相等,邻角互补
(3)从对角线看:对角线互相平分
(4) 从对称性看:是中心对称图形.
(5) 推论:夹在两条平行线间的平行线段相等。
两条平行线间的距离处处相等。
新知导入
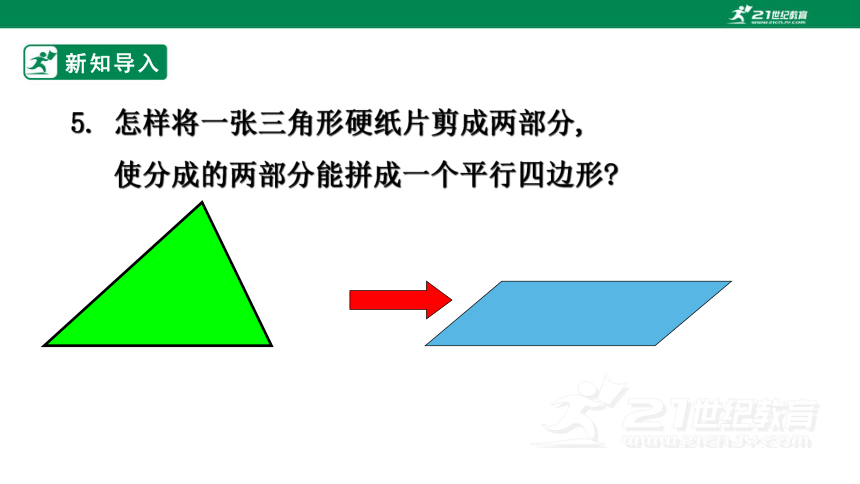
5. 怎样将一张三角形硬纸片剪成两部分,
使分成的两部分能拼成一个平行四边形
新知导入
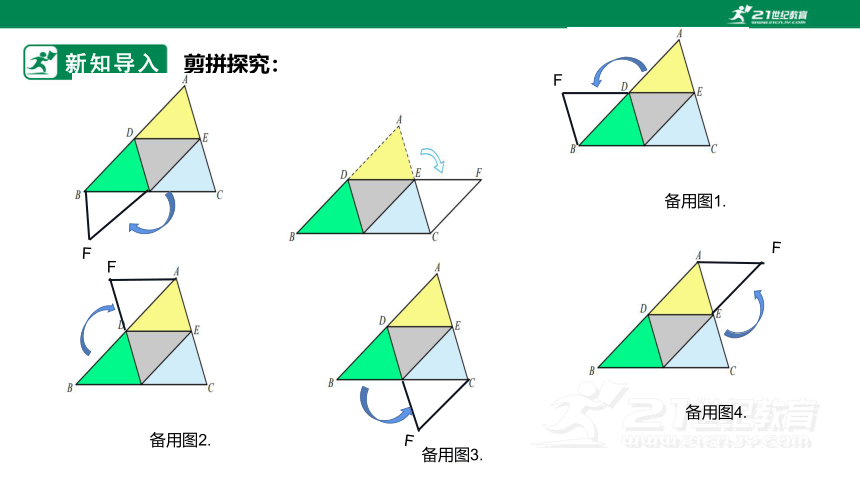
剪拼探究:
备用图1.
备用图2.
备用图3.
备用图4.
F
F
F
F
F
新知讲解
连接三角形两边中点的线段叫做三角形的中位线.
A
B
C
D
E
分享你的猜想,大声说出来:
三角形两边中点的连线
与第三边有怎样 的关系?
猜想:三角形的中位线平行于第三边,
且等于第三边的 一半.
新知讲解
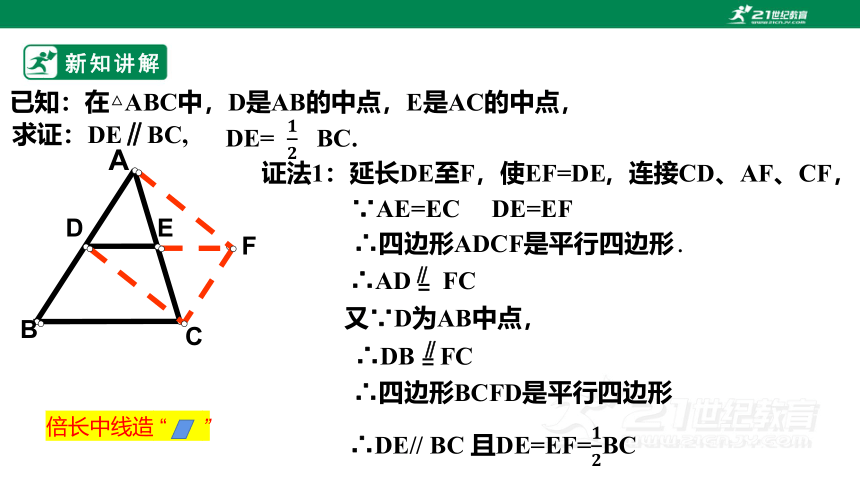
已知:在△ABC中,D是AB的中点,E是AC的中点,
求证:DE∥BC,
DE= BC.
A
B
C
E
D
F
证法1:延长DE至F,使EF=DE
,连接CD、AF、CF,
∵AE=EC DE=EF
∴四边形ADCF是平行四边形.
∴AD FC
=
∥
又∵D为AB中点,
∴DB FC
=
∥
∴四边形BCFD是平行四边形
倍长中线造 “ ”
∴DE// BC 且DE=EF=BC
.
新知讲解
A
B
C
E
D
F
证法2:过点C作AB的平行线交DE的延长线于F,
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,
∴DB FC
∴四边形BCFD是平行四边形.
∴DE// BC 且DE=EF=BC .
平行造等角
新知讲解
A
B
C
E
D
F
证法3:以点E为旋转中心,把△ADE绕点 E,按顺时针方向旋转1800,得△CFE,则D、E、F同在一条直线上,DE=EF,且△ADE≌△CFE
∴AD=CF,∠ADE=∠F
∴CF∥AB,
∵BD=AD=CF
∴DF BC ∴DE BC .
=
∥
=
∥
∴四边形BCFD是平行四边形
旋转出全等
新知讲解
C
E
D
B
A
三角形的中位线平行于第三边,且等于第三边的一半.
几何语言:
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
新知讲解
理解三角形的中位线定义的两层含义:
C
E
D
B
A
① 如果D、E分别为AB、AC的中点,
那么DE为△ABC的 ;
中位线
② 如果DE为△ABC的中位线,那么
D、E分别为AB、AC的 。
中点
新知讲解
定义:连结三角形两边中点的线段叫做三角形的中位线。
A
B
C
中点
D
中点
E
F
中点
1、一个三角形有几条中位线?,
三条。
2、三角形的中位线与中线有什么区别?
中位线是连结三角形两边中点的线段;
中线是连结一个顶点和它的对边中点的线段。
新知讲解
例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。
A
B
C
D
E
F
G
H
证明: 连接AC,
∵ EF是△ABC的中位线.
∴ EF//AC,EF= AC
同理:HG//AC,HG= AC
∴EF//HG,EF=HG
∴四边形EFGH是平行四边形
课堂总结
三角形的中位线
定义
连结三角形两边中点的线段叫做三角形的中位线
性质
三角形的中位线平行于第三边,并且等于第三边的一半
课堂练习
夯实基础,稳扎稳打
1、已知:DE是在△ABC中位线,则
(1)若∠ADE=65°,则∠B=____度.
(2)若BC=12cm,则DE=_____cm.
(3)若DE=7cm,则BC=______cm.
65
6
14
课堂练习
2、如图,已知△ABC中,AB = 3㎝,BC=3.4㎝, AC=4㎝
且D,E,F分别为 AC,AB,BC边的中点,
则△DEF的周长是 ㎝.
A
B
C
D
E
F
5.2
课堂练习
3、已知: 点D,E,F分别是△ABC三边的中点,则
(1)图中共有_____个平行四边形,
与△DEF全等的三角形有_____个
(2)若C△DEF =3,则C△ABC =____
(3)若S△DEF =6, 则S△ABC =_____
3
3
6
24
课堂练习
4.如图所示, ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5 ABCD的周长( )
A. 11 B. 13 C. 16 D. 22
D
课堂练习
5、如下图:在Rt △ ABC中,∠A=90°,
D、E、F分别是各边中点, AB=6cm,AC=8cm,
则△DEF的周长= cm .
E
F
B
A
C
D
12
课堂练习
连续递推,豁然开朗
6. 求证:三角形的一条中位线与第三边上的中线 互相平分.
已知:△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE与DF互相平分.
F
A
B
C
D
E
证明:连接DE、EF,
∵AD=DB,BE=EC,
∴DE ∥AC
(三角形的中位线平行于第三边且等于第三边的一半)
同理EF ∥AB。
∴四边形ADEF是平行四边形。
∴AE、DF互相平分(平行四边形的对角线互相平分)
课堂练习
7.如图所示,在三角形ABC中,AD是三角形ABC中∠BAC的角平分线, BD⊥AD,点D是垂足,点E是边BC的中点,如果AB=6,AC=14,求DE的长
F
中点的联想:
1、等腰三角形--------三线合一
2、直角三角形斜边中点--------三连等
3、三角形中两边中点-------中位线定理
分析:1.二线合一--------等腰三角形------
2.二边中点--------中位线定理
AD具有双重性:角平分线+垂线
6
6
14-6=8
8=4
.
三线合一
课堂练习
8.已知:在四边形ABCD中,AD=BC,P是对角线BD的中点,
M是DC的中点,N是AB的中点.求证∠1=∠2.
分析法:执果索因
要证:∠1=∠2
要证:PN=PM
要证:PN=
PM=
要证:AD=BC,P是BD的中点,
M是DC的中点,N是AB的中点.
要证: PN
.
课堂练习
9.已知 :如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和
等边三角形ACN.D,E,F分别是MB,BC,CN的中点,连接DE,FE.求证:DE=FE
F
A
B
C
D
E
M
N
600
600
分析法:执果索因
要证:DE=FE
要证:=
EF= BN
易证:△CMA≌△NBA(SAS)
要证:=BN
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.5 三角形的中位线
浙教版八下数学
新知导入
1.在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段, 叫做三角形的角平分线.
A
B
C
D
∵AD是△ABC的角平分线,
∴∠BAD =∠CAD =
∠BAC.
2.在三角形中,连结三角形的一个顶点与该顶点对边中点的线段,叫做这个三角形的中线.
A
D
C
B
∵AD是△ABC的中线,
∴BD=CD= BC
新知导入
3.从三角形的一个顶点向它的对边所在的直线作垂线,
顶点和垂足之间的线段叫做三角形的高线。
A
B
C
A
B
C
A
B
C
D
E
F
锐角三角形的垂心O在三角形内.
D
直角三角形的垂心就是直角顶点B.
F
D
E
P
钝角三角形的垂心P在三角形外.
三角形的三条高线的交点叫做三角形的垂心
O
新知导入
A
B
C
D
O
4.平行四边形的性质:
(1)从边看:对边相等且平行
(2)从角看:对角相等,邻角互补
(3)从对角线看:对角线互相平分
(4) 从对称性看:是中心对称图形.
(5) 推论:夹在两条平行线间的平行线段相等。
两条平行线间的距离处处相等。
新知导入
5. 怎样将一张三角形硬纸片剪成两部分,
使分成的两部分能拼成一个平行四边形
新知导入
剪拼探究:
备用图1.
备用图2.
备用图3.
备用图4.
F
F
F
F
F
新知讲解
连接三角形两边中点的线段叫做三角形的中位线.
A
B
C
D
E
分享你的猜想,大声说出来:
三角形两边中点的连线
与第三边有怎样 的关系?
猜想:三角形的中位线平行于第三边,
且等于第三边的 一半.
新知讲解
已知:在△ABC中,D是AB的中点,E是AC的中点,
求证:DE∥BC,
DE= BC.
A
B
C
E
D
F
证法1:延长DE至F,使EF=DE
,连接CD、AF、CF,
∵AE=EC DE=EF
∴四边形ADCF是平行四边形.
∴AD FC
=
∥
又∵D为AB中点,
∴DB FC
=
∥
∴四边形BCFD是平行四边形
倍长中线造 “ ”
∴DE// BC 且DE=EF=BC
.
新知讲解
A
B
C
E
D
F
证法2:过点C作AB的平行线交DE的延长线于F,
∵CF∥AB,
∴∠A=∠ECF
又AE=EC,∠AED=∠CEF
∴△ADE≌△CFE
∴ AD=FC
又DB=AD,
∴DB FC
∴四边形BCFD是平行四边形.
∴DE// BC 且DE=EF=BC .
平行造等角
新知讲解
A
B
C
E
D
F
证法3:以点E为旋转中心,把△ADE绕点 E,按顺时针方向旋转1800,得△CFE,则D、E、F同在一条直线上,DE=EF,且△ADE≌△CFE
∴AD=CF,∠ADE=∠F
∴CF∥AB,
∵BD=AD=CF
∴DF BC ∴DE BC .
=
∥
=
∥
∴四边形BCFD是平行四边形
旋转出全等
新知讲解
C
E
D
B
A
三角形的中位线平行于第三边,且等于第三边的一半.
几何语言:
∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.
2
1
新知讲解
理解三角形的中位线定义的两层含义:
C
E
D
B
A
① 如果D、E分别为AB、AC的中点,
那么DE为△ABC的 ;
中位线
② 如果DE为△ABC的中位线,那么
D、E分别为AB、AC的 。
中点
新知讲解
定义:连结三角形两边中点的线段叫做三角形的中位线。
A
B
C
中点
D
中点
E
F
中点
1、一个三角形有几条中位线?,
三条。
2、三角形的中位线与中线有什么区别?
中位线是连结三角形两边中点的线段;
中线是连结一个顶点和它的对边中点的线段。
新知讲解
例1、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH是平行四边形。
A
B
C
D
E
F
G
H
证明: 连接AC,
∵ EF是△ABC的中位线.
∴ EF//AC,EF= AC
同理:HG//AC,HG= AC
∴EF//HG,EF=HG
∴四边形EFGH是平行四边形
课堂总结
三角形的中位线
定义
连结三角形两边中点的线段叫做三角形的中位线
性质
三角形的中位线平行于第三边,并且等于第三边的一半
课堂练习
夯实基础,稳扎稳打
1、已知:DE是在△ABC中位线,则
(1)若∠ADE=65°,则∠B=____度.
(2)若BC=12cm,则DE=_____cm.
(3)若DE=7cm,则BC=______cm.
65
6
14
课堂练习
2、如图,已知△ABC中,AB = 3㎝,BC=3.4㎝, AC=4㎝
且D,E,F分别为 AC,AB,BC边的中点,
则△DEF的周长是 ㎝.
A
B
C
D
E
F
5.2
课堂练习
3、已知: 点D,E,F分别是△ABC三边的中点,则
(1)图中共有_____个平行四边形,
与△DEF全等的三角形有_____个
(2)若C△DEF =3,则C△ABC =____
(3)若S△DEF =6, 则S△ABC =_____
3
3
6
24
课堂练习
4.如图所示, ABCD的对角线AC,BD相交于点O,AE=EB,OE=3,AB=5 ABCD的周长( )
A. 11 B. 13 C. 16 D. 22
D
课堂练习
5、如下图:在Rt △ ABC中,∠A=90°,
D、E、F分别是各边中点, AB=6cm,AC=8cm,
则△DEF的周长= cm .
E
F
B
A
C
D
12
课堂练习
连续递推,豁然开朗
6. 求证:三角形的一条中位线与第三边上的中线 互相平分.
已知:△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE与DF互相平分.
F
A
B
C
D
E
证明:连接DE、EF,
∵AD=DB,BE=EC,
∴DE ∥AC
(三角形的中位线平行于第三边且等于第三边的一半)
同理EF ∥AB。
∴四边形ADEF是平行四边形。
∴AE、DF互相平分(平行四边形的对角线互相平分)
课堂练习
7.如图所示,在三角形ABC中,AD是三角形ABC中∠BAC的角平分线, BD⊥AD,点D是垂足,点E是边BC的中点,如果AB=6,AC=14,求DE的长
F
中点的联想:
1、等腰三角形--------三线合一
2、直角三角形斜边中点--------三连等
3、三角形中两边中点-------中位线定理
分析:1.二线合一--------等腰三角形------
2.二边中点--------中位线定理
AD具有双重性:角平分线+垂线
6
6
14-6=8
8=4
.
三线合一
课堂练习
8.已知:在四边形ABCD中,AD=BC,P是对角线BD的中点,
M是DC的中点,N是AB的中点.求证∠1=∠2.
分析法:执果索因
要证:∠1=∠2
要证:PN=PM
要证:PN=
PM=
要证:AD=BC,P是BD的中点,
M是DC的中点,N是AB的中点.
要证: PN
.
课堂练习
9.已知 :如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和
等边三角形ACN.D,E,F分别是MB,BC,CN的中点,连接DE,FE.求证:DE=FE
F
A
B
C
D
E
M
N
600
600
分析法:执果索因
要证:DE=FE
要证:=
EF= BN
易证:△CMA≌△NBA(SAS)
要证:=BN
.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
