4.6 反证法 课件(共21张PPT)

(共21张PPT)
4.6 反证法
浙教版八下数学
新知导入
新知导入
路边苦李
王戎7岁时，与小伙伴们外出游玩，看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子，只有王戎站在原地不动.有人问王戎为什么
王戎回答说:“树在道边而多子，此必苦李.”
小伙伴摘取一个尝了一下，果然是苦李.
王戎是怎样知道李子是苦的呢 他运用了怎样的推理方法
新知导入
王戎推理方法:
反设
假设“李子甜”
推理
树在道边则李子少
矛盾
与已知条件 “树在道边而多子”产生矛盾
反设不成立
假设 “李子甜”不成立
原命题成立
“树在道边而多子，此必为苦李” 是正确的
新知讲解
在证明一个命题时，人们有时先假设命题不成立，从这样的假设出发，经过推理得出和已知条件矛盾，或者与定义、基本事实、定理等矛盾.从而得出假设命题不成立是错误的，即所求证的命题正确.这种证明方法叫做反证法.
基本事实：
（1）两点确定一条直线
（2）两点之间线段最短
（3）在同一平面内，过一点有且只有一条直线与这条直线垂直
（4）两条直线被第三条所截，如果同位角相等，那么这两条直线平行
（5）过直线外一点有且只有一条直线与这条直线平行
（6）两边及其夹角分别相等的两个三角形全等（SAS)
（7）两角及其夹边分别相等的两个三角形全等(ASA)
（8）三边分别相等的两个三角形全等（SSS)
一分钟背诵
新知讲解
1.证明：在△ABC中，若AB≠AC，
则∠B≠∠C.
A
B
C
假设李子是甜的
假设∠B=∠C
那么李子会被过路人摘去解渴,
则李子会很少，这与事实相矛盾。
那么AB=AC，
这与已知条件
AB≠AC相矛盾
假设不正确，则李子是苦的。
假设不正确，则∠B≠∠C
反设
新知讲解
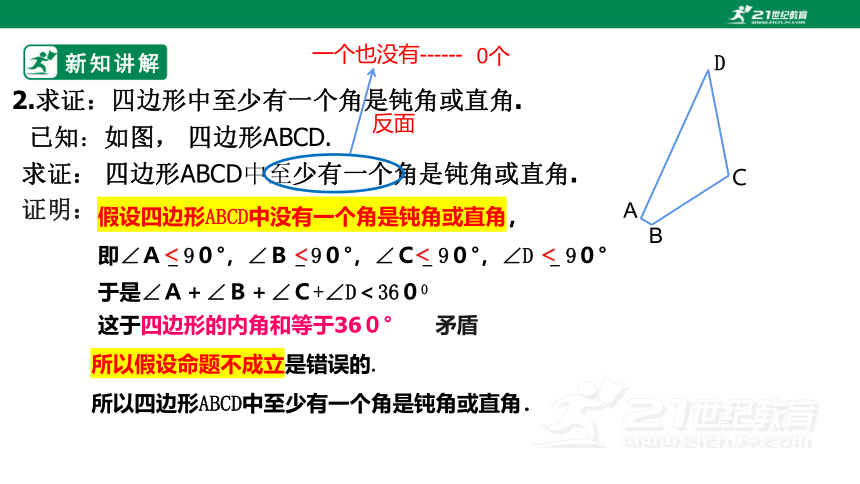
2.求证：四边形中至少有一个角是钝角或直角.
A
B
Ｃ
D
已知：如图， 四边形ABCD.
求证： 四边形ABCD中至少有一个角是钝角或直角.
证明：
假设四边形ABCD中没有一个角是钝角或直角，
即∠Ａ＿9０°，∠Ｂ＿9０°，∠Ｃ＿9０°，∠D ＿9０°
＜
＜
＜
＜
于是∠Ａ＋∠Ｂ＋∠Ｃ+∠D＜36０0
这于四边形的内角和等于36０° 矛盾
所以假设命题不成立是错误的.
所以四边形ABCD中至少有一个角是钝角或直角．
反面
一个也没有------
0个
反证法证明命题的一般步骤：反设——归谬——结论
(1)假设命题的结论不成立；
(2)从这个假设出发，经过推理论证，得出与公理、定理、定义或已知条件相矛盾；
(3)由矛盾断定所作假设不正确，从而得出原命题成立．
证明真命题 的方法
直接证法
间接证法
反证法
新知讲解
3.求证：在同一平面内，如果两条直线都和第三条直线平行，那么这两条直线也互相平行。
已知：a∥c, b∥c,求证：a∥b
a
b
c
M
证明：假设 a∥b
则a与b相交，设交点为M
∵a∥c, b∥c
∴过直线外一点M有两条直线a、b与c平行
这与
“过直线外一点有且只有一条直线与这条直线平行”
矛盾
∴假设不成立
∴a∥b
反设——归谬——结论
一开始的假设
课堂总结
准确地作出反设(即否定结论)是非常重要的，
下面是一些常见的结论的否定形式.
原词语 否定词 原词语 否定词
等于 任意的
是 至少有一个
都是 至多有一个
大于 至少有n个
小于 至多有n个
不等于
不是
不都是
不大于（≤）
不小于（≥）
某个
一个也没有（0个）
至少有两个（≥2）
至多有（n-1)个
至少有（n+1)个
课堂练习
1.用反证法证明“两直线平行，同位角相等”.
已知：AB∥CD，求证∠1=∠2.
证明:假设所求证的结论不成立
即 .
.
∴过点O作直线A'B'，使A'B'与EF所成的∠3与∠2相等，
∴直线A'B'与AB不重合
但A'B'∥CD（ ）
又已知AB∥CD
则 .
.
这与基本事实
产生矛盾
所以 ，
所求证的结论不成立
B'
A'
3
∠1 ∠2.
∠3 ∠1.
.
同位角相等，两直线平行
“过直线外一点有且只有一条直线与这条直线平行”
假设不成立
夯实基础，稳扎稳打
反设——归谬——结论
A
B
C
D
O
E
F
2
1
反证法：
2.证明：在 △ABC中，如果AB=c,BC=a, CA=b,且∠C ≠ 90° ，
那么a2 +b2 ≠ c2
A
B
C
a
反设——a2 +b2 = c2
结论——此命题是真命题。
归谬——则△ABC为直角三角形， ∠C =90°而和题设∠C ≠ 90°相矛盾。
b
c
课堂练习
已知：在△ABC中，AB≠AC,求证：∠B ≠ ∠ C
A
B
C
证明：假设　　　　　，
则　　　　　（　　　　　　　）
这与　　　　　　　　　矛盾．
假设不成立．
∴　　　　　　　　．
∠B ＝ ∠ C
AB＝AC
等角对等边
已知AB≠AC
∠B ≠ ∠ C
3.求证：在一个三角形中，如果两条边不相等，那么它们所对的角也不相等.
课堂练习
已知:
直线l1, l2, l3在同一平面内,且l1∥l2, l3与l1相交于点P.
求证:
l3与l2相交.
证明:
假设____________,那么_________.
因为已知_________,
所以过直线l2外一点P,有 和l2平行,
经过直线外一点,有且只有一条直线平行于已知直线
所以 ,即求证的命题正确.
这与“_______________________ ____________”矛盾.
l3与l2 不相交.
l3∥l2
l1∥l2
两条直线
假设不成立
l1
l2
l3
P
课堂练习
5.已知：两条不重合的直线AB,CD相交。求证AB,CD只有一个交点
证明：假设直线AB,CD 至少有两个交点，而且它们不 重合.
这和基 本事实“过两个已知点有且只有一条直线------两点确定一条直线”矛盾.
所以假设不成立，因此两条直线相交只有一个交点.
A
B
C
D
M
O
连续递推，豁然开朗
6.证明：在一个三角形中，至少有一个内角大于或等于60°.
已知：如图， △ＡＢＣ
A
B
C
求证： ∠Ａ，∠Ｂ，∠Ｃ中至少有一个内角大于或等于60°
证明：
假设△ＡＢＣ中没有一个内角大于或等于60°，
即 ∠Ａ＿＿ 60° ， ∠Ｂ＿＿ 60° ，∠Ｃ＿＿ 60°
＜
＜
＜
则　∠Ａ＋∠Ｂ＋∠Ｃ＿＿ 180°
＜
这与 “三角形的内角和等于180°”矛盾
所以假设不成立，
即所求证的结论成立．
在证明几何命题时，若从正面无法证明其结论时，往往是考虑从命题的反面入手来解决问题。从而体会数学的逆向思维。反证法是一种间接证明命题的方法。
一个也没有------
0个
7.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,
应假设 (　　)
A.没有锐角不大于45°
B.至多有一个锐角大于45°
C.两个锐角都不大于45°
D.两个锐角都小于45°
A
反面
没有----“0”个
8.已知：如图△ABC中，D、E两 点分别在AB和AC上
求证：CD、BE不能互相平分
证明：假设CD、BE互相平分
连结DE，
则四边形BCED是平行四边形
∴BD∥CE
这与BD、CE交于点A矛盾
假设不成立， ∴CD、BE不能互相平分
A
B
C
D
E
思维拓展，更上一层
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin