二次函数专题讲座[下学期]
图片预览



文档简介
二次函数专题讲座
思维基础:
(一)填空:
1.二次函数的图象的开口方向是向 ,顶点从标是 ,对称轴是 。
2.抛物线的顶点在x轴上,则m的值等于 .
3.如果把第一条抛物线向上平移个单位(a0),再向左平移个单位,就得到第二条抛物线,已知第一条抛物线过点(0,4),则第一条抛物线的函数关系式是 ________.
(二)选择:
1.如图代13-3-1所示二次函数的图象,则有( )
图代13-3-1 图代13-3-2
A.a+b+c0 B.a+b+c=0 C.a+b+c0 D.a+b+c的符号不定
2.如图1-3-2是抛物线的图象,则下列完全符合条件的是( )
A.a0,b0,c0,b24ac B.a0,b0,c0,b24ac
C.a0,b0,c0,b24ac D.a0,b0,c0,b24ac
3.已知抛物线的对称轴为x=1,与x轴、y轴的三个交点构成的三角形的面积为6,且与y轴的交点到原点的距离为3,则此二次函数的解析式为( )
A.或
B.或
C.或
D.或
学法指要:
例 在直角坐标系中,二次函数的图象与x轴交于A,B两点,与y轴交于点C,其中点A在点B的左边,若∠ACB=90°,.
(1) 求点C的坐标及这个二次函数的解析式;
(2) 试设计两种方案,作一条与y轴不生命,与△ABC的两边相交的直线,使截得的
三角形与△ABC相似,并且面积是△AOC面积的四分之一.
【思考】 (第一问)1.坐标轴上点的坐标有何特点?2.如何求抛物线与y轴的交
点坐标?3.如何设出抛物线与x轴的两个交点坐标?4.线段与坐标之间有何种关系?你会用坐标表示线段吗?
【思路分析】 本例必须准确设出A,B两点坐标,再求出C点坐标,并会用它们表
示线段的长,将代数问题转化为几何问题,再由几何问题转化为代数问题,相互转化,相互转化,水到渠成.
解:(1)依题意,设A(a,0),B(,0)其中a0, β0,则a,β是方程
∴△AOC∽△COB。
把A(-4,0)代入①,得
解这个方程得n=2.
∴所求的二次函数的解析式为
现在来解答第二问。
【思考】这第二问所要求作的三角形应具备什么条件?什么样的三角形与△ABC相似?在什么条件下可以讨论两个三角形面积的比?在一个图形上作一和直线,需要确定什么?△ABC是一个什么样的三角形?
【思路分析】①所求的三角形与△ABC相似;②所求的三角形面积=
所求三角形若与△ABC相似,要具备有“两角对应相等”,“两边对应成比例且夹角相等”,“三边对应成比例”等判定两三角形相似的条件。
在两三角形相似的条件下,“两三角形面积的比等于相似的平方”,即找相似比等于1:2.
在一个图形上,截得一个三角形,需要作一条直线,作一条直线应在图形上确定两个点,且这条直线不能与y轴重合。
分析至此问题十分明确,即在△ABC的两边上找出符合上述条件的两点作一条直线。
再来分析△ABC是一个什么样的三角形,猜测它是直角三角形最为理想。
从第一问得知的条件A(-4,0)B(1,0),C(0,-2)可用勾股定理推出,△ABC确是直角三角形。
这样△ABC∽△CAO∽△BCO,且为作符合条件的直线提供了条件。下边分述作符合条件直线的方案。
方案1:依据“三角形两边中点的连线,截得的三角形与原三角形相似”,其相似比是1:2,面积的比为1:4。
作法:取AO的中点D,过D作D D∥OC,
∴D是AC的中点。
∴ AD:AO=1:2,
即 △ADD=.
△ADD∽△ACO∽△ABC.
图代13-3-3
∴DD是所求作的直线,ADD是所求作的三角形。
方案2:利用∠C作一个△BCF △COB。
作法:在CA上截取CE,使CE=CO=2,在CB上截取CF,使CF=BO=1,连结EF,则△BCF即为所求,如图代13-3-4所示。请读者证明。
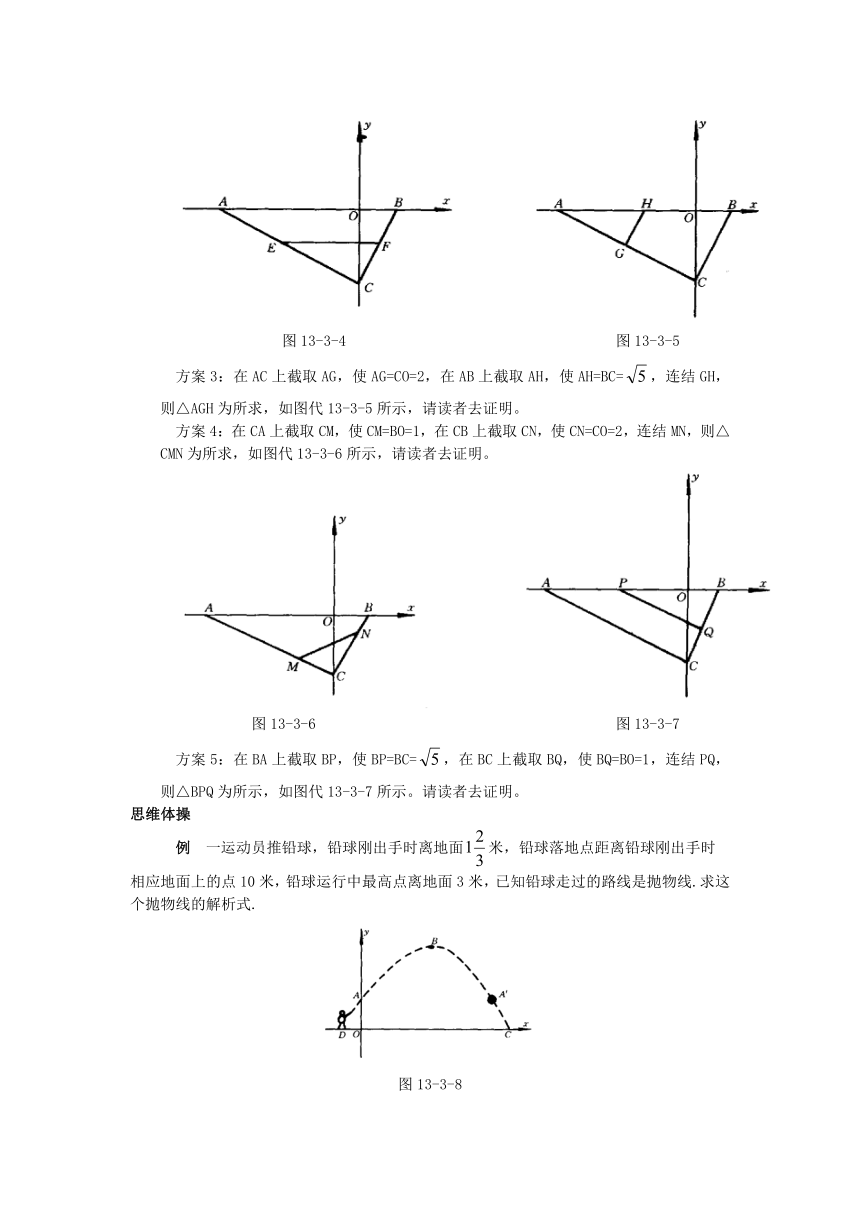
图13-3-4 图13-3-5
方案3:在AC上截取AG,使AG=CO=2,在AB上截取AH,使AH=BC=,连结GH,则△AGH为所求,如图代13-3-5所示,请读者去证明。
方案4:在CA上截取CM,使CM=BO=1,在CB上截取CN,使CN=CO=2,连结MN,则△CMN为所求,如图代13-3-6所示,请读者去证明。
图13-3-6 图13-3-7
方案5:在BA上截取BP,使BP=BC=,在BC上截取BQ,使BQ=BO=1,连结PQ,则△BPQ为所示,如图代13-3-7所示。请读者去证明。
思维体操
例 一运动员推铅球,铅球刚出手时离地面米,铅球落地点距离铅球刚出手时
相应地面上的点10米,铅球运行中最高点离地面3米,已知铅球走过的路线是抛物线.求这个抛物线的解析式.
图13-3-8
如图,结合题意,知抛物线过,用一般式:
解之,于是有
解方程组,得
;
.
∴所求抛物线解析式为
或.
∵,这时,抛物线的最高点(-20,3)不在运动员与铅球落地之间,不合题意,舍去.
∴所求抛物线解析式为
(0≤x≤10).
【扩散2】 仿扩散1知抛物线过.因B为顶点,所以利用顶点式最宜,于是可设抛物线的解析式为
.
又其图象过A,C两点,则
解方程组,得
;
.
∵抛物线最高点(-20,3)不在运动员和铅球之间,不合题意,∴舍去.
故所求抛物线的解析式是(0≤x≤10).
【扩散3】 抛物线与x轴交于两点,即D(x,0),C(10,0),联想截距式解之.
于是设抛物线解析式为,
其图象又过A,C两点,则有
,∴.
又
,
∴ . ②
①②联立解方程组,得
;
.
但不合题意,舍去.
故所求二次函数解析式为(0≤x≤10).
【扩散4】 由抛物线对称性,设对称点,B(m,3),又C(10,0),应用一般式可获解.
设抛物线,则可得
解这个方程组,得
.
∵(m,3)在第一象限,∴m0.
∴m=-20(舍去),∴m=4.
进而求得:
故所求抛物线解析式是:(0≤x≤10).
【扩散5】 如图,这是某空防部队进行射击训练时在平面直角坐标系中的示意图,在地面O,A两个观测点测得空中固定目标C的仰角分别为α和β,OA=1千米,tgα=,tgβ=,位于O点正上方千米D点处的直升飞机向目标C发射防空导弹,该导弹运行达到距地面最大高度3千米时,相应的水平距离为4千米(即图中的E点).
(1) 若导弹运行轨道为一抛物线,求该抛物线的解析式;
(2) 说明按(1)中轨道运行的导弹能否击中目标C的理由.
【思路分析】
1 本例应用扩散1~4思路均可,尤以扩散2应用顶点式最佳,读者可仿扩散2求得抛
物线解析式为:(0≤x≤10).
2 过点C作CB⊥Ox,垂足为B,然后解Rt△OBC和Rt△ABC,可求得点在抛
物线上,因此可击中目标C(请读者自己写出完整解答过程).
【扩散6】 有一抛物线形的立交桥拱,这个桥拱的最大高度为16m,跨度为40m,现
把它的图形放在坐标系里(如图所示),若在离跨度中心M点5m处垂直竖直一铁柱支撑拱顶,这铁柱应取多长?
图代13-3-9
【思路分析】 本例仿扩散2可设抛物线解析式为(0≤x≤40),
又抛物线过原点,进而求得,在距离M点5m处,即它们的横坐标是x1=15或x2=25,分别代入抛物线解析式,求得y1=y2=15.所以铁柱应取15m长.
【评析】 由扩散1~6,抛物线应用从体育方面,扩散到军事,涉及现代科技、导弹、
直升飞机等.进而又扩散到桥梁建筑,涉及到现代化建设的方方面面,告诉同学们,必须学好课本知识,才能适应现代化的需要.
图13-3-10
本例的解题思路扩散,把顶点式、一般式、截距式、抛物线的对称性都进行了展示,
我们可以根据不同的情况,迅速进行决策,选设不同的解析式,达到求解的目的.
心中有数:
二次函数的知识,是初中三年级数学的重点内容.在解有关二次函数的问题时,应用待
定系数法和方程、方程组的知识,用到数形结合、观察、想象的思想方法,应当深入理解和掌握这部分知识.
动手动脑:
1. 某商人如果将进货价为8元的商品按每件10元出售时,每天可销售100件,现在采
用提高售出价,减少进货量的办法增加利润,已知这种商品每件提高1元,其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚利润为最大,并求出最大利润?
2. 已知抛物线与x轴交于A,B两点,与y轴交于C点,若
△ABC是等腰三角形,求抛物线的解析式.
3. 已知抛物线.
(1)求证:不论m取何值,抛物线与x轴必有两个交点,并且有一个交点是A(2,0).
(2)设抛物线与x轴的另一个交点为B,AB的长为d,求d与m之间的函数关系式.
(3) 当d=10,P(a,b)为抛物线上一点.
①当△ABP是直角三角形时,求b的值;
②当△APB是锐角三角形、钝角三角形时,分别写出b的范围(不要求写出解答过程).
创新园地:
如图,有一模型拱门,其拱门的徒刑为抛物线的一部分(该抛物线为二次函数
的图形),拱门宽AB=20cm,拱门高PO为8cm,已知小明的玩具车宽为12cm,车高hcm,就能顺利通过这拱门,那么满足这个条件h的最大整数为 .
提示:本例没有告知拱门所在坐标,这就需要我们自己建立直角坐标系后求解.
图13-3-11
思维基础:
(一)填空:
1.二次函数的图象的开口方向是向 ,顶点从标是 ,对称轴是 。
2.抛物线的顶点在x轴上,则m的值等于 .
3.如果把第一条抛物线向上平移个单位(a0),再向左平移个单位,就得到第二条抛物线,已知第一条抛物线过点(0,4),则第一条抛物线的函数关系式是 ________.
(二)选择:
1.如图代13-3-1所示二次函数的图象,则有( )
图代13-3-1 图代13-3-2
A.a+b+c0 B.a+b+c=0 C.a+b+c0 D.a+b+c的符号不定
2.如图1-3-2是抛物线的图象,则下列完全符合条件的是( )
A.a0,b0,c0,b24ac B.a0,b0,c0,b24ac
C.a0,b0,c0,b24ac D.a0,b0,c0,b24ac
3.已知抛物线的对称轴为x=1,与x轴、y轴的三个交点构成的三角形的面积为6,且与y轴的交点到原点的距离为3,则此二次函数的解析式为( )
A.或
B.或
C.或
D.或
学法指要:
例 在直角坐标系中,二次函数的图象与x轴交于A,B两点,与y轴交于点C,其中点A在点B的左边,若∠ACB=90°,.
(1) 求点C的坐标及这个二次函数的解析式;
(2) 试设计两种方案,作一条与y轴不生命,与△ABC的两边相交的直线,使截得的
三角形与△ABC相似,并且面积是△AOC面积的四分之一.
【思考】 (第一问)1.坐标轴上点的坐标有何特点?2.如何求抛物线与y轴的交
点坐标?3.如何设出抛物线与x轴的两个交点坐标?4.线段与坐标之间有何种关系?你会用坐标表示线段吗?
【思路分析】 本例必须准确设出A,B两点坐标,再求出C点坐标,并会用它们表
示线段的长,将代数问题转化为几何问题,再由几何问题转化为代数问题,相互转化,相互转化,水到渠成.
解:(1)依题意,设A(a,0),B(,0)其中a0, β0,则a,β是方程
∴△AOC∽△COB。
把A(-4,0)代入①,得
解这个方程得n=2.
∴所求的二次函数的解析式为
现在来解答第二问。
【思考】这第二问所要求作的三角形应具备什么条件?什么样的三角形与△ABC相似?在什么条件下可以讨论两个三角形面积的比?在一个图形上作一和直线,需要确定什么?△ABC是一个什么样的三角形?
【思路分析】①所求的三角形与△ABC相似;②所求的三角形面积=
所求三角形若与△ABC相似,要具备有“两角对应相等”,“两边对应成比例且夹角相等”,“三边对应成比例”等判定两三角形相似的条件。
在两三角形相似的条件下,“两三角形面积的比等于相似的平方”,即找相似比等于1:2.
在一个图形上,截得一个三角形,需要作一条直线,作一条直线应在图形上确定两个点,且这条直线不能与y轴重合。
分析至此问题十分明确,即在△ABC的两边上找出符合上述条件的两点作一条直线。
再来分析△ABC是一个什么样的三角形,猜测它是直角三角形最为理想。
从第一问得知的条件A(-4,0)B(1,0),C(0,-2)可用勾股定理推出,△ABC确是直角三角形。
这样△ABC∽△CAO∽△BCO,且为作符合条件的直线提供了条件。下边分述作符合条件直线的方案。
方案1:依据“三角形两边中点的连线,截得的三角形与原三角形相似”,其相似比是1:2,面积的比为1:4。
作法:取AO的中点D,过D作D D∥OC,
∴D是AC的中点。
∴ AD:AO=1:2,
即 △ADD=.
△ADD∽△ACO∽△ABC.
图代13-3-3
∴DD是所求作的直线,ADD是所求作的三角形。
方案2:利用∠C作一个△BCF △COB。
作法:在CA上截取CE,使CE=CO=2,在CB上截取CF,使CF=BO=1,连结EF,则△BCF即为所求,如图代13-3-4所示。请读者证明。
图13-3-4 图13-3-5
方案3:在AC上截取AG,使AG=CO=2,在AB上截取AH,使AH=BC=,连结GH,则△AGH为所求,如图代13-3-5所示,请读者去证明。
方案4:在CA上截取CM,使CM=BO=1,在CB上截取CN,使CN=CO=2,连结MN,则△CMN为所求,如图代13-3-6所示,请读者去证明。
图13-3-6 图13-3-7
方案5:在BA上截取BP,使BP=BC=,在BC上截取BQ,使BQ=BO=1,连结PQ,则△BPQ为所示,如图代13-3-7所示。请读者去证明。
思维体操
例 一运动员推铅球,铅球刚出手时离地面米,铅球落地点距离铅球刚出手时
相应地面上的点10米,铅球运行中最高点离地面3米,已知铅球走过的路线是抛物线.求这个抛物线的解析式.
图13-3-8
如图,结合题意,知抛物线过,用一般式:
解之,于是有
解方程组,得
;
.
∴所求抛物线解析式为
或.
∵,这时,抛物线的最高点(-20,3)不在运动员与铅球落地之间,不合题意,舍去.
∴所求抛物线解析式为
(0≤x≤10).
【扩散2】 仿扩散1知抛物线过.因B为顶点,所以利用顶点式最宜,于是可设抛物线的解析式为
.
又其图象过A,C两点,则
解方程组,得
;
.
∵抛物线最高点(-20,3)不在运动员和铅球之间,不合题意,∴舍去.
故所求抛物线的解析式是(0≤x≤10).
【扩散3】 抛物线与x轴交于两点,即D(x,0),C(10,0),联想截距式解之.
于是设抛物线解析式为,
其图象又过A,C两点,则有
,∴.
又
,
∴ . ②
①②联立解方程组,得
;
.
但不合题意,舍去.
故所求二次函数解析式为(0≤x≤10).
【扩散4】 由抛物线对称性,设对称点,B(m,3),又C(10,0),应用一般式可获解.
设抛物线,则可得
解这个方程组,得
.
∵(m,3)在第一象限,∴m0.
∴m=-20(舍去),∴m=4.
进而求得:
故所求抛物线解析式是:(0≤x≤10).
【扩散5】 如图,这是某空防部队进行射击训练时在平面直角坐标系中的示意图,在地面O,A两个观测点测得空中固定目标C的仰角分别为α和β,OA=1千米,tgα=,tgβ=,位于O点正上方千米D点处的直升飞机向目标C发射防空导弹,该导弹运行达到距地面最大高度3千米时,相应的水平距离为4千米(即图中的E点).
(1) 若导弹运行轨道为一抛物线,求该抛物线的解析式;
(2) 说明按(1)中轨道运行的导弹能否击中目标C的理由.
【思路分析】
1 本例应用扩散1~4思路均可,尤以扩散2应用顶点式最佳,读者可仿扩散2求得抛
物线解析式为:(0≤x≤10).
2 过点C作CB⊥Ox,垂足为B,然后解Rt△OBC和Rt△ABC,可求得点在抛
物线上,因此可击中目标C(请读者自己写出完整解答过程).
【扩散6】 有一抛物线形的立交桥拱,这个桥拱的最大高度为16m,跨度为40m,现
把它的图形放在坐标系里(如图所示),若在离跨度中心M点5m处垂直竖直一铁柱支撑拱顶,这铁柱应取多长?
图代13-3-9
【思路分析】 本例仿扩散2可设抛物线解析式为(0≤x≤40),
又抛物线过原点,进而求得,在距离M点5m处,即它们的横坐标是x1=15或x2=25,分别代入抛物线解析式,求得y1=y2=15.所以铁柱应取15m长.
【评析】 由扩散1~6,抛物线应用从体育方面,扩散到军事,涉及现代科技、导弹、
直升飞机等.进而又扩散到桥梁建筑,涉及到现代化建设的方方面面,告诉同学们,必须学好课本知识,才能适应现代化的需要.
图13-3-10
本例的解题思路扩散,把顶点式、一般式、截距式、抛物线的对称性都进行了展示,
我们可以根据不同的情况,迅速进行决策,选设不同的解析式,达到求解的目的.
心中有数:
二次函数的知识,是初中三年级数学的重点内容.在解有关二次函数的问题时,应用待
定系数法和方程、方程组的知识,用到数形结合、观察、想象的思想方法,应当深入理解和掌握这部分知识.
动手动脑:
1. 某商人如果将进货价为8元的商品按每件10元出售时,每天可销售100件,现在采
用提高售出价,减少进货量的办法增加利润,已知这种商品每件提高1元,其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚利润为最大,并求出最大利润?
2. 已知抛物线与x轴交于A,B两点,与y轴交于C点,若
△ABC是等腰三角形,求抛物线的解析式.
3. 已知抛物线.
(1)求证:不论m取何值,抛物线与x轴必有两个交点,并且有一个交点是A(2,0).
(2)设抛物线与x轴的另一个交点为B,AB的长为d,求d与m之间的函数关系式.
(3) 当d=10,P(a,b)为抛物线上一点.
①当△ABP是直角三角形时,求b的值;
②当△APB是锐角三角形、钝角三角形时,分别写出b的范围(不要求写出解答过程).
创新园地:
如图,有一模型拱门,其拱门的徒刑为抛物线的一部分(该抛物线为二次函数
的图形),拱门宽AB=20cm,拱门高PO为8cm,已知小明的玩具车宽为12cm,车高hcm,就能顺利通过这拱门,那么满足这个条件h的最大整数为 .
提示:本例没有告知拱门所在坐标,这就需要我们自己建立直角坐标系后求解.
图13-3-11
同课章节目录
