5.1矩形(3) 课件

课件21张PPT。义务教育课程标准实验教科书　
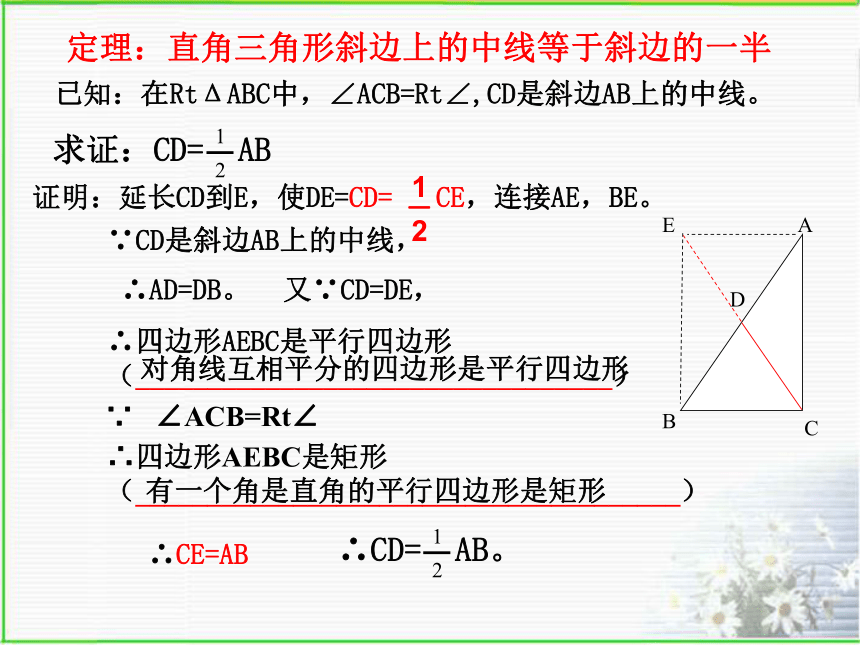
浙江版《数学》八年级下册6.1 矩形 (3)回顾：矩形有哪些性质？∠ABC=∠BCD=∠ADC=∠BAD=90OOA=OB=OC=OD（1）从边看：对边平行且相等（2）从角看：四个角都是直角（3）从对角线看：对角线互相平分且相等（2）有一个角是直角的平行四边形是矩形。 （1）有三个角是直角的四边形是矩形。（3）对角线相等的平行四边形是矩形。回顾：矩形的判定方法： 直角三角形斜边上的中线等于斜边的一半。请你证明 定理：直角三角形斜边上的中线等于斜边的一半 已知：在RtΔABC中，∠ACB=Rt∠,CD是斜边AB上的中线。ACBDE证明：延长CD到E，使DE=CD= CE，连接AE，BE。 ∵CD是斜边AB上的中线，∴AD=DB。又∵CD=DE，∴四边形AEBC是平行四边形
（_________________________________）∴CE=AB∵ ∠ACB=Rt∠∴四边形AEBC是矩形
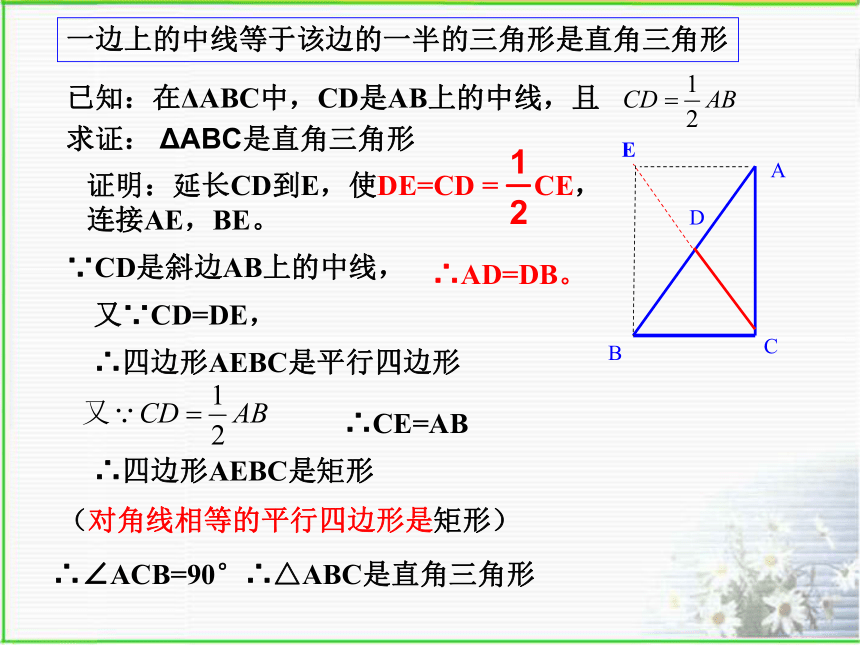
（______________________________________）有一个角是直角的平行四边形是矩形对角线互相平分的四边形是平行四边形一边上的中线等于该边的一半的三角形是直角三角形已知：在ΔABC中，CD是AB上的中线，且求证： ΔABC是直角三角形证明：延长CD到E，使DE=CD = CE，
连接AE，BE。 ∵CD是斜边AB上的中线，∴AD=DB。又∵CD=DE，∴四边形AEBC是平行四边形∴CE=ABDE∴四边形AEBC是矩形∴∠ACB=90°∴△ABC是直角三角形（对角线相等的平行四边形是矩形）小结：证明一条线段是另一条线段的1/2或2倍，
（１）常用的定理：（2）添辅助线的方法：“三角形的中位线定理”和“直角三角形的斜边上的中线等于斜边的一半”延长短的一倍，再证它与长的线段相等；
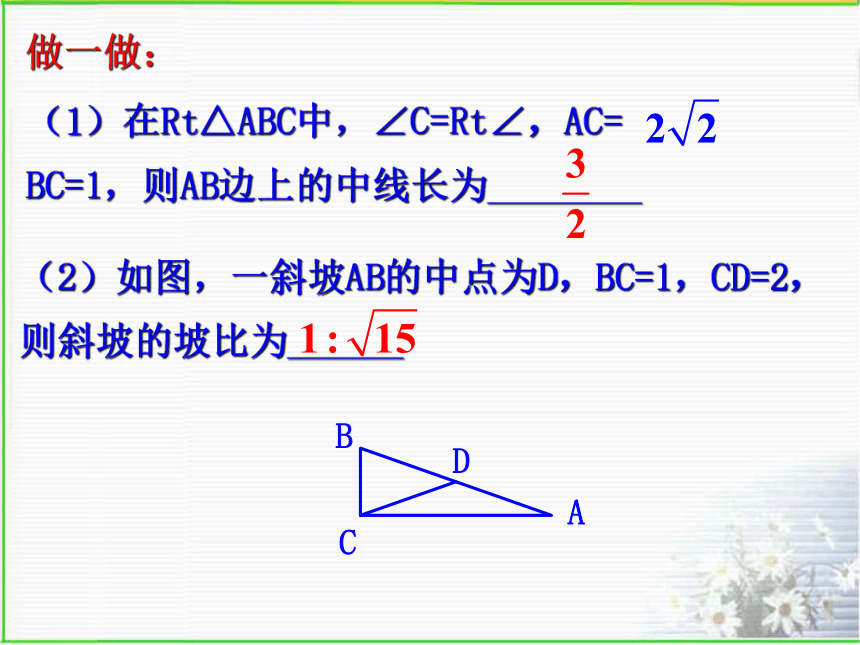
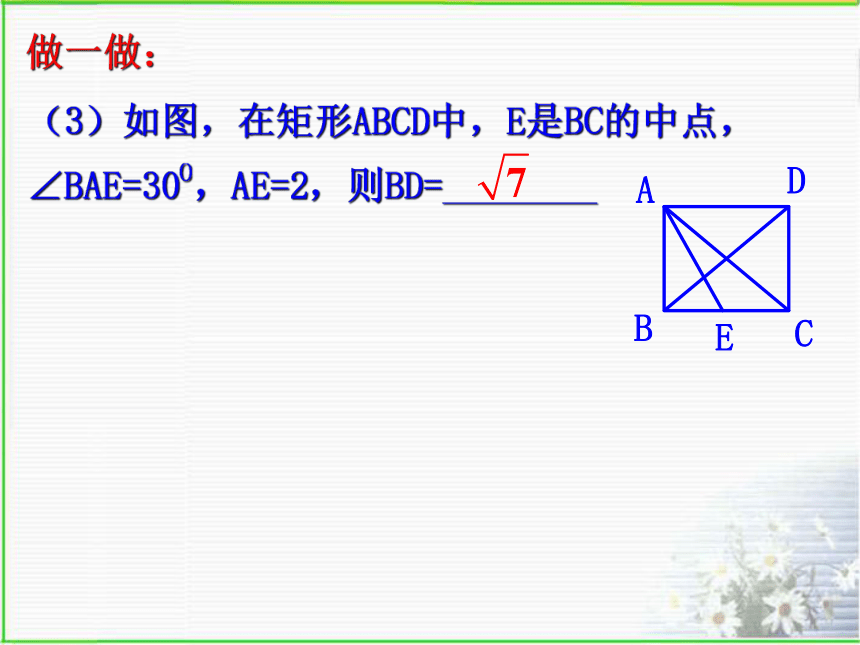
或在长的上截取中点,再证中点取得的一半等于短的，（2）如图，一斜坡AB的中点为D，BC=1，CD=2，则斜坡的坡比为______做一做：（1）在Rt△ABC中，∠C=Rt∠，AC=BC=1，则AB边上的中线长为________做一做：（3）如图，在矩形ABCD中，E是BC的中点，∠BAE=30O，AE=2，则BD=________做一做：（1）在Rt△ABC中，∠C=Rt∠，AC=BC=1，则AB边上的中线长为________(2)如图Ｒt⊿ABC中，∠ＡＣＢ＝９０°，点Ｄ，Ｆ分别是ＡＣ，ＢＣ边上的中点，点Ｅ是ＡＢ边上的中点，如果ＣＥ＝３，则ＤＦ＝＿＿＿3 （３）、 如图：在RtΔABC中，CD是斜边AB上的中线，已知∠DCA=200，则∠ A ＝＿＿，∠B＝____。20°70°(4)一张平行四边形的木板如图，现要求剪一刀，把它分成两部分，然后作适当的图形变换，把剪开的两部分拼成一个矩形。说明你的剪法和所采用的变换。E解：过A作AＥ垂直ＢC于点Ｅ，沿AＥ剪一刀，然后把⊿ＡBＥ向右平移，
使ＡB和ＣD重合．F例1：已知：如图，△ABC中，BD，CE是高，G、F分别是BC，DE的中点。试判断FG与DE的位置关系，并加以证明。变式：已知：如图，在四边形ABCD中，∠ABC= ∠ADC=Rt∠，M是AC的中点，N是BD的中点。试判断MN与BD的位置关系，并加以证明。根据我们以前所学习过的知识、培养的能力。完成下题在Rt△ ABC中，∠ C=900，AC=1/2AB，试猜想∠ B的度数。BAC解：作斜边AB上的中线CD 从上面题你可以总结、归结出什么结论？它可以作为一条定理用吗？可以在填空、选择题中用来解题吗？ 结论：在直角三角形中，等于斜边一半的直角边所对的角等于300
它只限于用在填空、选择题中用来解题3、在矩形ABCD中，E是BC上一点，已知AE=AD,DF垂直与AE于点F,求证：CE=FE4、以?ABC的三边在BC 的同侧分别作三个等边三角形，即?ABC,?BCE,?ACF,请回答下列问题：（1）四边形ADEF是什么四边形？（2）当?ABC满足什么条件时，四边形ADEF是矩形？FEDCBA如图，E是矩形ABCD边CB延长线上一点，CE＝CA，F是AE的中点。求证：BF⊥FD
体会.分享说能出你这节课的收获和体验让大家与你分享吗？课堂小结：证明一条线段是另一条线段的1/2或2倍，
（１）常用的定理：（2）添辅助线的方法： “三角形的中位线定理”和“直角三角形的斜边上的中线等于斜边的一半” 延长短的一倍，再证它与长的线段相等；或在长的上截取中点,再证中点取得的一半等于短的，例2：已知：如图，AB与直线 相交于一点，过点A，B作 于C， 于D，M为AB的中点，连结MC，MD。求证：MC=MDK 作 业（1）作业本
（2）课后作业题