5.2 菱形（1）课件 (共23张PPT)

(共23张PPT)
浙教版八年级下册
5.2 菱形 （1）
新知导入
一组邻边相等的平行四边形叫做菱形
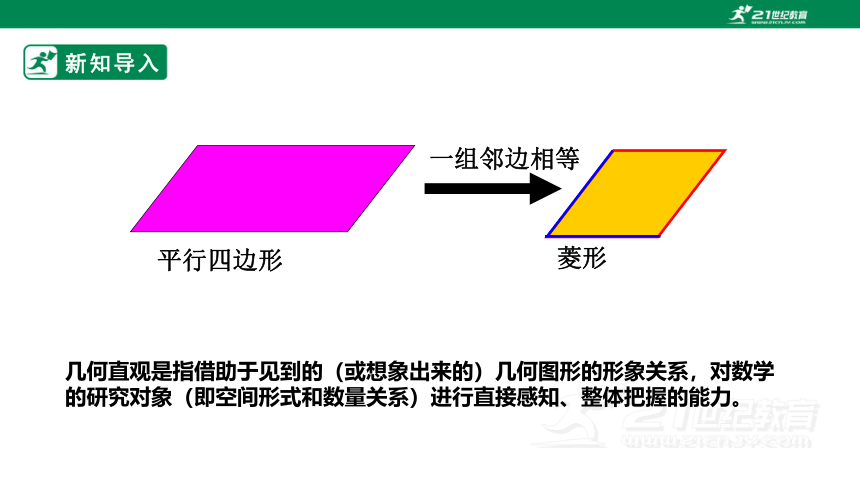
平行四边形
菱形
一组邻边相等
几何直观是指借助于见到的（或想象出来的）几何图形的形象关系，对数学的研究对象（即空间形式和数量关系）进行直接感知、整体把握的能力。
新知导入
几何直观，直接感知
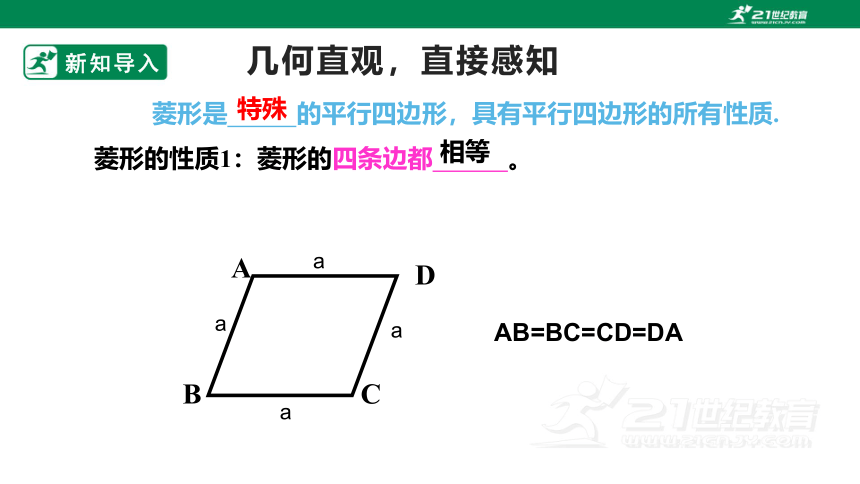
菱形是 的平行四边形，具有平行四边形的所有性质.
特殊
菱形的性质1：菱形的四条边都 。
相等
A
B
D
C
a
a
a
a
AB=BC=CD=DA
新知导入
新知导入
菱形:工整、匀称、美观
新知讲解
已知:如图，AC，BD是菱形ABCD的两条对角线，AC，BD相交于点O.
求证: （1）AC⊥BD;
（2）AC平分∠BAD和∠BCD,BD平分∠ADC 和∠ABC.
O
D
B
C
A
证明：
∵四边形ABCD是菱形
∴AD=CD，AO=CO
∵DO=DO
∴△AOD≌△COD(SSS)
∴∠AOD=∠COD=90°
∴AC⊥BD
∴∠ADO=∠CDO
∴BD平分∠ADC
同理，BD平分∠ABC,AC平分∠BAD和∠BCD
菱形是特殊的平行四边形，具有平行四边形的所有性质.
新知讲解
法二：
O
D
B
C
A
∵四边形ABCD是菱形，
∴AB=AD
(菱形的定义），
BO=DO
(平行四边形的对角线互相平分）
∴AC⊥BD，AC平分∠BAD
（等腰三角形三线合一）
同理，AC平分∠BCD，BD平分∠ABC和∠ADC
菱 形
转化
三角形
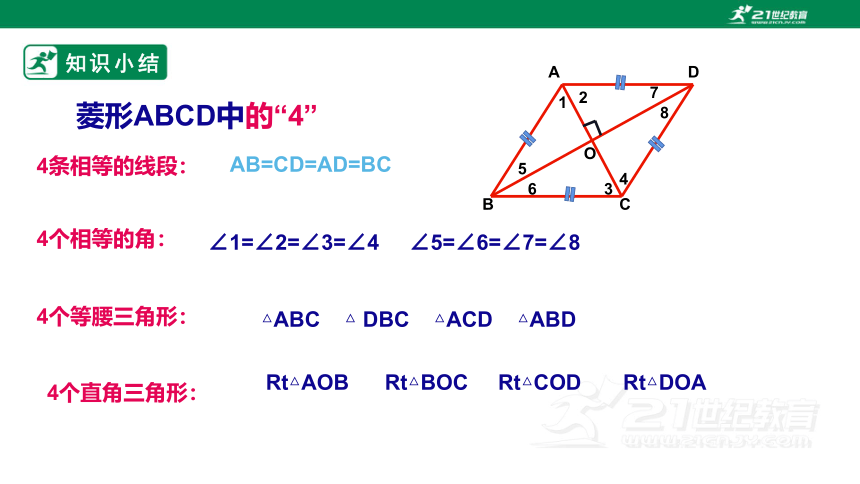
菱形ABCD中的“4”
A
B
C
D
O
1
2
3
4
5
6
7
8
4条相等的线段：
AB=CD=AD=BC
4个相等的角：
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
4个等腰三角形：
△ABC △ DBC △ACD △ABD
4个直角三角形：
Rt△AOB Rt△BOC Rt△COD Rt△DOA
知识小结
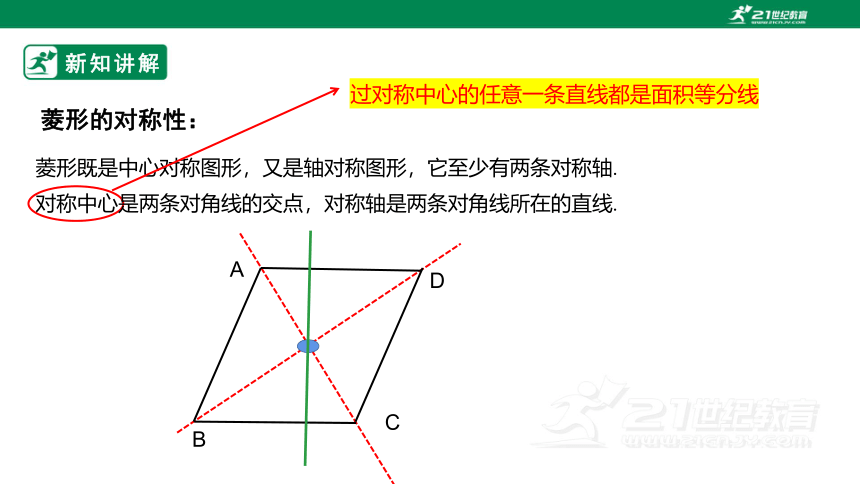
菱形的对称性：
菱形既是中心对称图形，又是轴对称图形，它至少有两条对称轴.
A
B
C
D
过对称中心的任意一条直线都是面积等分线
新知讲解
对称中心是两条对角线的交点，对称轴是两条对角线所在的直线.
菱形的性质
对角线
角
边
对称性
菱形的对边 且 .
平行
相等
菱形的四条边都 .
相等
菱形的对角 ，邻角 .
相等
互补
菱形的两条对角线互相 且 .
垂直
平分
菱形的每一条对角线平分一组 .
对角
中心对称：菱形的对角线的 就是对称中心
交点
轴对称：菱形至少有 条对称轴 即：两条对角线所在的直线
两
知识小结
一分钟背诵：菱形对角线性质
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6
1、求菱形的边长 2、求对角线AC的长.
解:∵四边形ABCD是菱形,
∴AB=AD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
∵∠BAC=30°∴∠BAD=60°
∴ABD是等边三角形.∴ AB=BD=6
又∵OB=OD=3(平行四边形的对角线互相平分)
AC⊥BD(菱形的对角线互相垂直)
由勾股定理,得AO=
AC=2AO=
新知讲解
A
B
C
D
O
法1： S菱形=
法2：S菱形 =
法3： S菱形 =
我非常喜欢直观和想象。经常把对数学中的一些内容看成是天然真实的“自然现象”，努力设法把学到的数学知识变成自己头脑中十分明显的直观形象。
E
BC ·AE
∟
∟
∟
A
B
C
D
求证：对角线互相垂直的四边形的面积
等于对角线乘积的一半。
S△ABD+S△BCD= AC·BD
.
已知：在四边形ABCD中，AC⊥BD,
求证：S四边形ABCD =
.
.
课堂练习
1.菱形具有而矩形不一定有的性质是( )
(A)对角线互相平分 (B)四条边都相等
(C)对角相等 (D)邻角互补
B
2.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F.求证:AE=AF.
夯实基础，稳扎稳打
法1：△ABE≌△ADF
法2：菱形ABCD面积算两次：BC
.
3.已知菱形 中，对角线 与 交于点O， ， ，则该菱形的周长是（ ）
A. 13 B. 52
C. 120 D. 240
B
课堂练习
课堂练习
4. 已知：如图，在菱形 中，点 分别在边 ，
上，且 ，连结 ， ．
求证： ．
证明：∵四边形 是菱形，
， .
在 与 中，
， ．
.
课堂练习
5.在菱形ABCD中,CE⊥AB于E,已知∠BCE=30°,CE=3cm.
求菱形ABCD的周长和面积.
BE=
300、600、900直角三角形配套数字：1：：2
BC=2
C菱形ABCD=8
.
S菱形ABCD=
.
连续递推，豁然开朗
6.如图，将 ABCD 沿AE 翻折，使点B 恰好落在AD上的点F 处，则下列结论不一定成立的是(　　)
A．AF＝EF
B．AB＝EF
C．AE＝AF
D．AF＝BE
C
菱形藏其中
7. 请利用两个全等的等腰（不 等边）三角形 纸片拼成一个平行四边形。
有几种拼法？其中有菱形？你是如何判定的
1、腰重合
2、底重合
课堂练习
几何直观：特殊图形藏其中
等边三角形ABD
8、已知如图，菱形ABCD中，E是AB的中点，且DE⊥AB，AB=2。
求（1）∠ABC的度数；
（2）对角线AC、BD的长；
（3）菱形ABCD的面积
课堂练习
（1）∠ABC=1200
(3) S菱形ABCD=
.
（2）AC=2，BD=2
.
思维拓展，更上一层
9. 菱形ABCD中,∠ABC=60°,AB=4cm,P为BD上任意一点,
E为BC中点,求PE+PC的最小值.
60°
⌒
∟
几何直观 ：直接感知，整体把握
PE+PC的最小值就是 .
直观是一种能透过现象看到本质、
一眼看出不同事物之间关联的洞察能力。
几何直观能告诉我们什么是可能重要、
可能有意义和可接近的，
并使我们在解题中免于陷入歧途之苦。
AE=2
.
思维拓展，更上一层
10： 已知,在菱形ABCD中,∠BAD= 120° ,现将一块含 60°角的三角尺AMN(其中∠NAM= 60°)叠放在菱形上,然后将三角尺绕点A旋转.在旋转过程中,设AM交边BC于点E,AN交边CD于点F,那么BE+DF与AB有着怎样的数量关系 请你借助几何直观，大胆猜想，小心求证。
几何直观：结论猜想 BE+DF=AB .
洞察力： 撇开无关要素，单刀直入把握要害；
透过现象看本质，一眼看出不同事物之间的关联 。
原因猜想: .
全等藏其中
法1：△ABE≌△ACF,
法2：△ACE≌△ADF
BE=CF
CE=DF
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin