5.2 矩形（2）

课件15张PPT。泰顺六中 翁怀新2014年5月15日5.1矩形(2)矩形有哪些性质？ 1.边:2.角:3. 对角线: 矩形两组对边分别平行.
矩形两组对边分别相等.矩形的四个角都是直角.矩形的对角线相等且互相平分.温故知新4.从对称看:矩形既是轴对称，又是中心对称.木工师傅
(1)测量两组对边,发现两组对边分别相等;
(2)将直角尺靠紧窗框的一个角,测得这是直角.
由此说明这个窗框是矩形
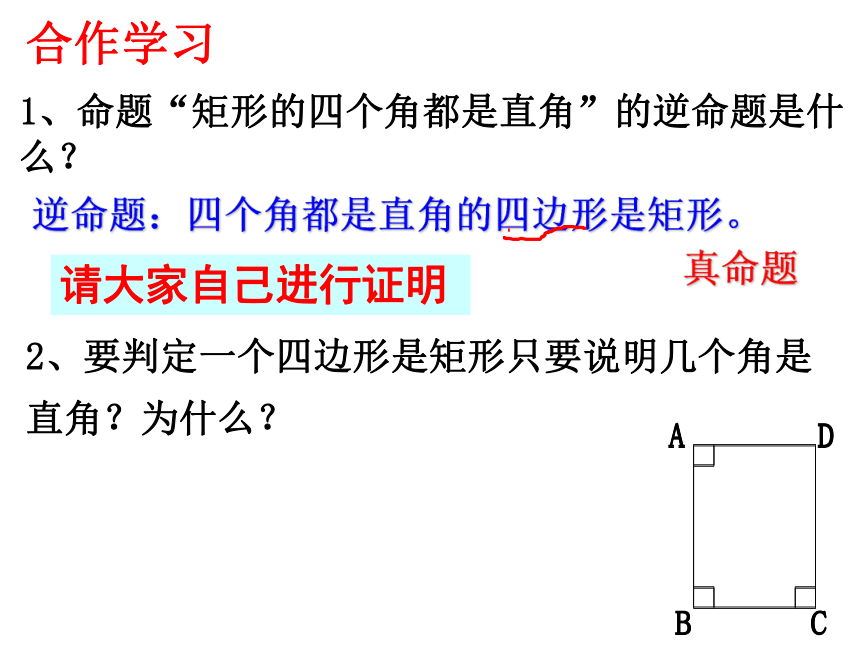
你知道这是为什么吗?有一个角是直角的平行四边形叫做矩形 你知道吗？矩形定义判定：1、命题“矩形的四个角都是直角”的逆命题是什么？合作学习请大家自己进行证明逆命题：四个角都是直角的四边形是矩形。真命题判定定理1：有三个角是直角的四边形是矩形.几何语言： ∵∠A=∠B=∠C=90°，
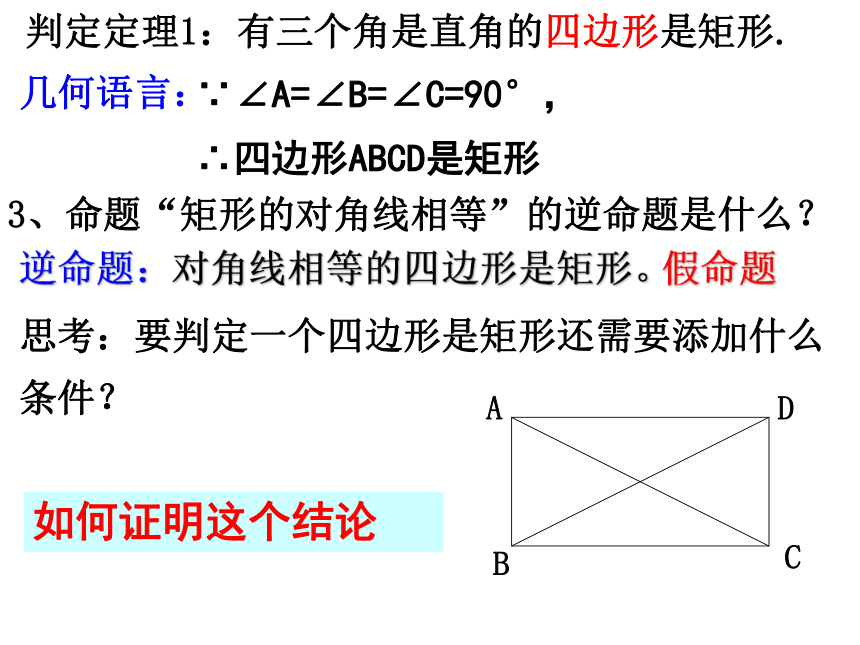
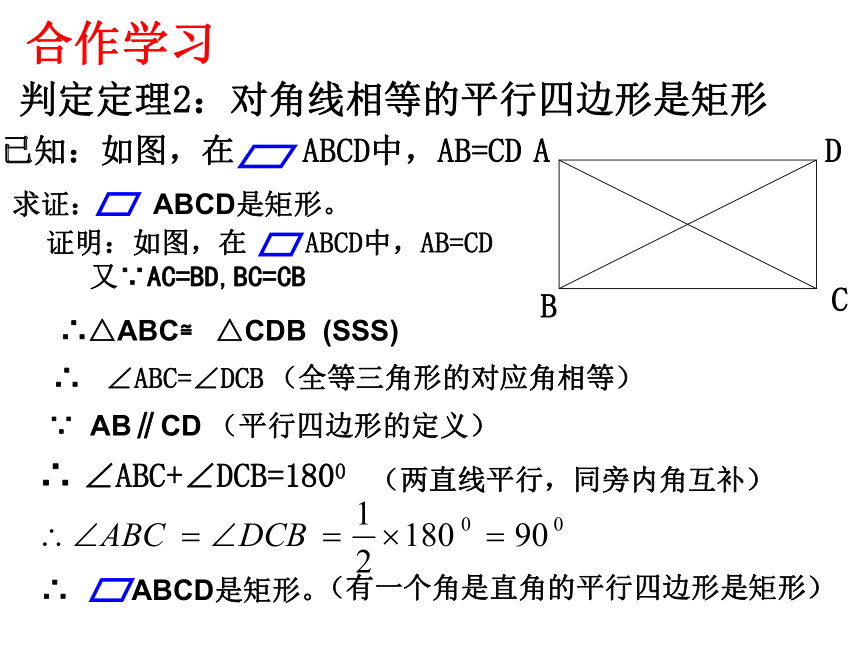
∴四边形ABCD是矩形3、命题“矩形的对角线相等”的逆命题是什么？逆命题：对角线相等的四边形是矩形。假命题思考：要判定一个四边形是矩形还需要添加什么条件？如何证明这个结论判定定理2：对角线相等的平行四边形是矩形合作学习已知：如图，在 ABCD中，AB=CD求证： ABCD是矩形。 证明：如图，在 ABCD中，AB=CD
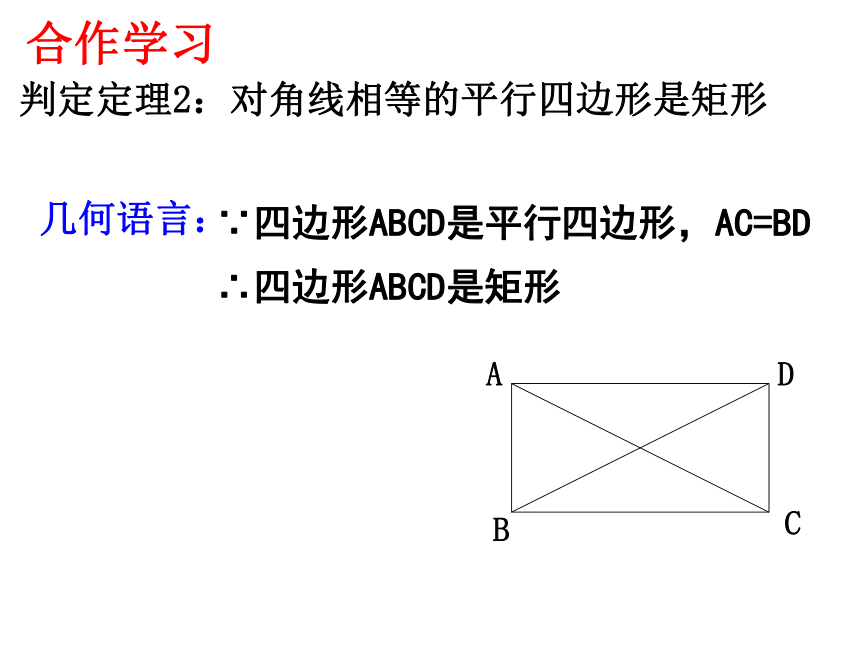
又∵AC=BD,BC=CB∴ ∠ABC+∠DCB=1800∴△ABC≌ △CDB (SSS)∴ ∠ABC=∠DCB（全等三角形的对应角相等） ∵ AB∥CD （平行四边形的定义）（两直线平行，同旁内角互补） ∴ ABCD是矩形。 （有一个角是直角的平行四边形是矩形）判定定理2：对角线相等的平行四边形是矩形几何语言： ∵四边形ABCD是平行四边形，AC=BD
∴四边形ABCD是矩形合作学习［问题］一张四边形纸板ＡＢＣＤ形状如图，
（１)若要从这张纸板中剪出一个平行四边形，并且使它的四个顶点分别落在四边形ＡＢＣＤ的四条边上，可怎样剪？ＥＦＧＨ⑵四边形ＡＢＣＤ满足什么情况下中点四边形ＥＦＧＨ为矩形？并说明理由．两条对角线互相垂直，ＡＣ⊥ＢＤ解：如图，分别取AB.BC,CD,DA的中点E,F,G,H.依次连结EF,
FG,GH,HE。沿四边形EFGH的各条边剪，就能剪出符合要求的
平行四边形。理由如下：［问题］一张四边形纸板ＡＢＣＤ形状如图，ＥＦＧＨ⑵四边形ＡＢＣＤ满足什么情况下中点四边形ＥＦＧＨ为矩形？并说明理由．解：两条对角线互相垂直，ＡＣ⊥ＢＤ理由如下：∵EF是△ABC的一条中位线。∴EF∥AC（三角形的中位线平行且等于第三边的一半）又∵EH是△ABD的一条中位线。又∵ＡＣ⊥ＢＤ（已知）∴EF⊥ＢＤ∴EH∥BD∴EF⊥EH即∠HEF=Rt∠；∠EHG=Rt∠,∠HGF=Rt∠.四边形ＥＦＧＨ为矩形（有三个角是直角的四边形是矩形）矩形有几种判定方法？有一个角是直角的平行四边形叫做矩形（定义）
有三个角是直角的四边形是矩形（判定定理1）
对角线相等的平行四边形是矩形（判定定理2）矩形有一个角是直角对角线相等有三个角是直角方法总结：如图，AC，BD是矩形ABCD的两条对角线，AE=CG=BF=DH.
求证：四边形EFGH是矩形练一练证明：在矩形ABCD中，AO=BO=CO=DO（矩形ABCD的两条对角线相等且互相平分）∵ AE=CG=BF=DH（已知）.∴ OE=OF=OG=OH∴ EG, HF互相平分，四边形EFGH是平行四边形（两条对角线互相平分的四边形是平行四边形）又∵ EG= HF ∴ 四边形EFGH是矩形（两条对角线相等的平行四边形是矩形）。做一做1、已知：如图，Rt△ABC≌Rt△CDA，且AD的对应边是CB，∠B=∠D=Rt∠； 求证：四边形ABCD是矩形。ADCB证明：∵Rt△ABC≌Rt△CDA(已知)∴ ∠DCA=∠CAB
(全等三角形的对应角相等)∴∠DAC+∠DCA =900∵ ∠B=∠D=Rt∠(已知)；∴ ∠DAC+∠CAB =900∴四边形ABCD是矩形(有三个角是直角的四边形是矩形)　谈谈你的收获、感受？！拓展提升（作业题4）1.已知：如图，在四边形ABCD中，AB=AD，CB=CD，点M，N，P，Q分别是AB，BC，CD，DA的中点；
求证：四边形MNPQ是矩形。证明：∵ AB=AD，CB=CD，∴AC⊥BD.又∵M，N，P，Q分别是AB，BC，CD，DA的中点； (三角形的中位线平行且等于第三边的一半)∴四边形MNPQ是平行四边形(一组对边平行且相等的四边形是平行四边形 )∴PQ∥AC ∴∠DQP=∠DAC,∴∠DAC+∠ADB=900 ∠AQM+∠DQP=900∴QM∥BD∴∠AQM=DAB,而AC⊥BDer∴∠MQP=900,∴四边形MNPQ是矩形(矩形定义)拓展提升（作业题5）2.已知:如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个
无缝隙、无重叠的四边形EFGH.
(1)求证:四边形EFGH是矩形.
(2)若EH＝3 cm,EF＝4 cm,求边AD的长
:(1)提示:由题意可得EH 平分∠AHF,GH 平分∠DHF,由此可
得∠EHG＝Rt∠,同理可得∠HEF＝∠HGF＝Rt∠,
∴ 四边形EFGH 是矩形(有三个角是直角的四边形是矩形).
(2)由题意可得HF＝ =5.
∴ EJ＝GK＝,
由此可得HJ＝FK,HK＝FJ,
∴ AD＝AH+HD＝HJ+FJ＝HF＝5(cm).