5.2 菱形 (2) 课件(共22张PPT)
文档属性
| 名称 | 5.2 菱形 (2) 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-10 11:15:40 | ||
图片预览


文档简介
(共22张PPT)
浙教版八年级下册
5.2 菱形 (2)
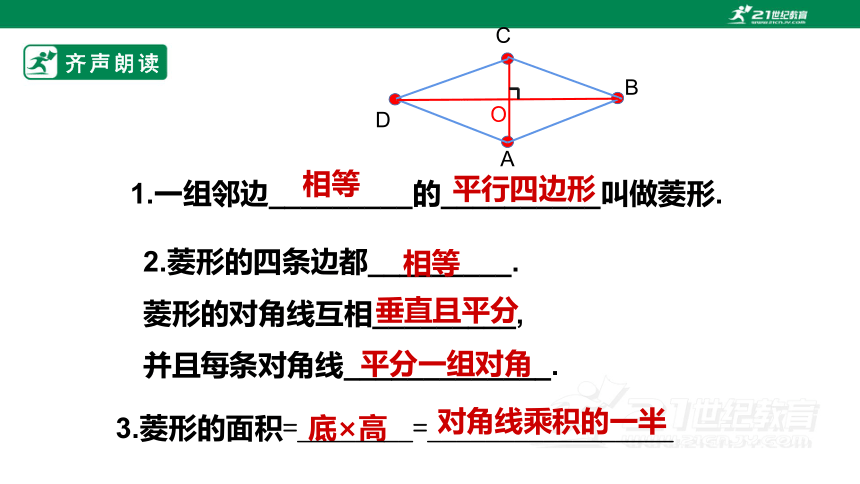
齐声朗读
1.一组邻边_________的__________叫做菱形.
相等
平行四边形
2.菱形的四条边都_________.
菱形的对角线互相_________,
并且每条对角线_____________.
相等
垂直且平分
平分一组对角
底×高
3.菱形的面积=________=_________________
对角线乘积的一半
A
C
D
B
O
新知导入
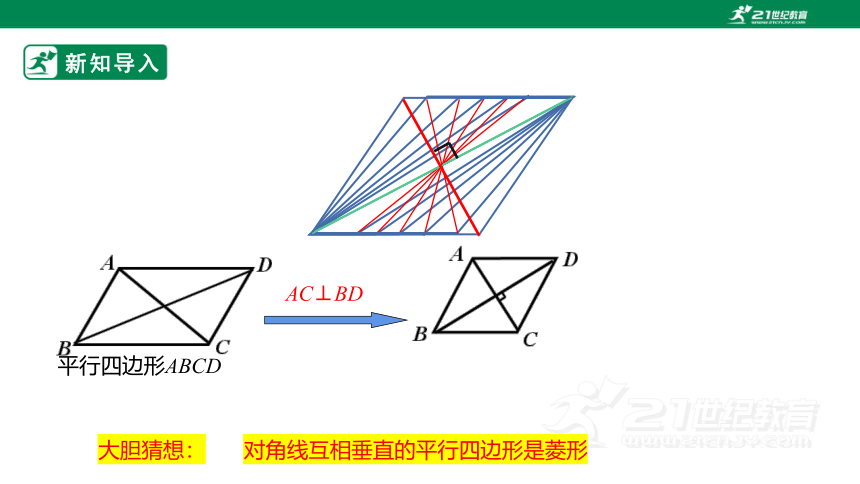
大胆猜想:
对角线互相垂直的平行四边形是菱形
平行四边形ABCD
AC⊥BD
新知导入
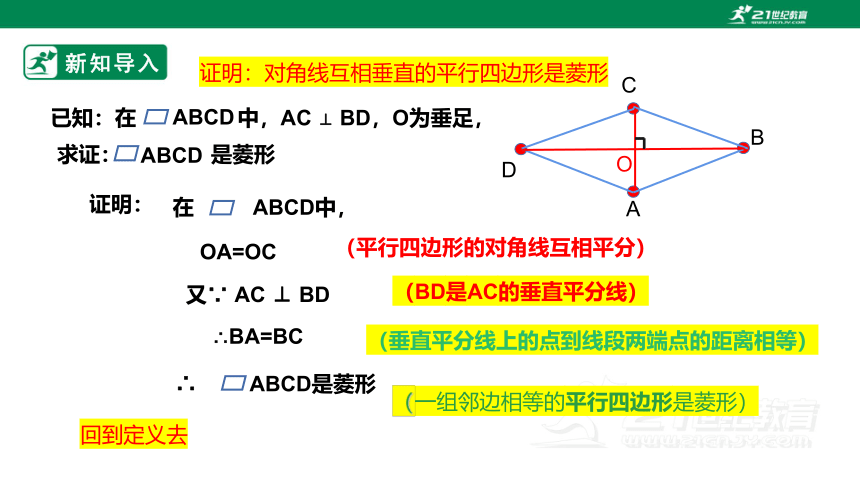
证明:对角线互相垂直的平行四边形是菱形
证明:
在 ABCD中,
OA=OC
又∵ AC ⊥ BD
A
C
D
B
O
∴BA=BC
(BD是AC的垂直平分线)
已知:在 中,AC ⊥ BD,O为垂足,
ABCD
ABCD
求证: 是菱形
∴ ABCD是菱形
(平行四边形的对角线互相平分)
(垂直平分线上的点到线段两端点的距离相等)
(一组邻边相等的平行四边形是菱形)
回到定义去
新知导入
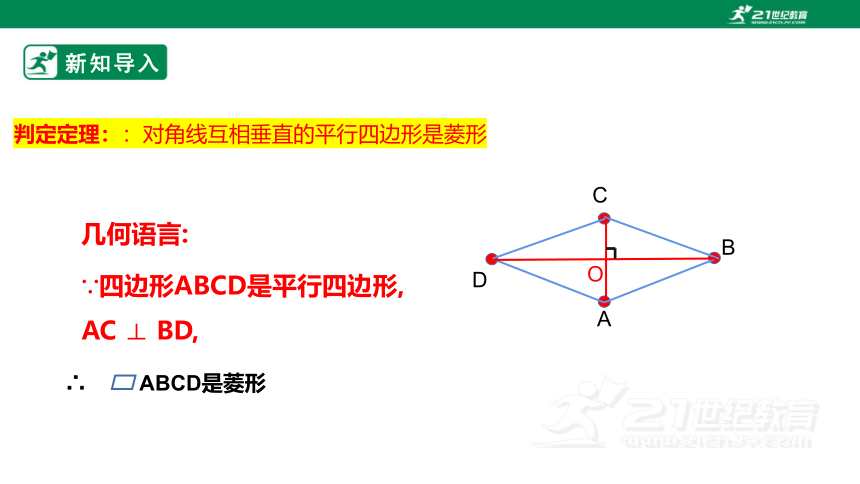
判定定理::对角线互相垂直的平行四边形是菱形
A
C
D
B
O
几何语言:
∵四边形ABCD是平行四边形,
AC ⊥ BD,
∴ ABCD是菱形
新知导入
新知导入
A
B
C
D
A
B
C
D
A
B
C
D
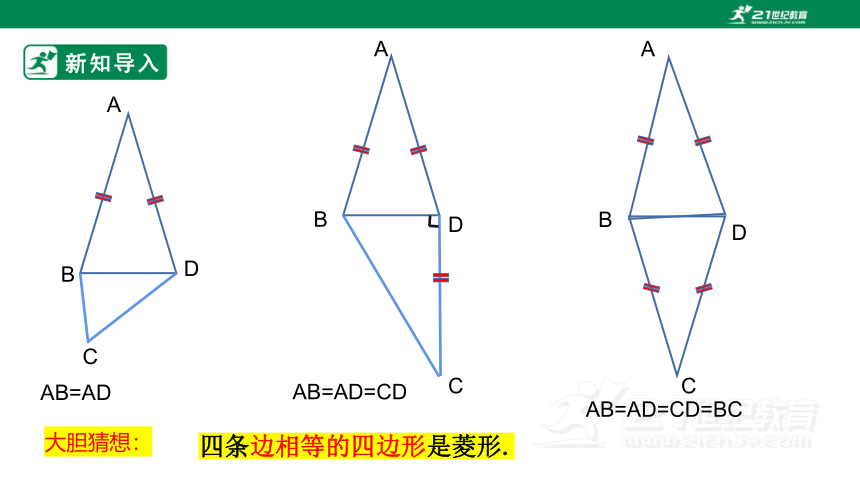
AB=AD
AB=AD=CD
AB=AD=CD=BC
大胆猜想:
四条边相等的四边形是菱形.
新知导入
证明:四条边相等的四边形的菱形
A
B
C
D
已知: 在四边形ABCD中,AB=BC=CD=DA,
求证:四边形ABCD是菱形
证明:∵AB=CD,BC=DA,
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形
回到定义去
新知导入
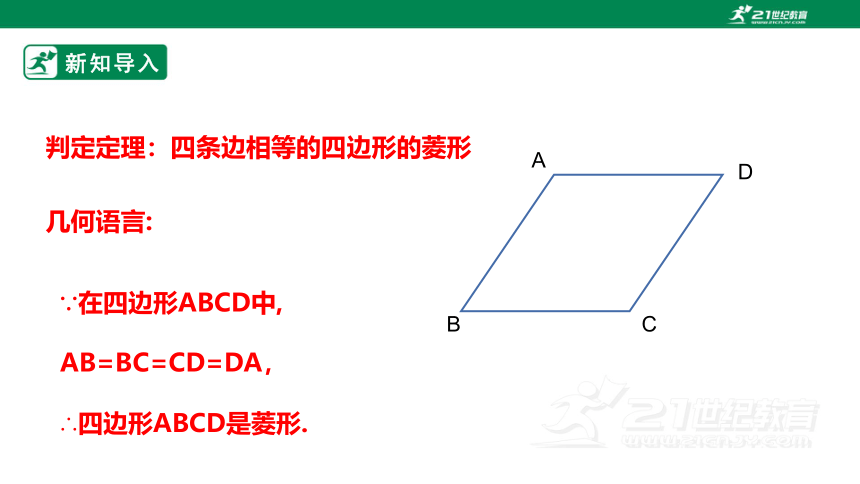
判定定理:四条边相等的四边形的菱形
几何语言:
A
B
C
D
∵在四边形ABCD中,
AB=BC=CD=DA,
∴四边形ABCD是菱形.
新知讲解
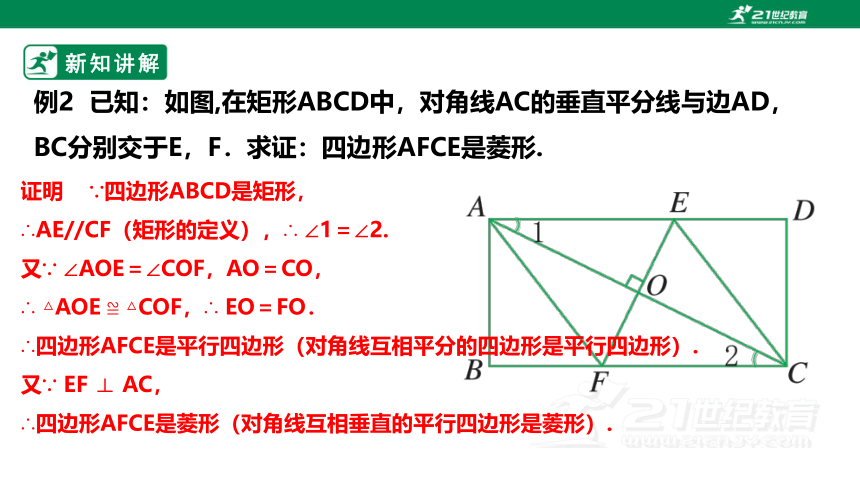
例2 已知:如图,在矩形ABCD中,对角线AC的垂直平分线与边AD,BC分别交于E,F.求证:四边形AFCE是菱形.
证明 ∵四边形ABCD是矩形,
∴AE//CF(矩形的定义),∴ ∠1=∠2.
又∵ ∠AOE=∠COF,AO=CO,
∴ △AOE ≌ △COF,∴ EO=FO.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形).
又∵ EF ⊥ AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
新知讲解
取一张长方形纸片,按下图的方法对折两次,并沿图(3)中的斜线(虚线)剪开,把剪下的①这部分展开,平铺在桌面上。
剪出的这个图形是一定是菱形吗,为什么?
1:四条边相等的四边形的菱形
2.对角线互相垂直的平行四边形是菱形
知识小结
菱形常用的判定方法:
1.有一组邻边相等的平行四边形叫做菱形.
2.四条边相等的四边形是菱形.
3.对角线互相垂直的平行四边形是菱形.
4.对角线互相垂直平分的四边形是菱形.
一分钟背诵
当堂检测
当堂检测
当堂检测
1.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
B
夯实基础,稳扎稳打
四条边相等的四边形是菱形.
2. 如图, ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.
A
B
C
D
O
证明:
∵ OA=4,OB=3,AB=5,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
即AC⊥BD,
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形)
3.如图,在△ABC中,AB=AC,△ABC经过怎样的运动,所得图形与△ABC组成一个菱形?叙述图形的运动过程,并作出所得的图形。
A
B
C
A
'
A
B
C
A
B
C
以BC边所在直线为对称轴,作轴对称变换
以BC边中点O为旋转中心,作中心对称变换
O
连续递推,豁然开朗
4.如图,将一张矩形纸片对折剪开,得到两张长、宽一样大小的矩形纸条,
将其叠放得到重叠部分四边形ABCD.求证:四边形ABCD是菱形.
证明:过点A作AE⊥BC于E,AF⊥CD于F
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵两条纸条宽度相同
∴AE=AF
E
F
面积算两次
课堂练习
5.已知:如图,O是矩形ABCD的对角线的交点。作DE∥AC,CE∥BD,DE,CE相交于点E。 求证:四边形OECD是菱形
A
B
C
D
O
E
证明:
∵DE∥AC,CE∥BD
∴四边形OECD是平行四边形
在矩形ABCD中,
OD=0C
∴四边形OECD是菱形
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
6. 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
EF=GH= BD, FG=EH= AC
.
当堂检测
(3)在什么条件下,围成的四边形是矩形?
必定是平行四边形
△ ABC为等腰三角形,且AB=BC
.
C四边形BEFD=AB+BC
.
7.如图, DF , EF 是△ ABC 的两条中位线.我们探究的问题是:这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的边或角有什么关系.建议按下列步骤探索:
(1)围成的四边形是否必定是平行四边形?
(2)在什么条件下,围成的四边形是菱形?
(4)你还能发现其他什么结论吗?
8.在直角坐标系中,四边形ABCD的顶点A、B、C、D的坐标依次为
(-1,0),(x,y), (-1,5), (-7,z). 求x、y、z的值,使得四边形ABCD是菱形
x
y
O
在平面直角坐标系中,横坐标相同的点所在直线平行于y轴,
纵坐标相同的点所在直线平行于x轴,
A
C
D
B
M
中点平均数-----数形结合
9.如图,已知AD平分∠BAC,DE//AC,DF//AB.
求证:四边形AEDF是菱形
A
B
C
F
D
E
解(1):∵DE//AC,DF//AB
∴四边形AEDF是平行四边形
∵AD平分∠BAC,
∴∠1= ∠2
∵DE//AC,
∴∠3= ∠2,
∴∠1= ∠3,
∴ED=EA
∴四边形AEDF是菱形(一组邻边相等的平行四边形是菱形)
1
2
3
双平出等腰
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版八年级下册
5.2 菱形 (2)
齐声朗读
1.一组邻边_________的__________叫做菱形.
相等
平行四边形
2.菱形的四条边都_________.
菱形的对角线互相_________,
并且每条对角线_____________.
相等
垂直且平分
平分一组对角
底×高
3.菱形的面积=________=_________________
对角线乘积的一半
A
C
D
B
O
新知导入
大胆猜想:
对角线互相垂直的平行四边形是菱形
平行四边形ABCD
AC⊥BD
新知导入
证明:对角线互相垂直的平行四边形是菱形
证明:
在 ABCD中,
OA=OC
又∵ AC ⊥ BD
A
C
D
B
O
∴BA=BC
(BD是AC的垂直平分线)
已知:在 中,AC ⊥ BD,O为垂足,
ABCD
ABCD
求证: 是菱形
∴ ABCD是菱形
(平行四边形的对角线互相平分)
(垂直平分线上的点到线段两端点的距离相等)
(一组邻边相等的平行四边形是菱形)
回到定义去
新知导入
判定定理::对角线互相垂直的平行四边形是菱形
A
C
D
B
O
几何语言:
∵四边形ABCD是平行四边形,
AC ⊥ BD,
∴ ABCD是菱形
新知导入
新知导入
A
B
C
D
A
B
C
D
A
B
C
D
AB=AD
AB=AD=CD
AB=AD=CD=BC
大胆猜想:
四条边相等的四边形是菱形.
新知导入
证明:四条边相等的四边形的菱形
A
B
C
D
已知: 在四边形ABCD中,AB=BC=CD=DA,
求证:四边形ABCD是菱形
证明:∵AB=CD,BC=DA,
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形
回到定义去
新知导入
判定定理:四条边相等的四边形的菱形
几何语言:
A
B
C
D
∵在四边形ABCD中,
AB=BC=CD=DA,
∴四边形ABCD是菱形.
新知讲解
例2 已知:如图,在矩形ABCD中,对角线AC的垂直平分线与边AD,BC分别交于E,F.求证:四边形AFCE是菱形.
证明 ∵四边形ABCD是矩形,
∴AE//CF(矩形的定义),∴ ∠1=∠2.
又∵ ∠AOE=∠COF,AO=CO,
∴ △AOE ≌ △COF,∴ EO=FO.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形).
又∵ EF ⊥ AC,
∴四边形AFCE是菱形(对角线互相垂直的平行四边形是菱形).
新知讲解
取一张长方形纸片,按下图的方法对折两次,并沿图(3)中的斜线(虚线)剪开,把剪下的①这部分展开,平铺在桌面上。
剪出的这个图形是一定是菱形吗,为什么?
1:四条边相等的四边形的菱形
2.对角线互相垂直的平行四边形是菱形
知识小结
菱形常用的判定方法:
1.有一组邻边相等的平行四边形叫做菱形.
2.四条边相等的四边形是菱形.
3.对角线互相垂直的平行四边形是菱形.
4.对角线互相垂直平分的四边形是菱形.
一分钟背诵
当堂检测
当堂检测
当堂检测
1.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
B
夯实基础,稳扎稳打
四条边相等的四边形是菱形.
2. 如图, ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证:四边形ABCD是菱形.
A
B
C
D
O
证明:
∵ OA=4,OB=3,AB=5,
∴ AB2=OA2+OB2,
∴△AOB是直角三角形,
即AC⊥BD,
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形(对角线互相垂直的平行四边形是菱形)
3.如图,在△ABC中,AB=AC,△ABC经过怎样的运动,所得图形与△ABC组成一个菱形?叙述图形的运动过程,并作出所得的图形。
A
B
C
A
'
A
B
C
A
B
C
以BC边所在直线为对称轴,作轴对称变换
以BC边中点O为旋转中心,作中心对称变换
O
连续递推,豁然开朗
4.如图,将一张矩形纸片对折剪开,得到两张长、宽一样大小的矩形纸条,
将其叠放得到重叠部分四边形ABCD.求证:四边形ABCD是菱形.
证明:过点A作AE⊥BC于E,AF⊥CD于F
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵两条纸条宽度相同
∴AE=AF
E
F
面积算两次
课堂练习
5.已知:如图,O是矩形ABCD的对角线的交点。作DE∥AC,CE∥BD,DE,CE相交于点E。 求证:四边形OECD是菱形
A
B
C
D
O
E
证明:
∵DE∥AC,CE∥BD
∴四边形OECD是平行四边形
在矩形ABCD中,
OD=0C
∴四边形OECD是菱形
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
6. 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
EF=GH= BD, FG=EH= AC
.
当堂检测
(3)在什么条件下,围成的四边形是矩形?
必定是平行四边形
△ ABC为等腰三角形,且AB=BC
.
C四边形BEFD=AB+BC
.
7.如图, DF , EF 是△ ABC 的两条中位线.我们探究的问题是:这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的边或角有什么关系.建议按下列步骤探索:
(1)围成的四边形是否必定是平行四边形?
(2)在什么条件下,围成的四边形是菱形?
(4)你还能发现其他什么结论吗?
8.在直角坐标系中,四边形ABCD的顶点A、B、C、D的坐标依次为
(-1,0),(x,y), (-1,5), (-7,z). 求x、y、z的值,使得四边形ABCD是菱形
x
y
O
在平面直角坐标系中,横坐标相同的点所在直线平行于y轴,
纵坐标相同的点所在直线平行于x轴,
A
C
D
B
M
中点平均数-----数形结合
9.如图,已知AD平分∠BAC,DE//AC,DF//AB.
求证:四边形AEDF是菱形
A
B
C
F
D
E
解(1):∵DE//AC,DF//AB
∴四边形AEDF是平行四边形
∵AD平分∠BAC,
∴∠1= ∠2
∵DE//AC,
∴∠3= ∠2,
∴∠1= ∠3,
∴ED=EA
∴四边形AEDF是菱形(一组邻边相等的平行四边形是菱形)
1
2
3
双平出等腰
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
