5.3 正方形(1) 课件(共22张PPT)
文档属性
| 名称 | 5.3 正方形(1) 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-11 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
浙教版八年级下册
5.3 正方形 (1)
新知导入
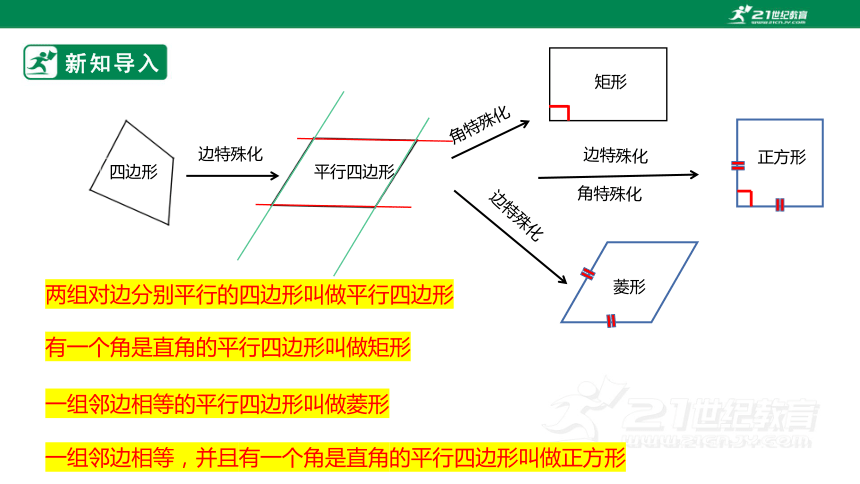
四边形
边特殊化
角特殊化
两组对边分别平行的四边形叫做平行四边形
有一个角是直角的平行四边形叫做矩形
平行四边形
矩形
边特殊化
一组邻边相等的平行四边形叫做菱形
菱形
角特殊化
边特殊化
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
正方形
新知导入
新知导入
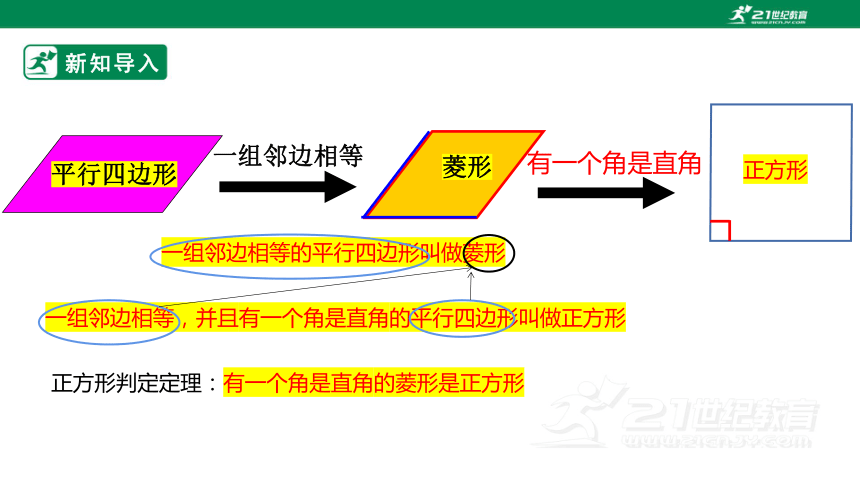
一组邻边相等的平行四边形叫做菱形
平行四边形
一组邻边相等
菱形
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
有一个角是直角
正方形判定定理:有一个角是直角的菱形是正方形
正方形
新知导入
有一个角是直角的平行四边形叫做矩形。
平行四边形
矩形
有一个角
是直角
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
一组邻边相等
正方形
正方形判定定理:一组邻边相等的矩形是正方形
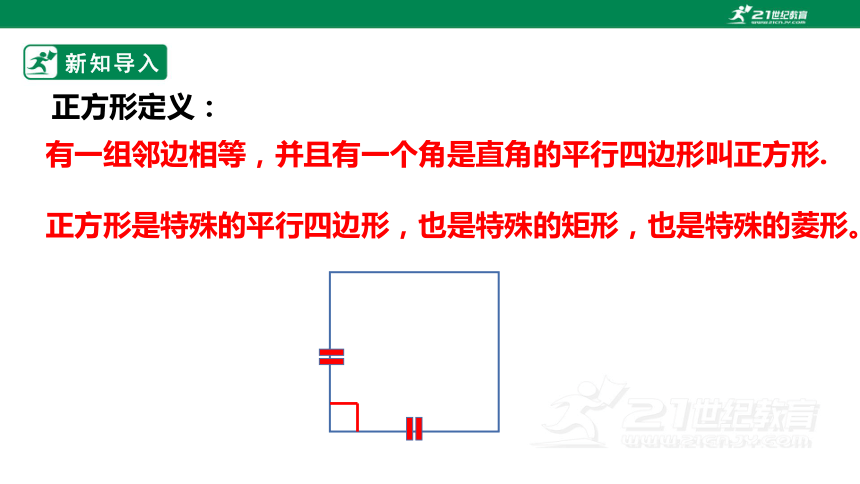
正方形定义:
有一组邻边相等,并且有一个角是直角的平行四边形叫正方形.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
新知导入
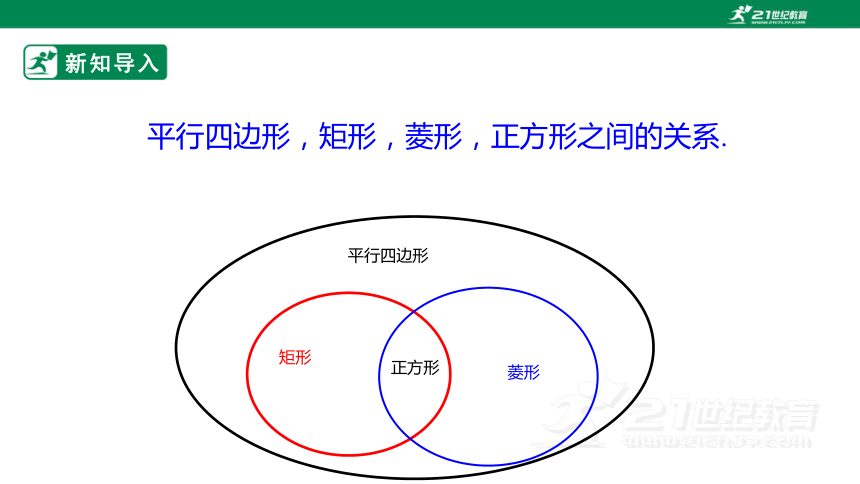
平行四边形,矩形,菱形,正方形之间的关系.
平行四边形
矩形
菱形
正方形
新知导入
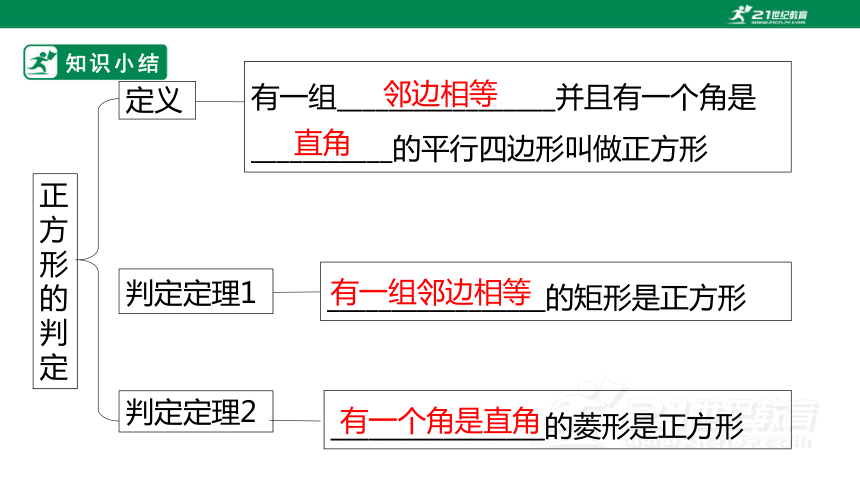
正方形的判定
定义
判定定理2
判定定理1
有一组_________________并且有一个角是___________的平行四边形叫做正方形
_________________的矩形是正方形
_________________的菱形是正方形
邻边相等
直角
有一组邻边相等
有一个角是直角
知识小结
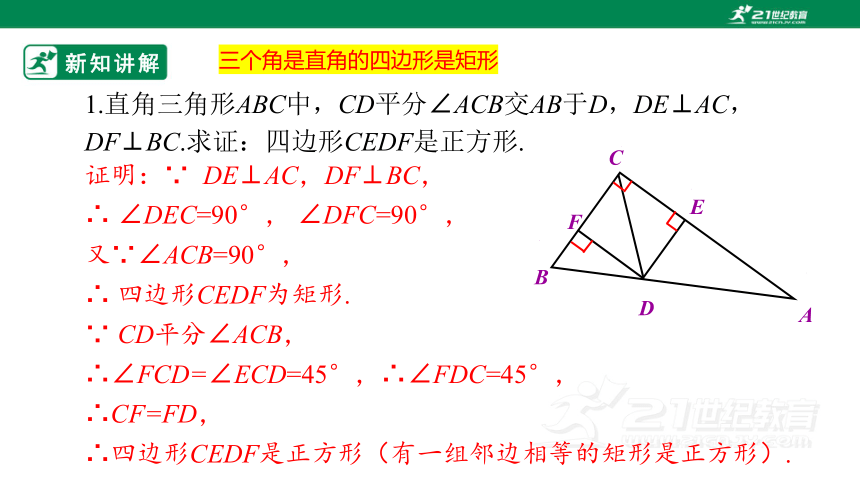
1.直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥BC.求证:四边形CEDF是正方形.
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
∴∠FCD=∠ECD=45°,∴∠FDC=45°,
∵ CD平分∠ACB,
∴ 四边形CEDF为矩形.
又∵∠ACB=90°,
∴ ∠DEC=90°, ∠DFC=90°,
证明:∵ DE⊥AC,DF⊥BC,
∴CF=FD,
A
B
C
D
E
F
C
D
E
A
B
新知讲解
三个角是直角的四边形是矩形
新知讲解
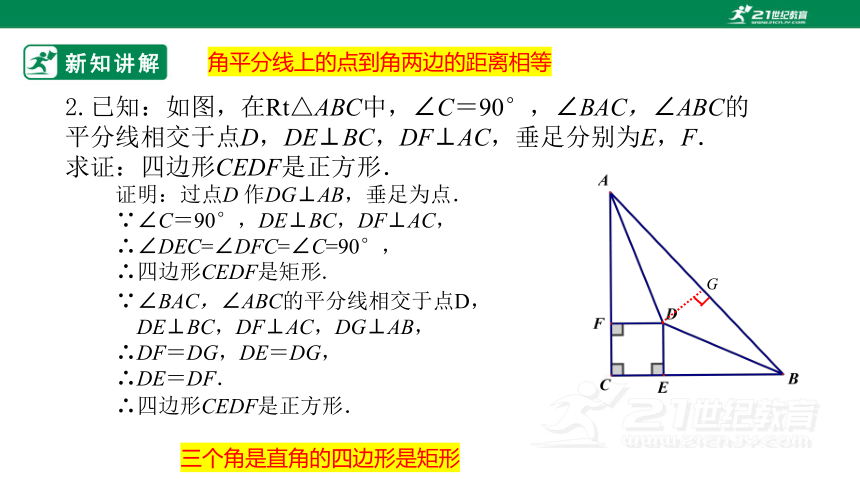
2.已知:如图,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的
平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E,F.
求证:四边形CEDF是正方形.
G
证明:过点D 作DG⊥AB,垂足为点.
∵∠C=90°,DE⊥BC,DF⊥AC,
∴∠DEC=∠DFC=∠C=90°,
∴四边形CEDF是矩形.
∵∠BAC,∠ABC的平分线相交于点D,
DE⊥BC,DF⊥AC,DG⊥AB,
∴DF=DG,DE=DG,
∴DE=DF.
∴四边形CEDF是正方形.
角平分线上的点到角两边的距离相等
三个角是直角的四边形是矩形
夯实基础,稳扎稳打
1.判断对错:
(1)对角线互相垂直,一个角是直角的四边形是正方形( )
(2)如果一个菱形的对角线相等,那么它一定是正方形 ( )
(3)如果一个矩形的对角线互相垂直,那么它一定是正方形 ( )
(4)四条边相等,且有一个角是直角的四边形是正方形( )
×
√
√
√
课堂练习
2.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
D
A
B
C
D
课堂练习
3.如图,矩形ABCD中,对角线AC与BD互相垂直.
求证:矩形ABCD是正方形.
A
D
C
B
O
证明:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,
又∵AC⊥BD.
∴∠AOD=∠AOB=90°,
在△AOB和△AOD中,
OB=OD,∠AOB=∠AOD,OA=OA,
∴△AOB≌△AOD,∴AB=AD.
∴矩形ABCD是正方形.
课堂练习
矩形+一组邻边相等=正方形
4.在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.
求证:四边形EFMN是正方形
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,∴AN=BE=CF=DM.
课堂练习
菱形+有一个角是直角=正方形
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,∠A=∠B=∠C=∠D, AN=BE=CF=DM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)=180°-90°=90°.
∴四边形EFMN是正方形 .
∴△AEN ≌△BFE≌△CMF≌△DNM,
5.判断命题“对角线互相垂直且相等的四边形是正方形”是否成立。
如果不成立,请增加一个条件使它成立
A
B
C
D
AC⊥BD, AC=BD
增加条件:对角线互相平分
A
B
C
D
O
判定定理:对角线互相垂直平分且相等的四边形是正方形
课堂练习
对角线:垂直+平分+相等=正方形
还原-----恢复原状
C
6.
课堂练习
连续递推,豁然开朗
课堂练习
7.求证:矩形的各内角平分线围成的四边形是正方形
A
B
C
D
E
F
G
H
已知:在矩形ABCD中,
AE、BG、CG、DE分别平分
∠BAD、∠ABC、∠BCD、∠CDA
求证:四边形EFGH是正方形
分析:
450
450
450
450
450
450
第一个等腰Rt△ABH
450
450
第二个等腰Rt△BCG
第三个等腰Rt△DCF
第四个等腰Rt△ADE
△ABH ≌△DCF
AE-AH=DE-DF
EH=EF
一组邻边相等的矩形是正方形
7.求证:矩形的各内角平分线围成的四边形是正方形
课堂练习
8.在直角坐标系中,点A,B,C,D的坐标依次为(-a,-b),(a,-b),(a,b),(-a,b).
要使四边形ABCD为正方形,a,b的值必须满足什么条件
x
y
O
A
B
C
D
在直角坐标系中,点A(x,y)与点B(-x,-y)关于原点成中心对称
a
b
=
课堂练习
(a≠0,b≠0)
9.已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
证明:∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴∠ABC=90°,∠DCB=90°.
又∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ABC=45°,∠ECB=∠DCB=45°.
∴∠EBC=∠ECB.∴EB=EC.
课堂练习
∴ BECF是菱形(菱形的定义).
在△EBC中,∵∠EBC=45°,∠ECB=45°,
∴∠BEC=90°.
∴菱形BECF是正方形(有一个角是直角的菱形是正方形).
新知讲解
证明: ∵四边形ABCD是矩形
∴∠B=∠D=∠C=90
∵△AEF是等边三角形
∴AE=AF,∠AEF=∠AFE=60
∵∠CEF=45 ∴∠CFE=45
∴∠AFD=∠AEB=180 -45 -60 = 75
∴矩形ABCD是正方形
∴△AEB≌△AFD,AB=AD
C
B
D
A
E
F
10. 如图,等边三角形AEF的顶点为E,F在矩形ABCD的边BC、CD上,且∠CEF=45 . 求证:矩形ABCD是正方形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版八年级下册
5.3 正方形 (1)
新知导入
四边形
边特殊化
角特殊化
两组对边分别平行的四边形叫做平行四边形
有一个角是直角的平行四边形叫做矩形
平行四边形
矩形
边特殊化
一组邻边相等的平行四边形叫做菱形
菱形
角特殊化
边特殊化
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
正方形
新知导入
新知导入
一组邻边相等的平行四边形叫做菱形
平行四边形
一组邻边相等
菱形
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
有一个角是直角
正方形判定定理:有一个角是直角的菱形是正方形
正方形
新知导入
有一个角是直角的平行四边形叫做矩形。
平行四边形
矩形
有一个角
是直角
一组邻边相等,并且有一个角是直角的平行四边形叫做正方形
一组邻边相等
正方形
正方形判定定理:一组邻边相等的矩形是正方形
正方形定义:
有一组邻边相等,并且有一个角是直角的平行四边形叫正方形.
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
新知导入
平行四边形,矩形,菱形,正方形之间的关系.
平行四边形
矩形
菱形
正方形
新知导入
正方形的判定
定义
判定定理2
判定定理1
有一组_________________并且有一个角是___________的平行四边形叫做正方形
_________________的矩形是正方形
_________________的菱形是正方形
邻边相等
直角
有一组邻边相等
有一个角是直角
知识小结
1.直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥BC.求证:四边形CEDF是正方形.
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
∴∠FCD=∠ECD=45°,∴∠FDC=45°,
∵ CD平分∠ACB,
∴ 四边形CEDF为矩形.
又∵∠ACB=90°,
∴ ∠DEC=90°, ∠DFC=90°,
证明:∵ DE⊥AC,DF⊥BC,
∴CF=FD,
A
B
C
D
E
F
C
D
E
A
B
新知讲解
三个角是直角的四边形是矩形
新知讲解
2.已知:如图,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的
平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E,F.
求证:四边形CEDF是正方形.
G
证明:过点D 作DG⊥AB,垂足为点.
∵∠C=90°,DE⊥BC,DF⊥AC,
∴∠DEC=∠DFC=∠C=90°,
∴四边形CEDF是矩形.
∵∠BAC,∠ABC的平分线相交于点D,
DE⊥BC,DF⊥AC,DG⊥AB,
∴DF=DG,DE=DG,
∴DE=DF.
∴四边形CEDF是正方形.
角平分线上的点到角两边的距离相等
三个角是直角的四边形是矩形
夯实基础,稳扎稳打
1.判断对错:
(1)对角线互相垂直,一个角是直角的四边形是正方形( )
(2)如果一个菱形的对角线相等,那么它一定是正方形 ( )
(3)如果一个矩形的对角线互相垂直,那么它一定是正方形 ( )
(4)四条边相等,且有一个角是直角的四边形是正方形( )
×
√
√
√
课堂练习
2.已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
D
A
B
C
D
课堂练习
3.如图,矩形ABCD中,对角线AC与BD互相垂直.
求证:矩形ABCD是正方形.
A
D
C
B
O
证明:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,
又∵AC⊥BD.
∴∠AOD=∠AOB=90°,
在△AOB和△AOD中,
OB=OD,∠AOB=∠AOD,OA=OA,
∴△AOB≌△AOD,∴AB=AD.
∴矩形ABCD是正方形.
课堂练习
矩形+一组邻边相等=正方形
4.在正方形ABCD中,点E、F、M、N分别在各边上,且AE=BF=CM=DN.
求证:四边形EFMN是正方形
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,∴AN=BE=CF=DM.
课堂练习
菱形+有一个角是直角=正方形
在△AEN、△BFE、△CMF、△DNM中,
AE=BF=CM=DN,∠A=∠B=∠C=∠D, AN=BE=CF=DM,
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)=180°-90°=90°.
∴四边形EFMN是正方形 .
∴△AEN ≌△BFE≌△CMF≌△DNM,
5.判断命题“对角线互相垂直且相等的四边形是正方形”是否成立。
如果不成立,请增加一个条件使它成立
A
B
C
D
AC⊥BD, AC=BD
增加条件:对角线互相平分
A
B
C
D
O
判定定理:对角线互相垂直平分且相等的四边形是正方形
课堂练习
对角线:垂直+平分+相等=正方形
还原-----恢复原状
C
6.
课堂练习
连续递推,豁然开朗
课堂练习
7.求证:矩形的各内角平分线围成的四边形是正方形
A
B
C
D
E
F
G
H
已知:在矩形ABCD中,
AE、BG、CG、DE分别平分
∠BAD、∠ABC、∠BCD、∠CDA
求证:四边形EFGH是正方形
分析:
450
450
450
450
450
450
第一个等腰Rt△ABH
450
450
第二个等腰Rt△BCG
第三个等腰Rt△DCF
第四个等腰Rt△ADE
△ABH ≌△DCF
AE-AH=DE-DF
EH=EF
一组邻边相等的矩形是正方形
7.求证:矩形的各内角平分线围成的四边形是正方形
课堂练习
8.在直角坐标系中,点A,B,C,D的坐标依次为(-a,-b),(a,-b),(a,b),(-a,b).
要使四边形ABCD为正方形,a,b的值必须满足什么条件
x
y
O
A
B
C
D
在直角坐标系中,点A(x,y)与点B(-x,-y)关于原点成中心对称
a
b
=
课堂练习
(a≠0,b≠0)
9.已知:如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
证明:∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴∠ABC=90°,∠DCB=90°.
又∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ABC=45°,∠ECB=∠DCB=45°.
∴∠EBC=∠ECB.∴EB=EC.
课堂练习
∴ BECF是菱形(菱形的定义).
在△EBC中,∵∠EBC=45°,∠ECB=45°,
∴∠BEC=90°.
∴菱形BECF是正方形(有一个角是直角的菱形是正方形).
新知讲解
证明: ∵四边形ABCD是矩形
∴∠B=∠D=∠C=90
∵△AEF是等边三角形
∴AE=AF,∠AEF=∠AFE=60
∵∠CEF=45 ∴∠CFE=45
∴∠AFD=∠AEB=180 -45 -60 = 75
∴矩形ABCD是正方形
∴△AEB≌△AFD,AB=AD
C
B
D
A
E
F
10. 如图,等边三角形AEF的顶点为E,F在矩形ABCD的边BC、CD上,且∠CEF=45 . 求证:矩形ABCD是正方形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
