2.4 二次函数的应用(1)(浙江省温州市平阳县)
文档属性
| 名称 | 2.4 二次函数的应用(1)(浙江省温州市平阳县) |

|
|
| 格式 | rar | ||
| 文件大小 | 198.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-16 00:00:00 | ||
图片预览





文档简介
课件13张PPT。2.4 二次函数的应用⑴浙教版九年级上册第二章二次函数 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.(1)若商场平均每天要盈利1200元,每件衬衫应降价
多少元?提出问题 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.(2)问每件衬衫降价多少元时,商场平均每天盈利最多?最多为多少元?提出问题想一想:如果我们把平均每天盈利与降价的函数关系找出来,
那么所求问题就转化为什么问题?1.发现可以设降价为x元,每天盈利为y元,则y关于x
的函数关系式为y=(40-x)(20+2x),化为
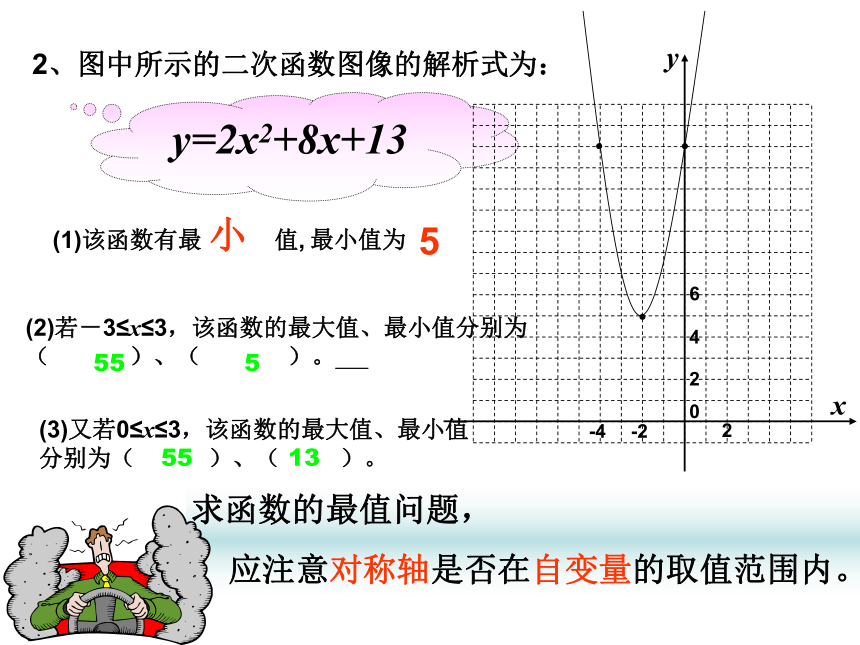
这是一个二次函数.2.写出自变量x的取值范围,再求出它的最大值.2、图中所示的二次函数图像的解析式为:
y=2x2+8x+13(2)若-3≤x≤3,该函数的最大值、最小值分别为( )、( )。 (3)又若0≤x≤3,该函数的最大值、最小值分别为( )、( )。求函数的最值问题,
应注意对称轴是否在自变量的取值范围内。55 555 13(1)该函数有最 值,小最小值为5探究实践用长6米铝合金条制成如图形状的矩形窗框,
问长和高各是多少米时,窗户的透光面积
最大?最大面积是多少?(1)设什么为自变量x?(窗框的长或高)(2)如果学生设窗框长为x,则高为多少?面积为多少?(3)若设透光面积为y,试写出y关于x的函数解析式(4)这里自变量x的取值范围是什么?根据什么来确定?用长6米铝合金条制成如图形状的矩形窗框,问长和高各是多少米时,窗户的透光面积最大?最大面积是多少?x解:设窗框长为x,则它的高为 ,再设透光面积为y,由题意得:答:当长为1米,宽为 米时,窗户的透光面积最大,最大面积是 平方米最值问题的一般步骤(1)列出二次函数的解析式.列解析式时,要根据自变量
的实际意义,确定自变量的取值范围.(2)在自变量的取值范围内,运用公式或配方法求出二次函数的最大值或最小值.探究与建模3.图中窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形.如果制作一个窗户边框的材料的总长度为8米,那么如何设计这个窗户边框的尺寸,使透光面积最大?(结果精确到0.01米)解:设半圆的半径为r米,如图,矩形的一边长为l米,根据题意,有:5r+πr+2r+2l=8,即:l=4-0.5(π+7)r又因为:l>0且r >0所以: 4-0.5(π+7)r>0则:0<r<(0<r< )变式与拓展如图,隧道横截面的下部是矩形,上部是半圆,周长为16米。
⑴求截面积S(米2)关于底部宽x(米)的函数解析式,及自变量x 的取值范围?
⑵试问:当底部宽x为几米时,隧道的截面积S最大(结果精确到0.01米)?解:∵隧道的底部宽为x,周长为16,答:当隧道的底部宽度为4.48米时,隧道的截面积最大。练一练 ( 1)已知直角三角形的两直角边的和为2。求斜
边长可能达到的最小值,以及当斜边长达到最
小值时两条直角边的长分别为多少?解:设其中一条直角边长为x,则另一条为(2-x),设斜边长为y,由勾股定理得,课堂小结本节课主要讲了将实际问题转化为数学模型.
运用二次函数求实际问题中的最大值或最小值,首先应求出函数解析式和自变量的取值范围,然后通过配方变形,或利用公式求她的最大值或最小值.值得注意的是,由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
多少元?提出问题 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.(2)问每件衬衫降价多少元时,商场平均每天盈利最多?最多为多少元?提出问题想一想:如果我们把平均每天盈利与降价的函数关系找出来,
那么所求问题就转化为什么问题?1.发现可以设降价为x元,每天盈利为y元,则y关于x
的函数关系式为y=(40-x)(20+2x),化为
这是一个二次函数.2.写出自变量x的取值范围,再求出它的最大值.2、图中所示的二次函数图像的解析式为:
y=2x2+8x+13(2)若-3≤x≤3,该函数的最大值、最小值分别为( )、( )。 (3)又若0≤x≤3,该函数的最大值、最小值分别为( )、( )。求函数的最值问题,
应注意对称轴是否在自变量的取值范围内。55 555 13(1)该函数有最 值,小最小值为5探究实践用长6米铝合金条制成如图形状的矩形窗框,
问长和高各是多少米时,窗户的透光面积
最大?最大面积是多少?(1)设什么为自变量x?(窗框的长或高)(2)如果学生设窗框长为x,则高为多少?面积为多少?(3)若设透光面积为y,试写出y关于x的函数解析式(4)这里自变量x的取值范围是什么?根据什么来确定?用长6米铝合金条制成如图形状的矩形窗框,问长和高各是多少米时,窗户的透光面积最大?最大面积是多少?x解:设窗框长为x,则它的高为 ,再设透光面积为y,由题意得:答:当长为1米,宽为 米时,窗户的透光面积最大,最大面积是 平方米最值问题的一般步骤(1)列出二次函数的解析式.列解析式时,要根据自变量
的实际意义,确定自变量的取值范围.(2)在自变量的取值范围内,运用公式或配方法求出二次函数的最大值或最小值.探究与建模3.图中窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形.如果制作一个窗户边框的材料的总长度为8米,那么如何设计这个窗户边框的尺寸,使透光面积最大?(结果精确到0.01米)解:设半圆的半径为r米,如图,矩形的一边长为l米,根据题意,有:5r+πr+2r+2l=8,即:l=4-0.5(π+7)r又因为:l>0且r >0所以: 4-0.5(π+7)r>0则:0<r<(0<r< )变式与拓展如图,隧道横截面的下部是矩形,上部是半圆,周长为16米。
⑴求截面积S(米2)关于底部宽x(米)的函数解析式,及自变量x 的取值范围?
⑵试问:当底部宽x为几米时,隧道的截面积S最大(结果精确到0.01米)?解:∵隧道的底部宽为x,周长为16,答:当隧道的底部宽度为4.48米时,隧道的截面积最大。练一练 ( 1)已知直角三角形的两直角边的和为2。求斜
边长可能达到的最小值,以及当斜边长达到最
小值时两条直角边的长分别为多少?解:设其中一条直角边长为x,则另一条为(2-x),设斜边长为y,由勾股定理得,课堂小结本节课主要讲了将实际问题转化为数学模型.
运用二次函数求实际问题中的最大值或最小值,首先应求出函数解析式和自变量的取值范围,然后通过配方变形,或利用公式求她的最大值或最小值.值得注意的是,由此求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
同课章节目录
