二次根式的复习
图片预览

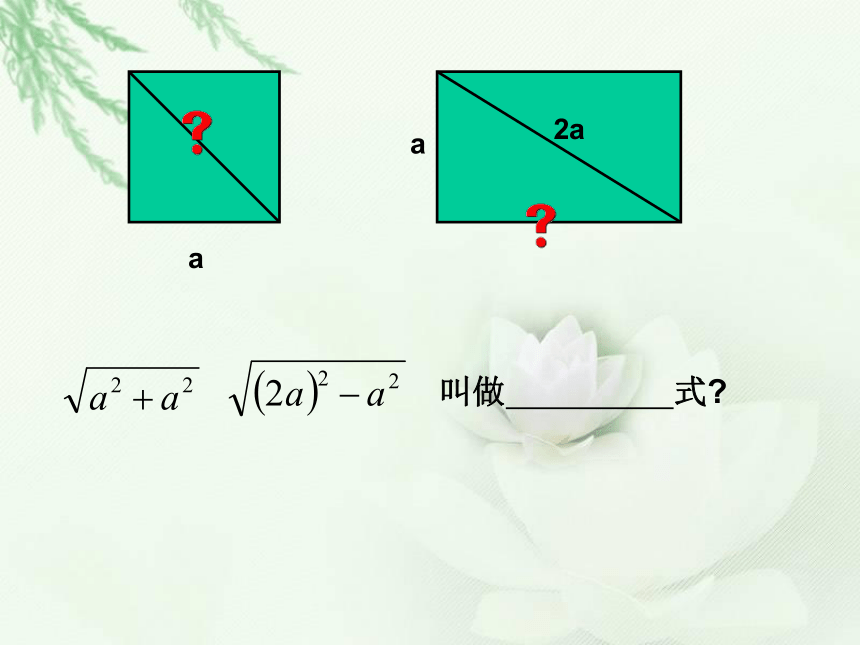







文档简介
课件22张PPT。二次根式复习a二次根式的定义:注意:被开方数大于或等于零1、二次根式的意义2. + 有意义的条件是 __ . 例2:确定二次根式中被开方数所含字母的取值范围.1.当 x__ ___时, 有意义。 3.求下列二次根式中字母的取值范围说明:二次根式被开方数不小于0,所以求二次根式中字母的取值范围常转化为不等式(组) ≤2a=3再试试你的反应2、二次根式的性质:算一算:1.将被开方数尽可能分解成几个平方数。化简二次根式的步骤:3.二次根式的运算:二次根式乘法法则二次根式除法法则二次根式的加减: 类似于合并同类项,把相同二次根式的项合并. 二次根式的混合运算: 原来学习的运算律(结合律、交换律、分配律)仍然适用,原来所学的乘法公式(如(a+b)(a-b)=a2-b2;(a±b)2=a2±2ab+b2 )仍然适用.(a≥0,b>0)怎样化去被开方数中的分母呢?(a≥0,b>0)怎样化去分母中的根号呢?注意:进行根式化简,关键是要搞清楚分式的分子和分母都乘什么,有时还要对分母进行化简。五、二次根式的混合运算例3、计算例4、计算
二次根式计算、化简的结果符合什么要求?
(1)被开方数不含分母;
分母不含根号;
根号内不含小数
(2)被开方数中不含能开得尽 方的因数或因式.最简二次根式复习回顾灵活运用1、在Rt△ABC中,∠C=90°,AB= ,AC=
求Rt△ABC的周长和面积.
A
C B应用(2)比较大小: 并说明理由.
继续拓展1.二次根式的乘除运算可以考虑先进行被开方数的约
分问题,再化简二次根式,而不一定要先将二次根式
化成最简二次根式,再约分.
2.对有关二次根式的代数式的求值问题一般应对已知
式先进行化简,代入化简后的待求式,同时还应注意
挖掘隐含条件和技巧的运用使求解更简捷.方法小结:再见
二次根式计算、化简的结果符合什么要求?
(1)被开方数不含分母;
分母不含根号;
根号内不含小数
(2)被开方数中不含能开得尽 方的因数或因式.最简二次根式复习回顾灵活运用1、在Rt△ABC中,∠C=90°,AB= ,AC=
求Rt△ABC的周长和面积.
A
C B应用(2)比较大小: 并说明理由.
继续拓展1.二次根式的乘除运算可以考虑先进行被开方数的约
分问题,再化简二次根式,而不一定要先将二次根式
化成最简二次根式,再约分.
2.对有关二次根式的代数式的求值问题一般应对已知
式先进行化简,代入化简后的待求式,同时还应注意
挖掘隐含条件和技巧的运用使求解更简捷.方法小结:再见
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
