第五章 特殊平行四边形章末复习----构造平行四边形(PPT23张)
文档属性
| 名称 | 第五章 特殊平行四边形章末复习----构造平行四边形(PPT23张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:36:34 | ||
图片预览


文档简介
(共23张PPT)
第五章 特殊平行四边形 章末复习
浙教版八年级下册
---------构造平行四边形
温故知新
1.平行四边形是中心对称图形,两条对角线的交点是它的对称中心。
O
O
构造平行四边形:
有用捕捉:对称中心:点O
有关联想:
X
“ X ”的出现
点O既是线段AC的中点,
点O又是线段BD的中点,
A'
B'
B
O
A
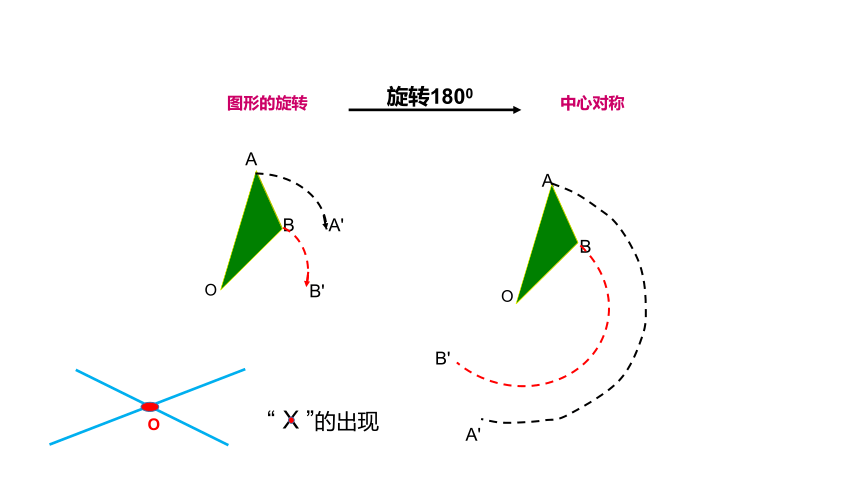
图形的旋转
中心对称
旋转1800
A'
B'
B
O
A
O
“ X ”的出现
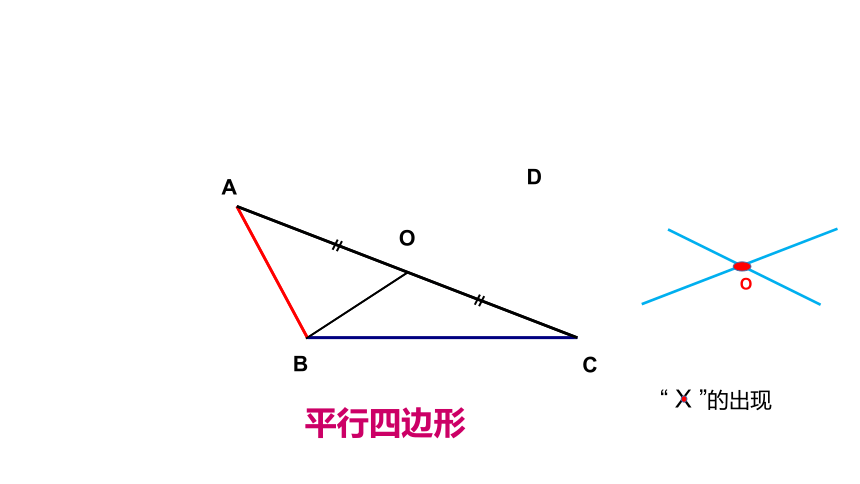
A
B
C
O
D
平行四边形
O
“ X ”的出现
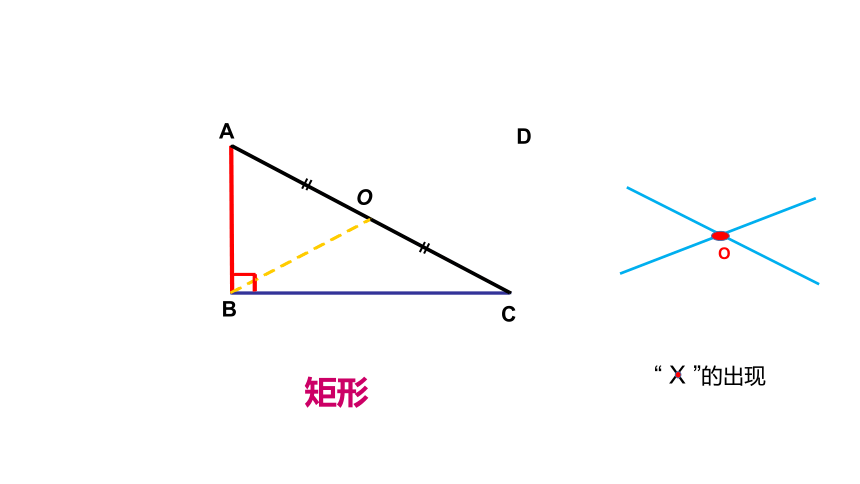
A
B
C
O
D
矩形
O
“ X ”的出现
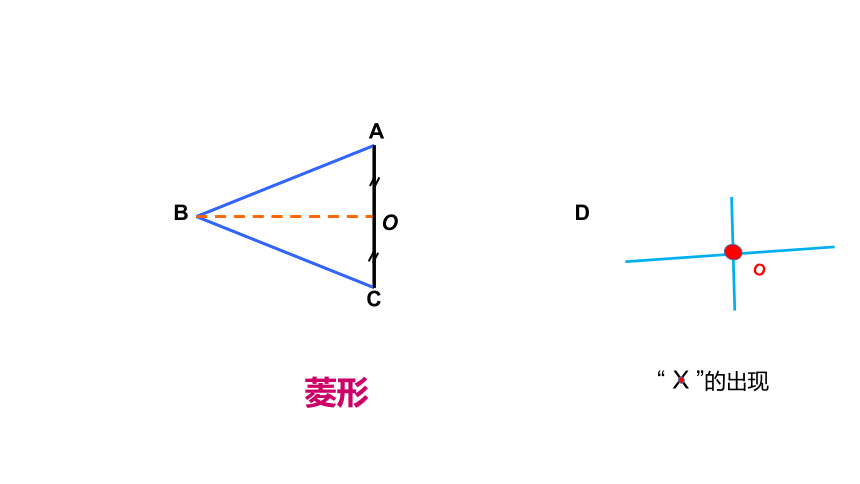
A
B
C
D
O
菱形
O
“ X ”的出现
A
B
C
O
D
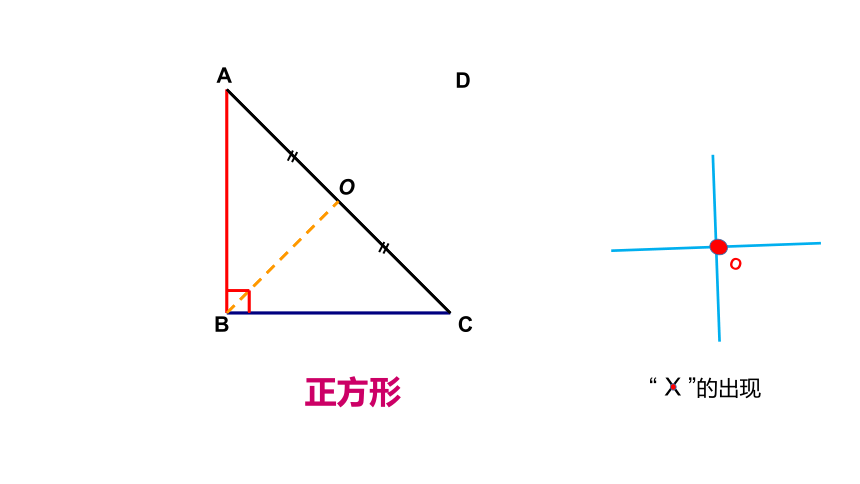
正方形
O
“ X ”的出现
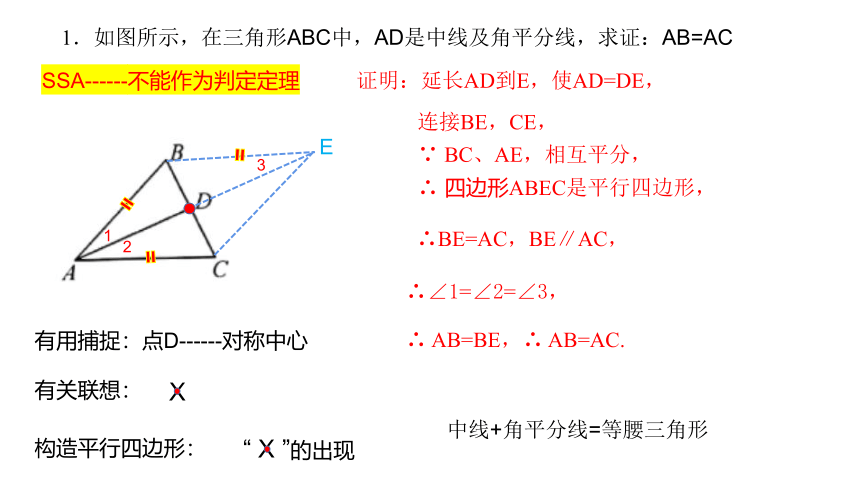
1.如图所示,在三角形ABC中,AD是中线及角平分线,求证:AB=AC
∴ AB=BE,∴ AB=AC.
E
证明:延长AD到E,使AD=DE,
连接BE,CE,
∵ BC、AE,相互平分,
∴ 四边形ABEC是平行四边形,
∴BE=AC,BE∥AC,
∴∠1=∠2=∠3,
1
2
3
有用捕捉:点D------对称中心
有关联想:
X
构造平行四边形:
“ X ”的出现
中线+角平分线=等腰三角形
SSA------不能作为判定定理
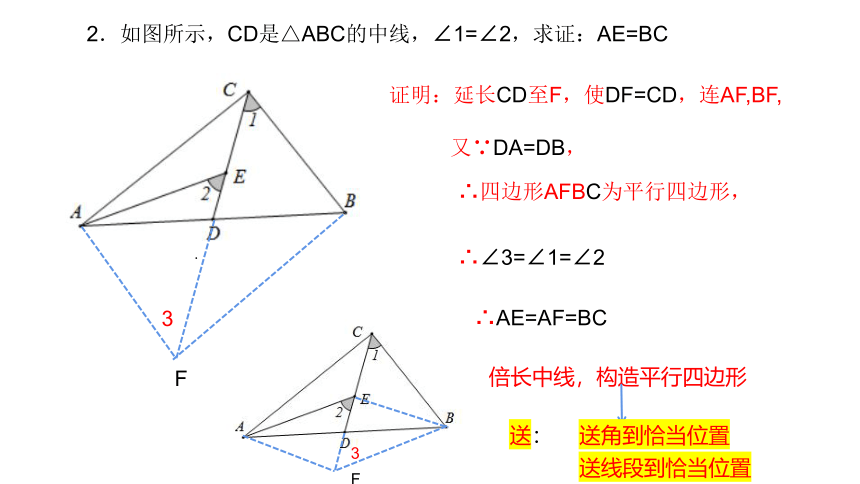
2.如图所示,CD是△ABC的中线,∠1=∠2,求证:AE=BC
.
证明:延长CD至F,使DF=CD,连AF,BF,
又∵DA=DB,
∴四边形AFBC为平行四边形,
F
∴∠3=∠1=∠2
3
F
3
倍长中线,构造平行四边形
∴AE=AF=BC
送角到恰当位置
送:
送线段到恰当位置
3.如图:直线L1,L2表示一条河的两岸,且L1∥L2,现要在这条河上建一座桥.桥建在何处,才能使从村庄A经过河到村庄B的路线最短?画出示意图,并说明理由.
解:如图,先确定AA′与河等宽,且AA′⊥河岸,连接BA′,
与河岸的交点就是点C,过点C作CD垂直河岸,交另一河岸于点D,
CD就是所求的桥的位置.
理由:由作图过程可知,四边形AA′CD为平行四边形,
AD平移至A′C即可得到线段A′B,两点之间,线段最短,
由于河宽不变,CD即为桥.
L1
L2
A
B
A′
C
D
L1
L2
结论2:两条平行线间的距离处处相等
在一条直线上任取一点作另一条平行线的垂线,
这点与垂足之间的线段长度叫做平行线间的距离
结论1:两条平行线间的距离是指夹在两条平行直线间的公垂线段的长
造桥选址---------------------
平移处理
两点间线段最短
平移处理---------------
平行四边形------------
送线段到恰当位置
A1
B1
A2
B2
A3
B3
构造
4.如图所示, ABCD中,E是BC的中点,AE=9,BD=12,AD=10.求证: AE⊥BD
F
证明:过D作DF∥AE交BC的延长线于F,
.
∵AD∥EF
∴EF=AD=10
∴四边形AEFD为平行四边形,
∴DF=AE=9
∵E是BC的中点,BE=5,BF=15
∴∠BDF=900
∵BD2+DF2=122+92=225=BF2
AE⊥BD
平移处理
构造平行四边形
送线段到恰当位置
化分散为集中
.
5.如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.证明:∠DEF=∠B
G
证明:延长EF交BC于G,
∵∠1=∠2,
∴EF∥BD,
∵∠3=∠4,
∴DE∥BC,
∴四边形DEGB是平行四边形,
∴∠DEF=∠B (平行四边形对角相等)
1
2
3
4
6.如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,求线段EG的长教育网版权所有
解:连接BD,交AC于点O,由题意知:
菱形ABCD的边长为13,
点E、F分别是边CD、BC的中点,
∴AB=BC=CD=DA=13, EFBD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵ABCD,EFBD∴DEBG,BDEG
在四边形BDEG中,∵DEBG,BDEG
∴四边形BDEG是平行四边形
∴BD=EG在△COD中,
∵OC⊥OD,CD=13,CO=12
∴OD=OB=5
∴BD=EG=10
.
.
7.如图所示,△ABC中,∠C=900,D、E分别为BC,AC上一点,BD=CE,AE=BC,求证:AD= BE
连BG,EG,
则四边形ADBG为平行四边形,
∵∠C=90°,∴∠GAE=∠C=90°,
在△AEG和△CBE中,
∴GE=BE,∠GEA=∠EBC∴∠GEB=90°.
△BEG为等腰直角三角形,
G
证明:过A作AGBD,且AG=BD,
.
平移处理---------------
构造平行四边形------------
送线段到恰当位置
AD=BG
平行四边形+K型图+等腰直角三角形
8.如图,已知AD∥BC,AB∥CD,∠B=∠BCD.
(1)求证:四边形ABCD为矩形;
(2)已知M为AD的中点,N为AB的中点,BN=2.若∠BNC=2∠DCM,求BC的长.
(1)证明:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,∠B+∠BCD=180°.
∵∠B=∠BCD,∴∠B=∠BCD=90°,
∴四边形ABCD为矩形.
(2)解:如图,延长BA,CM交于点E.
∵M为AD的中点,N为AB的中点,∴AN=BN=2,AM=MD,
∴AB=CD=4.∵AE∥DC,∴∠E=∠DCM.
在△AEM和△DCM中,AM=DM,∠AME=∠DMC,
∴△AEM≌△DCM,∴AE=CD=4.
∵∠BNC=2∠DCM=∠E+∠NCE,
∴∠NCE=∠DCM=∠E,∴CN=EN=AE+AN=4+2=6,
∴BC===4 .
.
x
2x
x
x
2
2
4
4
6
“ X ”的出现
9.如图所示是一块木板的示意图,请你用无刻度的直尺分别在三幅图中画一条直线把这块木板分成面积相等的两部分.
10.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.
M是BD的中点,求CM的长
N
“ X ”的出现------平行四边形
CM=MN=
3
3
3
4
5
11.如图,□ABCD的顶点C在等边△BEF的边BF上,点E在AB的延长线上,
G为DE的中点,连接CG.若AD=5,AB=CF=3,求CG的长
N
“ X ”的出现------平行四边形
CG=GN=
12.如图所示,△ABC中,∠ACB=900, CD⊥AB于D,AE平分∠CAB于E,交CD于F,FG∥AB交BC于G.求证:CG=BE
证明:过F作FM∥BC交AB于M,
∵FM∥BG,∴四边形为平行四边形,
M
∵∠ACD+∠BAC=90°∠B+∠BAC=90°,∴∠B=∠ACD,
∴FM=BG
∵FM∥BC
∴∠AMF=∠B
.∴
∴∠CAF=∠BAF
∵AE平分∠CAB
∴
∴CF=FM.
∴CE=CF,
∴
∴∠CEF=∠B+∠BAF=∠ACF+∠CAF=∠CFE
13. 如图①所示,在正方形ABCD和正方形CGEF中,点B,C,F在同一条直线上,M是线段AE的中点,连接DM,FM.
(1)求证:DM⊥FM,DM=FM;
(2)如图②,若将“正方形ABCD和正方形CGEF”改为“菱形
ABCD和菱形CGEF”,且∠BCD=∠G=120°,其他条件不变,则DM和FM又有怎样的位置关系和数量关系?直接写出结论.
解:(1)证明:如图,延长DM交GE于点N,连接DF,NF.
∵四边形ABCD和四边形CGEF都是正方形,∴AD∥BC,BC∥GE,
∴AD∥GE,∴∠DAM=∠NEM.∵M是AE的中点,∴AM=EM.
又∵∠AMD=∠EMN,∴△MAD≌△MEN,
∴DM=NM,AD=EN.∵AD=CD,∴CD=EN.
又∵CF=EF,∠FCD=∠FEN=90°,
∴△DCF≌△NEF,∴∠CFD=∠EFN,DF=NF.
∵DM=NM,∴FM平分∠DFN,且DM⊥FM.
∵∠EFN+∠CFN=90°,∴∠CFD+∠CFN=90°,
即∠DFN=90°.∵DM=NM,
∴FM是Rt△DFN斜边上的中线,∴DM=FM.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第五章 特殊平行四边形 章末复习
浙教版八年级下册
---------构造平行四边形
温故知新
1.平行四边形是中心对称图形,两条对角线的交点是它的对称中心。
O
O
构造平行四边形:
有用捕捉:对称中心:点O
有关联想:
X
“ X ”的出现
点O既是线段AC的中点,
点O又是线段BD的中点,
A'
B'
B
O
A
图形的旋转
中心对称
旋转1800
A'
B'
B
O
A
O
“ X ”的出现
A
B
C
O
D
平行四边形
O
“ X ”的出现
A
B
C
O
D
矩形
O
“ X ”的出现
A
B
C
D
O
菱形
O
“ X ”的出现
A
B
C
O
D
正方形
O
“ X ”的出现
1.如图所示,在三角形ABC中,AD是中线及角平分线,求证:AB=AC
∴ AB=BE,∴ AB=AC.
E
证明:延长AD到E,使AD=DE,
连接BE,CE,
∵ BC、AE,相互平分,
∴ 四边形ABEC是平行四边形,
∴BE=AC,BE∥AC,
∴∠1=∠2=∠3,
1
2
3
有用捕捉:点D------对称中心
有关联想:
X
构造平行四边形:
“ X ”的出现
中线+角平分线=等腰三角形
SSA------不能作为判定定理
2.如图所示,CD是△ABC的中线,∠1=∠2,求证:AE=BC
.
证明:延长CD至F,使DF=CD,连AF,BF,
又∵DA=DB,
∴四边形AFBC为平行四边形,
F
∴∠3=∠1=∠2
3
F
3
倍长中线,构造平行四边形
∴AE=AF=BC
送角到恰当位置
送:
送线段到恰当位置
3.如图:直线L1,L2表示一条河的两岸,且L1∥L2,现要在这条河上建一座桥.桥建在何处,才能使从村庄A经过河到村庄B的路线最短?画出示意图,并说明理由.
解:如图,先确定AA′与河等宽,且AA′⊥河岸,连接BA′,
与河岸的交点就是点C,过点C作CD垂直河岸,交另一河岸于点D,
CD就是所求的桥的位置.
理由:由作图过程可知,四边形AA′CD为平行四边形,
AD平移至A′C即可得到线段A′B,两点之间,线段最短,
由于河宽不变,CD即为桥.
L1
L2
A
B
A′
C
D
L1
L2
结论2:两条平行线间的距离处处相等
在一条直线上任取一点作另一条平行线的垂线,
这点与垂足之间的线段长度叫做平行线间的距离
结论1:两条平行线间的距离是指夹在两条平行直线间的公垂线段的长
造桥选址---------------------
平移处理
两点间线段最短
平移处理---------------
平行四边形------------
送线段到恰当位置
A1
B1
A2
B2
A3
B3
构造
4.如图所示, ABCD中,E是BC的中点,AE=9,BD=12,AD=10.求证: AE⊥BD
F
证明:过D作DF∥AE交BC的延长线于F,
.
∵AD∥EF
∴EF=AD=10
∴四边形AEFD为平行四边形,
∴DF=AE=9
∵E是BC的中点,BE=5,BF=15
∴∠BDF=900
∵BD2+DF2=122+92=225=BF2
AE⊥BD
平移处理
构造平行四边形
送线段到恰当位置
化分散为集中
.
5.如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.证明:∠DEF=∠B
G
证明:延长EF交BC于G,
∵∠1=∠2,
∴EF∥BD,
∵∠3=∠4,
∴DE∥BC,
∴四边形DEGB是平行四边形,
∴∠DEF=∠B (平行四边形对角相等)
1
2
3
4
6.如图,菱形ABCD的边长为13,对角线AC=24,点E、F分别是边CD、BC的中点,连接EF并延长与AB的延长线相交于点G,求线段EG的长教育网版权所有
解:连接BD,交AC于点O,由题意知:
菱形ABCD的边长为13,
点E、F分别是边CD、BC的中点,
∴AB=BC=CD=DA=13, EFBD,
∵AC、BD是菱形的对角线,AC=24,
∴AC⊥BD,AO=CO=12,OB=OD,
又∵ABCD,EFBD∴DEBG,BDEG
在四边形BDEG中,∵DEBG,BDEG
∴四边形BDEG是平行四边形
∴BD=EG在△COD中,
∵OC⊥OD,CD=13,CO=12
∴OD=OB=5
∴BD=EG=10
.
.
7.如图所示,△ABC中,∠C=900,D、E分别为BC,AC上一点,BD=CE,AE=BC,求证:AD= BE
连BG,EG,
则四边形ADBG为平行四边形,
∵∠C=90°,∴∠GAE=∠C=90°,
在△AEG和△CBE中,
∴GE=BE,∠GEA=∠EBC∴∠GEB=90°.
△BEG为等腰直角三角形,
G
证明:过A作AGBD,且AG=BD,
.
平移处理---------------
构造平行四边形------------
送线段到恰当位置
AD=BG
平行四边形+K型图+等腰直角三角形
8.如图,已知AD∥BC,AB∥CD,∠B=∠BCD.
(1)求证:四边形ABCD为矩形;
(2)已知M为AD的中点,N为AB的中点,BN=2.若∠BNC=2∠DCM,求BC的长.
(1)证明:∵AD∥BC,AB∥CD,
∴四边形ABCD是平行四边形,∠B+∠BCD=180°.
∵∠B=∠BCD,∴∠B=∠BCD=90°,
∴四边形ABCD为矩形.
(2)解:如图,延长BA,CM交于点E.
∵M为AD的中点,N为AB的中点,∴AN=BN=2,AM=MD,
∴AB=CD=4.∵AE∥DC,∴∠E=∠DCM.
在△AEM和△DCM中,AM=DM,∠AME=∠DMC,
∴△AEM≌△DCM,∴AE=CD=4.
∵∠BNC=2∠DCM=∠E+∠NCE,
∴∠NCE=∠DCM=∠E,∴CN=EN=AE+AN=4+2=6,
∴BC===4 .
.
x
2x
x
x
2
2
4
4
6
“ X ”的出现
9.如图所示是一块木板的示意图,请你用无刻度的直尺分别在三幅图中画一条直线把这块木板分成面积相等的两部分.
10.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.
M是BD的中点,求CM的长
N
“ X ”的出现------平行四边形
CM=MN=
3
3
3
4
5
11.如图,□ABCD的顶点C在等边△BEF的边BF上,点E在AB的延长线上,
G为DE的中点,连接CG.若AD=5,AB=CF=3,求CG的长
N
“ X ”的出现------平行四边形
CG=GN=
12.如图所示,△ABC中,∠ACB=900, CD⊥AB于D,AE平分∠CAB于E,交CD于F,FG∥AB交BC于G.求证:CG=BE
证明:过F作FM∥BC交AB于M,
∵FM∥BG,∴四边形为平行四边形,
M
∵∠ACD+∠BAC=90°∠B+∠BAC=90°,∴∠B=∠ACD,
∴FM=BG
∵FM∥BC
∴∠AMF=∠B
.∴
∴∠CAF=∠BAF
∵AE平分∠CAB
∴
∴CF=FM.
∴CE=CF,
∴
∴∠CEF=∠B+∠BAF=∠ACF+∠CAF=∠CFE
13. 如图①所示,在正方形ABCD和正方形CGEF中,点B,C,F在同一条直线上,M是线段AE的中点,连接DM,FM.
(1)求证:DM⊥FM,DM=FM;
(2)如图②,若将“正方形ABCD和正方形CGEF”改为“菱形
ABCD和菱形CGEF”,且∠BCD=∠G=120°,其他条件不变,则DM和FM又有怎样的位置关系和数量关系?直接写出结论.
解:(1)证明:如图,延长DM交GE于点N,连接DF,NF.
∵四边形ABCD和四边形CGEF都是正方形,∴AD∥BC,BC∥GE,
∴AD∥GE,∴∠DAM=∠NEM.∵M是AE的中点,∴AM=EM.
又∵∠AMD=∠EMN,∴△MAD≌△MEN,
∴DM=NM,AD=EN.∵AD=CD,∴CD=EN.
又∵CF=EF,∠FCD=∠FEN=90°,
∴△DCF≌△NEF,∴∠CFD=∠EFN,DF=NF.
∵DM=NM,∴FM平分∠DFN,且DM⊥FM.
∵∠EFN+∠CFN=90°,∴∠CFD+∠CFN=90°,
即∠DFN=90°.∵DM=NM,
∴FM是Rt△DFN斜边上的中线,∴DM=FM.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
