浙教版九年级上册第3章 圆的基本性质 课件(共44张PPT)
文档属性
| 名称 | 浙教版九年级上册第3章 圆的基本性质 课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 548.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 07:29:36 | ||
图片预览







文档简介
(共44张PPT)
数学解题与变式教学
一、关于解题的认识
掌握数学就意味着善于解题。
------数学家波利亚
学生通过做数学题学会分析问题、转化问题、解决问题,以后他们可以运用在解数学题的过程中获得的经验去解决各种现实问题,而解题所形成的理念、习惯、程序将伴随孩子一生.
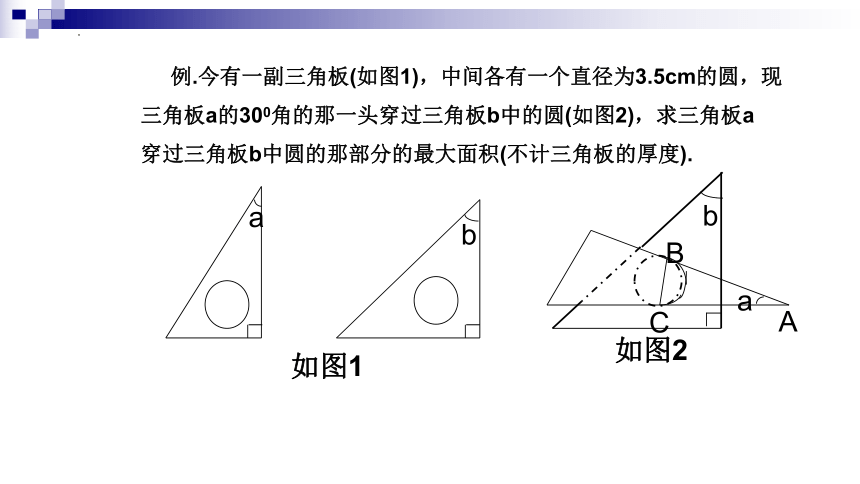
例.今有一副三角板(如图1),中间各有一个直径为3.5cm的圆,现
三角板a的300角的那一头穿过三角板b中的圆(如图2),求三角板a
穿过三角板b中圆的那部分的最大面积(不计三角板的厚度).
b
a
B
C
A
如图2
a
b
如图1
A
图3
a
C
B
b
a
B
C
A
如图2
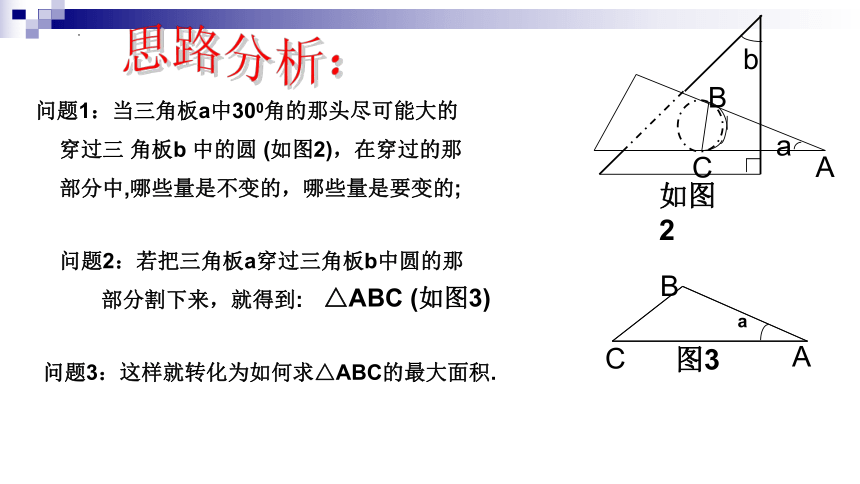
问题1:当三角板a中300角的那头尽可能大的
穿过三 角板b 中的圆 (如图2),在穿过的那
部分中,哪些量是不变的,哪些量是要变的;
问题2:若把三角板a穿过三角板b中圆的那
部分割下来,就得到:
问题3:这样就转化为如何求△ABC的最大面积.
△ABC (如图3)
思路分析:
A
知识点探究1:
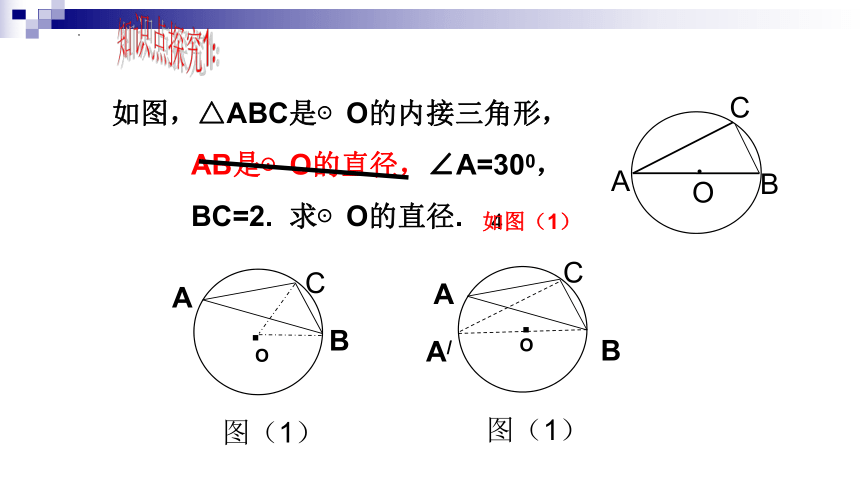
如图,△ABC是⊙O的内接三角形,
AB是⊙O的直径,∠A=300,
BC=2. 求⊙O的直径.
4
如图(1)
·
B
C
O
·
O
A
B
C
图(1)
C
·
O
A
B
A/
图(1)
变式二:△ABC中,满足∠A=300, BC=2.
·
0
A
B
C
A/
问题1: 满足条件的△ABC我们能画出几个?
AB的最大值为4.
问题2:在运动过程中线段AB有最大值吗 ?
有规律吗?
问题3:在运动过程中, △ABC有最大面积吗?
只要BC边上的高最大,即A到BC边的距离最大.
此时点A运动到BC的垂直平分线上时,
即BC边上的高最大如图(2).
·
0
B
C
A/
A
OC=BC=2,OD=
∴ △ABC的最大面积
=
分析如图(2):
图2
有
连OB、OC
D
3、优化学生思维素质
2、掌握贯通数学思想
1、培养学习兴趣,提高教学效益
二、关于变式的认识
1、培养学习兴趣,提高教学效益
通过变式教学,有效地帮助学生理解学习对象的本质属性以及建立学习对象与已有知识的内在合理联系。锻炼学生的逻辑思维,提高课堂教学的有效性,也就是提高学生自我学习、自我发现、自我反思、自我发展、自我完善的能力,从而全面减轻学生过重的课业负担,真正达到“轻负高质”。
例1. 求证:顺次连结平行四边形各边中点所得的四边形是平行四边形。
变式1、求证:顺次连结矩形各边中点所得的四边形是菱形。
变式2、求证:顺次连结菱形各边中点所得的四边形是矩形。
变式3、求证:顺次连结正方形各边中点所得的四边形是正方形。
变式5、顺次连结什么四边形中点得到矩形。
变式6、顺次连结什么四边形中点得到菱形等。
变式4、顺次连结什么四边形中点得到平行四边形。
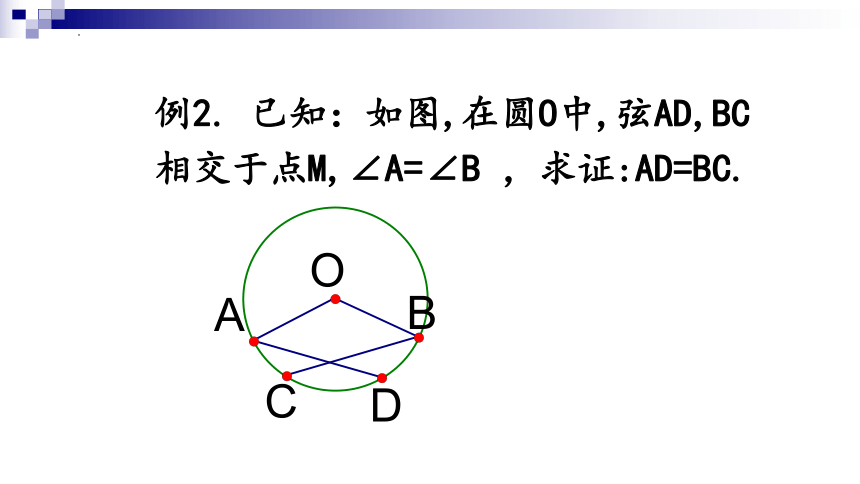
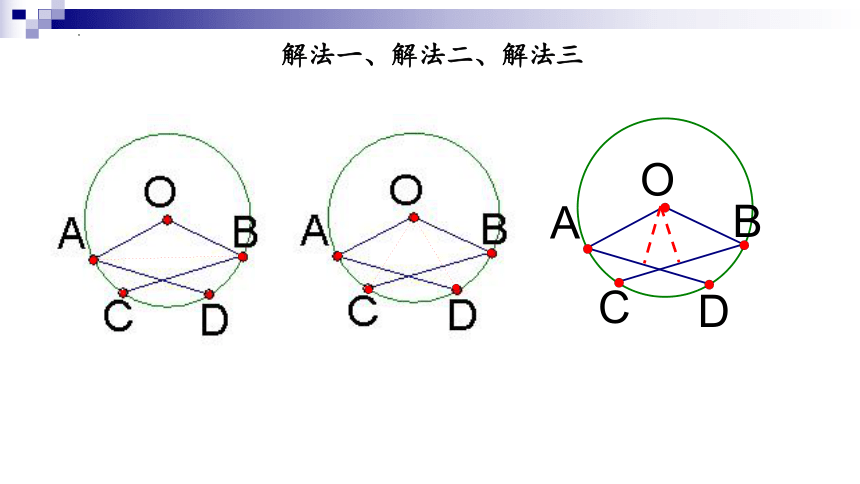
例2. 已知:如图,在圆O中,弦AD,BC
相交于点M,∠A=∠B ,求证:AD=BC.
解法一、解法二、解法三
解法四、解法五、解法六
例3 如图,矩形ABCD中,AB=4,BC=6。
(1)在图1中,E、F、G、H分别是AD、AB、BC、CD的中点,求菱形EFGH的面积;
(图1)
(2)在图2中,若E,F在AD,BC上,且BEDF是菱形,求这个菱形的面积。
(图2)
变式:
(1)在图2中画出一个比(1)中的菱形面积更大的菱形,并计算所画菱形的面积。
(2)在图3中画出一个比(2)中的菱形面积更大的菱形,并计算所画菱形的面积。
(图2)
(图3)
2、掌握贯通数学思想
二、关于变式的认识
通过变式教学,解决如何优化学生思维素质的问题,以及如何使学生贯通数学思想的问题。
例4.已知点P(a-2,a2-4)在x轴负半轴上,求点P坐标
变式1已知P(a-2,a2-4)在二、四象限的角平分线上,求点P坐标
变式2若点P(a-2,a2-4)在直线y=2x+3上,求点P的坐标.
变式3已知点A(-3,m)、B(n,4),若AB∥x轴,求m的值并确定n的范围.
例5.如图,在直角梯形ABCD中,
∠A=∠B=90°,E在AB上,
DE⊥EC,AD+DE=AB=8,
那么△BCE的周长等于 ▲
_
C
_
E
_
B
_
A
_
D
如图,在直角梯形ABCD中,
∠A=∠B=90°,E在AB上,
DE⊥EC,AD+DE=AB=8,
那么△BCE的周长等于 ▲
解:设 则
在Rt△ADE中 , 即
_
C
_
E
_
B
_
A
_
D
E
B
A
C
D
变式:
如图,在四边形ABCD中,
E是BC上的一点,
∠AED=∠B=∠C=60°
AB+AE=BC=8,BE=2,
则△CDE的周长为 。
例6. 如图,∠C=90°,∠A=30°,D在AC上,∠BDC=45°,一个常见的图形中有一个很容易被忽视的结论:
AB= BD
变式:如图AB是⊙O的直径,C在圆上,∠BAC=30°,D在AC上,CD=CB,E在弧AC上,∠EAB=45°。
求证:AD=ED.
例7.如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。
变式题1:如图,已知AD、BE分别是△ABC的BC、AC边上的高,F是DE的中点,G是AB的中点,则FG⊥DE,请说明理由。
变式题2:如图,四边形ABCD中,∠DAB=∠DCB=90°,点M,N分别是BD、AC的中点,MN、AC的位置关系如何?
A
B
C
D
M
N
变式题3:如图,线段AC与BD交于点O,连结BC,已知BO=BA,CO=CD,E,F,GF分别为OD,OA,BC的中点。
求证:FG=EG
C
A
B
D
E
O
G
F
3、优化学生思维素质
二、关于变式的认识
通过变式教学,教学通过对数学问题多角度、多方位、多层次的讨论和思考,帮助学生打通关节,建构有价值的变式探索研究,展示数学知识发生、发展和应用的过程,有意识、有目的地引导学生从“变”的现象中发现“不变”的本质,从“不变”的本质中探究“变”的规律,使所有知识点融会贯通,使思维在所学知识中游刃有余、顺畅飞翔。
问题一:要在河边修建一个水泵站,分别向两侧的村庄A,B
送水,问水泵站应修建在河边的什么地方,可使所用的水管
最短?
请你来设计方案,怎样设计才能使所用的水管最短?
画一画
问题二:要在河边修建一个水泵站,分别向同侧的村庄A,B
送水,问水泵站应修建在河边的什么地方,可使所用的水管
最短?
例10:在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,则BP+PE最小值_____
解:B的对称点为C,连接CP只要C,P,E三点共线即可
D
变外形
变式1:在等边三角形ABC中,AB=2,点E是AB的中点,在BC上找一点P,使AP+PE最小,则最小值是_______
解:作E的对称点E',连接PE',延长E'E,作AF⊥E'F
∵AP+PE=AP+PE’
∴A,P,E'三点共线时最小
方法二:
解:作A的对称点A',连接A’E,A’B
∵AP+PE=A’P+PE
∴A’,P,E三点共线时最小
变式2:设正三角形ABC的边长为2,E为AB上
的中点,P为BC边上的任意一点,PA+PE的
最大值和最小值分别记为s和t 。
求s2-t2=__。(2005.全国初中数学竞赛题)
解:由上题可知最小值为
当P运动到于C重合时最大,
最大值为
变式3:如图,在正方形ABCD中,E在BC上,BE=2,
CE=1,P在BD上,则PE和PC的长度之和最小可达到____。
解:由正方形的对称性质,可知点E关
于BD的对称点E'在AB上,连CE'交BD
于P,则PE+PC最小
此时PE'=BE=2
PE'=PE,PE+PC=PE'+PC=CE‘
E
A
B
C
D
P
E’
变式4:如图,已知⊙O的半径为r,C、D是直径AB同侧圆
周上的两点,AC的度数为96°,BD的度数为36°,动点P在
AB上,则CP+PD的最小值为____。
解:如图,设D'是D关于直径AB的对
称点,连CD‘交AB于P
则P点使CP+PD最小。
∵AC=96°,BD=36°,
∴CD=180°-96°-36°=48°
∴CD‘=48°+36°×2=120°,
∴∠COD'=120°。
从而易求CP+PD=CD'=
D'
变式5:如图,平面直角坐标系中,分别以点A(2,3),点B(3,4)为圆心,1,3为半径作圆A,圆B,M,N分别是圆A,圆B上动点,P为X轴上的动点,则PM+PN的最小值
解析:作圆A关于X轴的对称圆A’,连接BA’分别交圆A’和圆B于M,N,交X轴于P,此时PM+PN最小
A’B=
即PA+PB的最小值为
变式6:如图,在第一象限上有两点A(2,3),B(4,5)请在x轴上找点P,则AP+BP最小值是_____
解:作点A关于直线l的对称点A',连结
A'B交直线l于点p,两线段的和
AP+BP=A'P+BP
=A'B=
变式7:求代数式
的最小值。
41
8
13
4
2
2
+
-
+
+
-
x
x
x
x
解答要点:如图,参考上题可知
=
=
变式8:求代数式
的最大值。
解:连接BA
并延长交x轴于点C
AB即为差的最大值
变式9:如图,在第一象限上有两点A(2,3),B(4,-5)请在x轴找一点P,则 最大值是_____
解:作B的对称点B’,连接B’A
并延长交x轴于P
AB’为 的最大值
变式10:如图,在第一象限上有两点A(2,3),B(4,-5)请在x轴找一点P,则 最小值时,P的坐标______
解:连接AB,作AB的中垂线
交X轴于点P
∴P(7,0)
(7,0)
方法一:
设P(x,0)
∵AP=BP
∴AP2=BP2
∴(x-2)2+9=(x-4)2+25
∴x=7
变式11:如图,在第一象限上有两点A(2,3),B(4,-5)请在x轴找一点P,则 最小值时,P的坐标______
解:连接AB,作AB的中垂线,交X轴于点P
∵LAB:y=-4x+11
∴P(7,0)
(7,0)
∴直线AB的中垂线的解析式:
方法二:
三、关于反思的认识
数学素质教育的核心是培养学生解决问题的能力,而解决问题是数学核心的思维活动,教师教学后的反思,在于不断总结、积累教育教学经验,构建高效课堂。学生在变式教学活动中,通过问题的解决和反思,能不断丰富解决问题的方法和策略,从而提高解题的效率,促进数学素质的提升。
思维品质
灵活性
深刻性
独创性
批判性
敏捷性
系统性
谢谢
大家
数学解题与变式教学
一、关于解题的认识
掌握数学就意味着善于解题。
------数学家波利亚
学生通过做数学题学会分析问题、转化问题、解决问题,以后他们可以运用在解数学题的过程中获得的经验去解决各种现实问题,而解题所形成的理念、习惯、程序将伴随孩子一生.
例.今有一副三角板(如图1),中间各有一个直径为3.5cm的圆,现
三角板a的300角的那一头穿过三角板b中的圆(如图2),求三角板a
穿过三角板b中圆的那部分的最大面积(不计三角板的厚度).
b
a
B
C
A
如图2
a
b
如图1
A
图3
a
C
B
b
a
B
C
A
如图2
问题1:当三角板a中300角的那头尽可能大的
穿过三 角板b 中的圆 (如图2),在穿过的那
部分中,哪些量是不变的,哪些量是要变的;
问题2:若把三角板a穿过三角板b中圆的那
部分割下来,就得到:
问题3:这样就转化为如何求△ABC的最大面积.
△ABC (如图3)
思路分析:
A
知识点探究1:
如图,△ABC是⊙O的内接三角形,
AB是⊙O的直径,∠A=300,
BC=2. 求⊙O的直径.
4
如图(1)
·
B
C
O
·
O
A
B
C
图(1)
C
·
O
A
B
A/
图(1)
变式二:△ABC中,满足∠A=300, BC=2.
·
0
A
B
C
A/
问题1: 满足条件的△ABC我们能画出几个?
AB的最大值为4.
问题2:在运动过程中线段AB有最大值吗 ?
有规律吗?
问题3:在运动过程中, △ABC有最大面积吗?
只要BC边上的高最大,即A到BC边的距离最大.
此时点A运动到BC的垂直平分线上时,
即BC边上的高最大如图(2).
·
0
B
C
A/
A
OC=BC=2,OD=
∴ △ABC的最大面积
=
分析如图(2):
图2
有
连OB、OC
D
3、优化学生思维素质
2、掌握贯通数学思想
1、培养学习兴趣,提高教学效益
二、关于变式的认识
1、培养学习兴趣,提高教学效益
通过变式教学,有效地帮助学生理解学习对象的本质属性以及建立学习对象与已有知识的内在合理联系。锻炼学生的逻辑思维,提高课堂教学的有效性,也就是提高学生自我学习、自我发现、自我反思、自我发展、自我完善的能力,从而全面减轻学生过重的课业负担,真正达到“轻负高质”。
例1. 求证:顺次连结平行四边形各边中点所得的四边形是平行四边形。
变式1、求证:顺次连结矩形各边中点所得的四边形是菱形。
变式2、求证:顺次连结菱形各边中点所得的四边形是矩形。
变式3、求证:顺次连结正方形各边中点所得的四边形是正方形。
变式5、顺次连结什么四边形中点得到矩形。
变式6、顺次连结什么四边形中点得到菱形等。
变式4、顺次连结什么四边形中点得到平行四边形。
例2. 已知:如图,在圆O中,弦AD,BC
相交于点M,∠A=∠B ,求证:AD=BC.
解法一、解法二、解法三
解法四、解法五、解法六
例3 如图,矩形ABCD中,AB=4,BC=6。
(1)在图1中,E、F、G、H分别是AD、AB、BC、CD的中点,求菱形EFGH的面积;
(图1)
(2)在图2中,若E,F在AD,BC上,且BEDF是菱形,求这个菱形的面积。
(图2)
变式:
(1)在图2中画出一个比(1)中的菱形面积更大的菱形,并计算所画菱形的面积。
(2)在图3中画出一个比(2)中的菱形面积更大的菱形,并计算所画菱形的面积。
(图2)
(图3)
2、掌握贯通数学思想
二、关于变式的认识
通过变式教学,解决如何优化学生思维素质的问题,以及如何使学生贯通数学思想的问题。
例4.已知点P(a-2,a2-4)在x轴负半轴上,求点P坐标
变式1已知P(a-2,a2-4)在二、四象限的角平分线上,求点P坐标
变式2若点P(a-2,a2-4)在直线y=2x+3上,求点P的坐标.
变式3已知点A(-3,m)、B(n,4),若AB∥x轴,求m的值并确定n的范围.
例5.如图,在直角梯形ABCD中,
∠A=∠B=90°,E在AB上,
DE⊥EC,AD+DE=AB=8,
那么△BCE的周长等于 ▲
_
C
_
E
_
B
_
A
_
D
如图,在直角梯形ABCD中,
∠A=∠B=90°,E在AB上,
DE⊥EC,AD+DE=AB=8,
那么△BCE的周长等于 ▲
解:设 则
在Rt△ADE中 , 即
_
C
_
E
_
B
_
A
_
D
E
B
A
C
D
变式:
如图,在四边形ABCD中,
E是BC上的一点,
∠AED=∠B=∠C=60°
AB+AE=BC=8,BE=2,
则△CDE的周长为 。
例6. 如图,∠C=90°,∠A=30°,D在AC上,∠BDC=45°,一个常见的图形中有一个很容易被忽视的结论:
AB= BD
变式:如图AB是⊙O的直径,C在圆上,∠BAC=30°,D在AC上,CD=CB,E在弧AC上,∠EAB=45°。
求证:AD=ED.
例7.如图,已知AD⊥BD,AC⊥BC,E为AB的中点,试判断DE与CE是否相等,并说明理由。
变式题1:如图,已知AD、BE分别是△ABC的BC、AC边上的高,F是DE的中点,G是AB的中点,则FG⊥DE,请说明理由。
变式题2:如图,四边形ABCD中,∠DAB=∠DCB=90°,点M,N分别是BD、AC的中点,MN、AC的位置关系如何?
A
B
C
D
M
N
变式题3:如图,线段AC与BD交于点O,连结BC,已知BO=BA,CO=CD,E,F,GF分别为OD,OA,BC的中点。
求证:FG=EG
C
A
B
D
E
O
G
F
3、优化学生思维素质
二、关于变式的认识
通过变式教学,教学通过对数学问题多角度、多方位、多层次的讨论和思考,帮助学生打通关节,建构有价值的变式探索研究,展示数学知识发生、发展和应用的过程,有意识、有目的地引导学生从“变”的现象中发现“不变”的本质,从“不变”的本质中探究“变”的规律,使所有知识点融会贯通,使思维在所学知识中游刃有余、顺畅飞翔。
问题一:要在河边修建一个水泵站,分别向两侧的村庄A,B
送水,问水泵站应修建在河边的什么地方,可使所用的水管
最短?
请你来设计方案,怎样设计才能使所用的水管最短?
画一画
问题二:要在河边修建一个水泵站,分别向同侧的村庄A,B
送水,问水泵站应修建在河边的什么地方,可使所用的水管
最短?
例10:在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,则BP+PE最小值_____
解:B的对称点为C,连接CP只要C,P,E三点共线即可
D
变外形
变式1:在等边三角形ABC中,AB=2,点E是AB的中点,在BC上找一点P,使AP+PE最小,则最小值是_______
解:作E的对称点E',连接PE',延长E'E,作AF⊥E'F
∵AP+PE=AP+PE’
∴A,P,E'三点共线时最小
方法二:
解:作A的对称点A',连接A’E,A’B
∵AP+PE=A’P+PE
∴A’,P,E三点共线时最小
变式2:设正三角形ABC的边长为2,E为AB上
的中点,P为BC边上的任意一点,PA+PE的
最大值和最小值分别记为s和t 。
求s2-t2=__。(2005.全国初中数学竞赛题)
解:由上题可知最小值为
当P运动到于C重合时最大,
最大值为
变式3:如图,在正方形ABCD中,E在BC上,BE=2,
CE=1,P在BD上,则PE和PC的长度之和最小可达到____。
解:由正方形的对称性质,可知点E关
于BD的对称点E'在AB上,连CE'交BD
于P,则PE+PC最小
此时PE'=BE=2
PE'=PE,PE+PC=PE'+PC=CE‘
E
A
B
C
D
P
E’
变式4:如图,已知⊙O的半径为r,C、D是直径AB同侧圆
周上的两点,AC的度数为96°,BD的度数为36°,动点P在
AB上,则CP+PD的最小值为____。
解:如图,设D'是D关于直径AB的对
称点,连CD‘交AB于P
则P点使CP+PD最小。
∵AC=96°,BD=36°,
∴CD=180°-96°-36°=48°
∴CD‘=48°+36°×2=120°,
∴∠COD'=120°。
从而易求CP+PD=CD'=
D'
变式5:如图,平面直角坐标系中,分别以点A(2,3),点B(3,4)为圆心,1,3为半径作圆A,圆B,M,N分别是圆A,圆B上动点,P为X轴上的动点,则PM+PN的最小值
解析:作圆A关于X轴的对称圆A’,连接BA’分别交圆A’和圆B于M,N,交X轴于P,此时PM+PN最小
A’B=
即PA+PB的最小值为
变式6:如图,在第一象限上有两点A(2,3),B(4,5)请在x轴上找点P,则AP+BP最小值是_____
解:作点A关于直线l的对称点A',连结
A'B交直线l于点p,两线段的和
AP+BP=A'P+BP
=A'B=
变式7:求代数式
的最小值。
41
8
13
4
2
2
+
-
+
+
-
x
x
x
x
解答要点:如图,参考上题可知
=
=
变式8:求代数式
的最大值。
解:连接BA
并延长交x轴于点C
AB即为差的最大值
变式9:如图,在第一象限上有两点A(2,3),B(4,-5)请在x轴找一点P,则 最大值是_____
解:作B的对称点B’,连接B’A
并延长交x轴于P
AB’为 的最大值
变式10:如图,在第一象限上有两点A(2,3),B(4,-5)请在x轴找一点P,则 最小值时,P的坐标______
解:连接AB,作AB的中垂线
交X轴于点P
∴P(7,0)
(7,0)
方法一:
设P(x,0)
∵AP=BP
∴AP2=BP2
∴(x-2)2+9=(x-4)2+25
∴x=7
变式11:如图,在第一象限上有两点A(2,3),B(4,-5)请在x轴找一点P,则 最小值时,P的坐标______
解:连接AB,作AB的中垂线,交X轴于点P
∵LAB:y=-4x+11
∴P(7,0)
(7,0)
∴直线AB的中垂线的解析式:
方法二:
三、关于反思的认识
数学素质教育的核心是培养学生解决问题的能力,而解决问题是数学核心的思维活动,教师教学后的反思,在于不断总结、积累教育教学经验,构建高效课堂。学生在变式教学活动中,通过问题的解决和反思,能不断丰富解决问题的方法和策略,从而提高解题的效率,促进数学素质的提升。
思维品质
灵活性
深刻性
独创性
批判性
敏捷性
系统性
谢谢
大家
同课章节目录
