浙教数学九年级上第三章 圆的基本性质 综合素质评价(含答案)
文档属性
| 名称 | 浙教数学九年级上第三章 圆的基本性质 综合素质评价(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 700.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-21 09:03:23 | ||
图片预览




文档简介
九上·第3章 圆的基本性质 综合素质评价
一、选择题(每题3分,共30分)
1.已知⊙O的半径为5 cm,点A是线段OP的中点,当OP=8 cm时,点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O上
C.点A在⊙O内 D.不能确定
2.[2023·宁波余姚市期中]下列事件中,属于必然事件的是( )
A. 三个点确定一个圆
B.每条边都相等的多边形是正多边形
C.平分弦的直径垂直于弦
D.直径所对的圆周角是直角
3.[2023·杭州临平区期中]如图,在同一平面内,将边长相等的正六边形、正方形的一边重合,则∠1的度数为( )
A.18° B.25° C.30° D.45°
4.如图,在4×4的正方形网格中,每个小正方形的边长均为1,若将△ABC绕点A逆时针旋转得到△AB′C′,则的长为( )
A.π B. C.7π D.6π
5.如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是( )
A.4 B.6 C.8 D.10
6.[2023·温州瑞安市期中]如图,四边形ABCD内接于⊙O,点E为上一点,连结BE,DE.若∠A+∠ABC+∠ADC=240°,则∠E=( )
A.55° B.60° C.65° D.70°
7.如图,将菱形ABCD绕点A逆时针旋转α得到菱形AB′C′D′,∠B=β.若AC平分∠B′AC′,则α与β满足的数量关系是( )
A.α=2β B.2α=3β C.4α+β=180° D.3α+2β=180°
8.如图,AB是⊙O的直径,点C,D在⊙O上,且OD经过AC的中点E,连结DC并延长,与AB的延长线相交于点P,若∠CAB=16°,则∠BPC的度数为( )
A.16° B.21° C.32° D.37°
9.如图,⊙O过点B,C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.2 B. C.4 D.3
10.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为劣弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A. B.1 C.2 D.2
二、填空题(每题4分,共24分)
11.[2023·宁波余姚市月考]直角三角形的两边长分别为5和12,则此三角形的外接圆的半径是________.
12.如图,在矩形ABCD中,AB=1,AD=2,将AD绕点A顺时针旋转,点D落在BC上的点D′处,则∠DAD′=________°.
13.如图,A,B,C为⊙O上的点,若∠ACB=20°,则∠BAO的度数为________°.
14.如图,在5×3的网格图中,每个小正方形的边长均为1,设经过格点A,C,B的圆弧与BD交于点E,则阴影部分的面积为__________.(结果保留π)
15.如图,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连结AE.若∠BCD=2∠BAD,则∠DAE的度数是________.
16.[2023·温州龙港市期中]如图,半圆O的直径为AB,AB=2,点C是半圆O上的任意一点,点F是的中点,连结BF交AC于点E,AD平分∠CAB交BF于点D,则∠ADB=________°;当DB=DF时,BC的长为________.
三、解答题(17~19题每题6分,20,21题每题8分,22,23题每题10分,24题12分,共66分)
17.[2023·台州期中]如图,在⊙O中,∠ABD=∠CDB,求证:CD=AB.
18.如图,在⊙O中,已知AB=AC,∠APC=60°.
(1)求证:△ABC是等边三角形.
(2)求∠APB的度数.
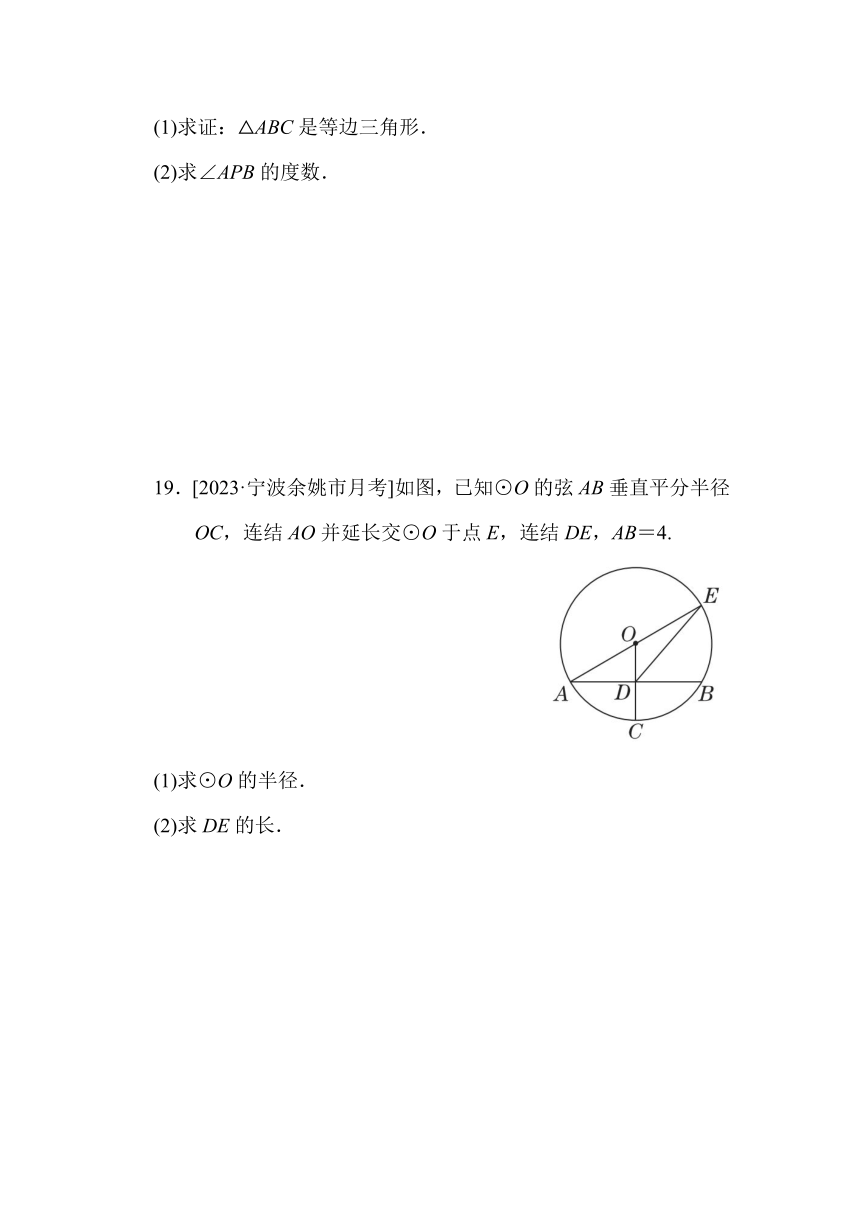
19.[2023·宁波余姚市月考]如图,已知⊙O的弦AB垂直平分半径OC,连结AO并延长交⊙O于点E,连结DE,AB=4.
(1)求⊙O的半径.
(2)求DE的长.
20.如图,已知AB是⊙O的直径,弦AC与半径OD平行.
(1)求证:点D是的中点.
(2)若AC=OD=6,求阴影部分的面积.
21.如图,在⊙O中,==,OC与AD相交于点E,连结BE,BC,CD.求证:
(1)AD∥BC.
(2)四边形BCDE为菱形.
22.如图,已知在△ABC中,AB=AC,∠BAC=120°,在BC边上取一点O,以点O为圆心、OB为半径作圆,且⊙O过点A.
(1)若⊙O的半径为5,求线段OC的长.
(2)过点A作AD∥BC交⊙O于点D,连结BD,求的值.
23.如图是一拱形桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.
(1)求桥拱所在圆的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
24.【问题提出】
如图①,AB,AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,求证:CD=AB+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
证明:如图②,延长CA至点E,使AE=AB,连结MA,MB,MC,ME,BC.
∵M是的中点,∴=,
∴∠MCB=∠MBC,MB=MC.(请你在下面的空白处补全小敏的证明过程)
【推广运用】
如图③,等边三角形ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是________.
【拓展研究】
如图④,若将【问题提出】中的“M是的中点”改成“M是的中点”,其余条件不变,“CD=AB+AD”这一结论还成立吗?若成立,请说明理由;若不成立,请写出CD,AB,AD三者之间的数量关系,并说明理由.
INCLUDEPICTURE "../../七八九/4章上.EPS" \* MERGEFORMAT INCLUDEPICTURE "../4章上.EPS" \* MERGEFORMAT \d 答案
一、1.C 2.C 3.A
4.C 【点拨】连结OA,
∵半径OC⊥AB,
∴2AE=AB.
∵OC=5,CE=2,∴OE=3.
在Rt△AOE中,OA=5,
∴AE==4,
∴AB=2AE=8.
5.D 6.B
7.C 【点拨】∵AC平分∠B′AC′,
∴∠B′AC=∠C′AC.
又∵∠BAC=∠DAC,
∴∠BAB′=∠DAC′.
由旋转的性质,得∠BAB′=∠C′AC=α.
∴∠BAB′=∠B′AC =∠C′AC=∠DAC′=α.
∴∠BAD=4α.∵AD∥BC,
∴∠BAD+∠B =180°,即4α+β=180°.
8.B
9.B 【点拨】过点O作OD⊥BC.
∵BC是⊙O的一条弦,BC=6,
∴点O在BC的垂直平分线上,BD=BC=×6=3.
∵AB=AC,
∴点A在BC的垂直平分线上,
∴A,O,D三点共线.
易得∠BAD=∠ABC=45°,
∴AD=BD=3.
又∵OA=1,∴OD=AD-OA=3-1=2.连结OB,
在Rt△OBD中,OB===,
即⊙O的半径为.
10.A 【点拨】如图,作点B关于MN的对称点B′,连结OA,OB,OB′,AB′,易知点B′在⊙O上,当点P为AB′与MN的交点时,PA+PB的值最小,此时PA+PB=PA+PB′=AB′,
∵∠AMN=30°,
∴∠AON=2∠AMN=2×30°=60°.
∵点B为劣弧AN的中点,
∴∠BON=∠AON=×60°=30°.
由轴对称的性质可得∠B′ON=∠BON=30°,
∴∠AOB′=∠AON+∠B′ON=60°+30°=90°.
又∵OA=OB′=1,
∴AB′==,
即PA+PB的最小值为.
二、11.或6
12.30 【点拨】由旋转的性质得AD′=AD=2.
取AD′的中点E,连结BE,
∵AB=1,∠ABD′= 90°,
∴BE=AE=AD′=1=AB,
∴∠BAE=60°,
∴∠DAD′=30°.
13.70
14. - 【点拨】如图,连结AD,AE,取AB的中点F,连结EF.
∵AD==,AB==,
BD==,
∴AD=AB,AD2+AB2=BD2.
∴∠BAD=90°,∴∠ABE=45°.
∵∠ACB=90°,
∴AB是圆弧所在圆的直径,
∴∠AEB=90°,
∴∠BAE=45°.
∵点F为AB的中点,
∴EF=BF=AB=,点F为圆弧所在圆的圆心.
∴∠EFB=2∠BAE=90°,S阴影=S扇形EFB-S△EFB.
∴S阴影=-××=-.
15.30°
16.135; 【点拨】∵AB是半圆O的直径,AB=2 ,∴∠ACB=90°,OA=AB=.
∴∠ABC+∠CAB=90°.
∵点F是的中点,∴=.
∴∠ABF=∠CBF=∠ABC.
∵AD平分∠CAB,
∴∠CAD=∠BAD=∠CAB,
∴∠ABF+∠BAD =(∠ABC+∠CAB)=45°,
∴∠ADB=180°-(∠ABF+∠BAD)=135°.
∴∠ADF=180°-∠ADB=45°.
如图,连结AF,OF,OF交AC于点M,
则OF=OA=.
∵AB是半圆O的直径,
∴∠AFB=90°,
∴∠FAD=45°=∠ADF,
∴AF=DF.
又∵DB=DF,∴BF=2DF=2AF.
在Rt△ABF中,BF2+AF2=AB2,即5AF2=20,∴AF=2.
∵点F是的中点,
∴OF⊥AC,∴∠AMO=∠AMF=90°.
设OM=x,则FM=OF-OM=-x.
在Rt△AOM中,AM2 =OA2-OM2 =()2-x2,
在Rt△AFM中,AM2 =AF2-FM2 =22-(-x)2,
∴()2-x2=22-(-x)2.
解得x=,∴OM=.
∵OF⊥AC,∴点M是AC的中点,
又∵点O是AB的中点,
∴OM是△ABC的中位线,
∴BC=2OM=.
三、17.【证明】∵∠ABD=∠CDB,
∴=, ∴+=+,即=.
∴CD=AB.
18.(1)【证明】∵∠APC=60°,
∴∠ABC=∠APC=60°.
又∵AB=AC,∴△ABC是等边三角形.
(2)【解】由(1)知△ABC是等边三角形,
∴∠ACB=60°.
∵四边形 APBC 是⊙O的内接四边形,
∴∠APB+∠ACB=180°.
∴∠APB=180°-∠ACB=180°-60°=120°.
19.【解】(1) ∵⊙O的弦AB垂直平分半径OC,AB=4 ,
∴AD=BD=AB=2 ,OD=OC.
设⊙O的半径为x,则OC=OA=x,∴OD=x.
在Rt△AOD中,AD2+OD2=OA2,
∴(2 )2+=x2,
解得x1=4,x2=-4(舍去),
∴⊙O的半径是4.
(2)连结BE,由(1)知OA=OE=4,OD=2,
又∵AD=BD,
∴OD是△ABE的中位线,
∴BE=2OD=4.
∵AE是直径,∴∠B=90°,
∴DE===2 .
20. (1)【证明】连结CO,
∵AC∥OD,∴∠A=∠DOB,∠ACO=∠DOC.
∵OA=OC,∴∠A=∠ACO,
∴∠DOB=∠DOC,
∴=,∴点D是的中点.
(2)【解】∵OC=OA=OD=AC=6,
∴△AOC 是等边三角形,
∴∠AOC=60°,
∴S扇形AOC==6π.
过点 C作CE⊥AB于点E,则∠CEO=90°,
∴∠OCE=30°,
∴OE=OC=×6=3.
∴CE==3 ,
∴S△AOC=OA·CE=×6×3 =9 ,
∴S阴影=S扇形AOC-S△AOC=6π-9 .
21. 【证明】(1)如图,连结 BD,
∵=,
∴∠ADB=∠CBD,
∴AD∥BC.
(2)如图,设OC与BD相交于点F.
∵=,OC是⊙O的半径,
∴BC=CD,DF=BF.
又∵∠DFE=∠BFC,∠EDF=∠CBF,
∴△DEF≌△BCF.
∴DE=BC.
∵AD∥BC,∴四边形BCDE是平行四边形.
又∵BC=CD,∴四边形BCDE是菱形.
22. 【解】(1)∵在△ABC 中,AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°.
∵OA=OB,∴∠BAO=∠ABC=30°,
∴∠AOC=∠ABC+∠BAO=60°,
∴∠OAC=90°.
在Rt△OAC中,∠ACB=30°,∴OC=2OA.
∵OA=5,∴OC=10.
(2)如图,连结OD.
∵AD∥BC,
∴∠DAO=∠AOC=60°,
∠DOB=∠ADO.
∵OD=OA,
∴∠ADO=∠DAO=60°.∴∠DOB=60°.
又∵OD=OB,∴△DOB 是等边三角形.
∴BD=OB=OA.
在Rt△OAC 中,OC=2OA,OA2+AC2=OC2,
∴AC=OA=BD,∴=.
23. 【解】如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交于点C,
连结AE,则CF=20 m.
由垂径定理知AF=AB=40 m.
设桥拱所在圆的半径是r m,
在Rt△AFE中,
由勾股定理得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2,解得r=50.
答:桥拱所在圆的半径为50 m.
(2)这艘轮船能顺利通过.
理由如下:如图,假设MN=60 m,且MN∥AB.
连结EM,设EC与MN的交点为D,
∵EC⊥AB,∴DE⊥MN,∴DM=MN=30 m.
∴DE===40(m).
∵EF=EC-CF=50-20=30(m),
∴DF=DE-EF=40-30=10(m).
∵10 m>9 m,∴这艘轮船能顺利通过.
24. 【解】【问题提出】∵∠MAC=∠MBC,
∴∠EAM=180°-∠MAC=180°-∠MBC.
又∵∠BAM=180°-∠MCB,
∴∠EAM=∠BAM.
在△EAM 和△BAM 中,
∴△EAM≌△BAM,
∴ME=MB=MC.
又∵MD⊥AC,∴ED=CD,
∴CD=AE+AD=AB+AD.
【推广运用】1+
【拓展研究】不成立,AD=AB+CD,
理由:如图,延长MD交⊙O于点E,连结EA,EC,EB,
EB交AC于点N.
∵M是的中点,∴=.
∴∠BEM=∠CEM.
在△EDN 和△EDC 中,
∴△EDN≌△EDC,
∴ND=CD,∠END=∠ECD.
又∵∠ECD=∠ABE,∠END=∠ANB,
∴∠ANB=∠ABE,∴AN=AB,
∴AD=AN+ND=AB+CD.
一、选择题(每题3分,共30分)
1.已知⊙O的半径为5 cm,点A是线段OP的中点,当OP=8 cm时,点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O上
C.点A在⊙O内 D.不能确定
2.[2023·宁波余姚市期中]下列事件中,属于必然事件的是( )
A. 三个点确定一个圆
B.每条边都相等的多边形是正多边形
C.平分弦的直径垂直于弦
D.直径所对的圆周角是直角
3.[2023·杭州临平区期中]如图,在同一平面内,将边长相等的正六边形、正方形的一边重合,则∠1的度数为( )
A.18° B.25° C.30° D.45°
4.如图,在4×4的正方形网格中,每个小正方形的边长均为1,若将△ABC绕点A逆时针旋转得到△AB′C′,则的长为( )
A.π B. C.7π D.6π
5.如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是( )
A.4 B.6 C.8 D.10
6.[2023·温州瑞安市期中]如图,四边形ABCD内接于⊙O,点E为上一点,连结BE,DE.若∠A+∠ABC+∠ADC=240°,则∠E=( )
A.55° B.60° C.65° D.70°
7.如图,将菱形ABCD绕点A逆时针旋转α得到菱形AB′C′D′,∠B=β.若AC平分∠B′AC′,则α与β满足的数量关系是( )
A.α=2β B.2α=3β C.4α+β=180° D.3α+2β=180°
8.如图,AB是⊙O的直径,点C,D在⊙O上,且OD经过AC的中点E,连结DC并延长,与AB的延长线相交于点P,若∠CAB=16°,则∠BPC的度数为( )
A.16° B.21° C.32° D.37°
9.如图,⊙O过点B,C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.2 B. C.4 D.3
10.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为劣弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A. B.1 C.2 D.2
二、填空题(每题4分,共24分)
11.[2023·宁波余姚市月考]直角三角形的两边长分别为5和12,则此三角形的外接圆的半径是________.
12.如图,在矩形ABCD中,AB=1,AD=2,将AD绕点A顺时针旋转,点D落在BC上的点D′处,则∠DAD′=________°.
13.如图,A,B,C为⊙O上的点,若∠ACB=20°,则∠BAO的度数为________°.
14.如图,在5×3的网格图中,每个小正方形的边长均为1,设经过格点A,C,B的圆弧与BD交于点E,则阴影部分的面积为__________.(结果保留π)
15.如图,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连结AE.若∠BCD=2∠BAD,则∠DAE的度数是________.
16.[2023·温州龙港市期中]如图,半圆O的直径为AB,AB=2,点C是半圆O上的任意一点,点F是的中点,连结BF交AC于点E,AD平分∠CAB交BF于点D,则∠ADB=________°;当DB=DF时,BC的长为________.
三、解答题(17~19题每题6分,20,21题每题8分,22,23题每题10分,24题12分,共66分)
17.[2023·台州期中]如图,在⊙O中,∠ABD=∠CDB,求证:CD=AB.
18.如图,在⊙O中,已知AB=AC,∠APC=60°.
(1)求证:△ABC是等边三角形.
(2)求∠APB的度数.
19.[2023·宁波余姚市月考]如图,已知⊙O的弦AB垂直平分半径OC,连结AO并延长交⊙O于点E,连结DE,AB=4.
(1)求⊙O的半径.
(2)求DE的长.
20.如图,已知AB是⊙O的直径,弦AC与半径OD平行.
(1)求证:点D是的中点.
(2)若AC=OD=6,求阴影部分的面积.
21.如图,在⊙O中,==,OC与AD相交于点E,连结BE,BC,CD.求证:
(1)AD∥BC.
(2)四边形BCDE为菱形.
22.如图,已知在△ABC中,AB=AC,∠BAC=120°,在BC边上取一点O,以点O为圆心、OB为半径作圆,且⊙O过点A.
(1)若⊙O的半径为5,求线段OC的长.
(2)过点A作AD∥BC交⊙O于点D,连结BD,求的值.
23.如图是一拱形桥,圆弧形桥拱的水面跨度AB=80 m,桥拱到水面的最大高度为20 m.
(1)求桥拱所在圆的半径.
(2)现有一艘宽60 m,顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥,这艘轮船能顺利通过吗?请说明理由.
24.【问题提出】
如图①,AB,AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,求证:CD=AB+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
证明:如图②,延长CA至点E,使AE=AB,连结MA,MB,MC,ME,BC.
∵M是的中点,∴=,
∴∠MCB=∠MBC,MB=MC.(请你在下面的空白处补全小敏的证明过程)
【推广运用】
如图③,等边三角形ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是________.
【拓展研究】
如图④,若将【问题提出】中的“M是的中点”改成“M是的中点”,其余条件不变,“CD=AB+AD”这一结论还成立吗?若成立,请说明理由;若不成立,请写出CD,AB,AD三者之间的数量关系,并说明理由.
INCLUDEPICTURE "../../七八九/4章上.EPS" \* MERGEFORMAT INCLUDEPICTURE "../4章上.EPS" \* MERGEFORMAT \d 答案
一、1.C 2.C 3.A
4.C 【点拨】连结OA,
∵半径OC⊥AB,
∴2AE=AB.
∵OC=5,CE=2,∴OE=3.
在Rt△AOE中,OA=5,
∴AE==4,
∴AB=2AE=8.
5.D 6.B
7.C 【点拨】∵AC平分∠B′AC′,
∴∠B′AC=∠C′AC.
又∵∠BAC=∠DAC,
∴∠BAB′=∠DAC′.
由旋转的性质,得∠BAB′=∠C′AC=α.
∴∠BAB′=∠B′AC =∠C′AC=∠DAC′=α.
∴∠BAD=4α.∵AD∥BC,
∴∠BAD+∠B =180°,即4α+β=180°.
8.B
9.B 【点拨】过点O作OD⊥BC.
∵BC是⊙O的一条弦,BC=6,
∴点O在BC的垂直平分线上,BD=BC=×6=3.
∵AB=AC,
∴点A在BC的垂直平分线上,
∴A,O,D三点共线.
易得∠BAD=∠ABC=45°,
∴AD=BD=3.
又∵OA=1,∴OD=AD-OA=3-1=2.连结OB,
在Rt△OBD中,OB===,
即⊙O的半径为.
10.A 【点拨】如图,作点B关于MN的对称点B′,连结OA,OB,OB′,AB′,易知点B′在⊙O上,当点P为AB′与MN的交点时,PA+PB的值最小,此时PA+PB=PA+PB′=AB′,
∵∠AMN=30°,
∴∠AON=2∠AMN=2×30°=60°.
∵点B为劣弧AN的中点,
∴∠BON=∠AON=×60°=30°.
由轴对称的性质可得∠B′ON=∠BON=30°,
∴∠AOB′=∠AON+∠B′ON=60°+30°=90°.
又∵OA=OB′=1,
∴AB′==,
即PA+PB的最小值为.
二、11.或6
12.30 【点拨】由旋转的性质得AD′=AD=2.
取AD′的中点E,连结BE,
∵AB=1,∠ABD′= 90°,
∴BE=AE=AD′=1=AB,
∴∠BAE=60°,
∴∠DAD′=30°.
13.70
14. - 【点拨】如图,连结AD,AE,取AB的中点F,连结EF.
∵AD==,AB==,
BD==,
∴AD=AB,AD2+AB2=BD2.
∴∠BAD=90°,∴∠ABE=45°.
∵∠ACB=90°,
∴AB是圆弧所在圆的直径,
∴∠AEB=90°,
∴∠BAE=45°.
∵点F为AB的中点,
∴EF=BF=AB=,点F为圆弧所在圆的圆心.
∴∠EFB=2∠BAE=90°,S阴影=S扇形EFB-S△EFB.
∴S阴影=-××=-.
15.30°
16.135; 【点拨】∵AB是半圆O的直径,AB=2 ,∴∠ACB=90°,OA=AB=.
∴∠ABC+∠CAB=90°.
∵点F是的中点,∴=.
∴∠ABF=∠CBF=∠ABC.
∵AD平分∠CAB,
∴∠CAD=∠BAD=∠CAB,
∴∠ABF+∠BAD =(∠ABC+∠CAB)=45°,
∴∠ADB=180°-(∠ABF+∠BAD)=135°.
∴∠ADF=180°-∠ADB=45°.
如图,连结AF,OF,OF交AC于点M,
则OF=OA=.
∵AB是半圆O的直径,
∴∠AFB=90°,
∴∠FAD=45°=∠ADF,
∴AF=DF.
又∵DB=DF,∴BF=2DF=2AF.
在Rt△ABF中,BF2+AF2=AB2,即5AF2=20,∴AF=2.
∵点F是的中点,
∴OF⊥AC,∴∠AMO=∠AMF=90°.
设OM=x,则FM=OF-OM=-x.
在Rt△AOM中,AM2 =OA2-OM2 =()2-x2,
在Rt△AFM中,AM2 =AF2-FM2 =22-(-x)2,
∴()2-x2=22-(-x)2.
解得x=,∴OM=.
∵OF⊥AC,∴点M是AC的中点,
又∵点O是AB的中点,
∴OM是△ABC的中位线,
∴BC=2OM=.
三、17.【证明】∵∠ABD=∠CDB,
∴=, ∴+=+,即=.
∴CD=AB.
18.(1)【证明】∵∠APC=60°,
∴∠ABC=∠APC=60°.
又∵AB=AC,∴△ABC是等边三角形.
(2)【解】由(1)知△ABC是等边三角形,
∴∠ACB=60°.
∵四边形 APBC 是⊙O的内接四边形,
∴∠APB+∠ACB=180°.
∴∠APB=180°-∠ACB=180°-60°=120°.
19.【解】(1) ∵⊙O的弦AB垂直平分半径OC,AB=4 ,
∴AD=BD=AB=2 ,OD=OC.
设⊙O的半径为x,则OC=OA=x,∴OD=x.
在Rt△AOD中,AD2+OD2=OA2,
∴(2 )2+=x2,
解得x1=4,x2=-4(舍去),
∴⊙O的半径是4.
(2)连结BE,由(1)知OA=OE=4,OD=2,
又∵AD=BD,
∴OD是△ABE的中位线,
∴BE=2OD=4.
∵AE是直径,∴∠B=90°,
∴DE===2 .
20. (1)【证明】连结CO,
∵AC∥OD,∴∠A=∠DOB,∠ACO=∠DOC.
∵OA=OC,∴∠A=∠ACO,
∴∠DOB=∠DOC,
∴=,∴点D是的中点.
(2)【解】∵OC=OA=OD=AC=6,
∴△AOC 是等边三角形,
∴∠AOC=60°,
∴S扇形AOC==6π.
过点 C作CE⊥AB于点E,则∠CEO=90°,
∴∠OCE=30°,
∴OE=OC=×6=3.
∴CE==3 ,
∴S△AOC=OA·CE=×6×3 =9 ,
∴S阴影=S扇形AOC-S△AOC=6π-9 .
21. 【证明】(1)如图,连结 BD,
∵=,
∴∠ADB=∠CBD,
∴AD∥BC.
(2)如图,设OC与BD相交于点F.
∵=,OC是⊙O的半径,
∴BC=CD,DF=BF.
又∵∠DFE=∠BFC,∠EDF=∠CBF,
∴△DEF≌△BCF.
∴DE=BC.
∵AD∥BC,∴四边形BCDE是平行四边形.
又∵BC=CD,∴四边形BCDE是菱形.
22. 【解】(1)∵在△ABC 中,AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°.
∵OA=OB,∴∠BAO=∠ABC=30°,
∴∠AOC=∠ABC+∠BAO=60°,
∴∠OAC=90°.
在Rt△OAC中,∠ACB=30°,∴OC=2OA.
∵OA=5,∴OC=10.
(2)如图,连结OD.
∵AD∥BC,
∴∠DAO=∠AOC=60°,
∠DOB=∠ADO.
∵OD=OA,
∴∠ADO=∠DAO=60°.∴∠DOB=60°.
又∵OD=OB,∴△DOB 是等边三角形.
∴BD=OB=OA.
在Rt△OAC 中,OC=2OA,OA2+AC2=OC2,
∴AC=OA=BD,∴=.
23. 【解】如图,设点E是桥拱所在圆的圆心.
过点E作EF⊥AB于点F,延长EF交于点C,
连结AE,则CF=20 m.
由垂径定理知AF=AB=40 m.
设桥拱所在圆的半径是r m,
在Rt△AFE中,
由勾股定理得AE2=AF2+EF2=AF2+(CE-CF)2,
即r2=402+(r-20)2,解得r=50.
答:桥拱所在圆的半径为50 m.
(2)这艘轮船能顺利通过.
理由如下:如图,假设MN=60 m,且MN∥AB.
连结EM,设EC与MN的交点为D,
∵EC⊥AB,∴DE⊥MN,∴DM=MN=30 m.
∴DE===40(m).
∵EF=EC-CF=50-20=30(m),
∴DF=DE-EF=40-30=10(m).
∵10 m>9 m,∴这艘轮船能顺利通过.
24. 【解】【问题提出】∵∠MAC=∠MBC,
∴∠EAM=180°-∠MAC=180°-∠MBC.
又∵∠BAM=180°-∠MCB,
∴∠EAM=∠BAM.
在△EAM 和△BAM 中,
∴△EAM≌△BAM,
∴ME=MB=MC.
又∵MD⊥AC,∴ED=CD,
∴CD=AE+AD=AB+AD.
【推广运用】1+
【拓展研究】不成立,AD=AB+CD,
理由:如图,延长MD交⊙O于点E,连结EA,EC,EB,
EB交AC于点N.
∵M是的中点,∴=.
∴∠BEM=∠CEM.
在△EDN 和△EDC 中,
∴△EDN≌△EDC,
∴ND=CD,∠END=∠ECD.
又∵∠ECD=∠ABE,∠END=∠ANB,
∴∠ANB=∠ABE,∴AN=AB,
∴AD=AN+ND=AB+CD.
同课章节目录
