6.2 反比例函数的图像和性质 (1) 课件(共17张PPT)
文档属性
| 名称 | 6.2 反比例函数的图像和性质 (1) 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 15:32:58 | ||
图片预览





文档简介
(共17张PPT)
6.2 反比例函数的图像和性质(1)
浙教版八年级下册
齐声朗读
一次函数y=kx+b的图象是 __________
一条直线
作一次函数图象时,只要确定_______
两个点
再过这两个点作________就可以了。
直线
作出下列函数的图象:
y= 2x+3
y= -x+6
y= x
y=-x
2
1
-1
-1
2
1
-2
3
5
4
3
5
4
-3
-2
6
O
x
y
●
●
●
y= 2x+3
y= -x+6
y= x
y=-x
一三象限的角平分线
二四象限的角平分线
齐声朗读
一次函数y=kx+b(k ≠ 0)的性质:
(1)与y轴的交点坐标:
(0,b)
当y=0时,
x= ,
.
与 x 轴交点坐标:( ,0)
.
(2)当k>0时,y随x的增大而
增大,
从左往右看,图像上升,呈
“ / ” 。
(3)当k<0时,y随x的增大而
减小,
从左往右看,图像下降,呈
“ \ ” 。
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
>
>
>
<
<
>
<
<
新知讲解
用列表--描点---连线,画出反比例函数 的图象:
x ·· -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 ··
y ·· ··
6
-6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
y=
.
反比例函数
的图像是由两个分支
组成的曲线-----
双曲线
1.当k>0时,图象在一、三象限;
2.当k<0时,图象在二、四象限。
3.图象的两个分支是断开的,关于直角坐标系的原点成中心对称。
新知讲解
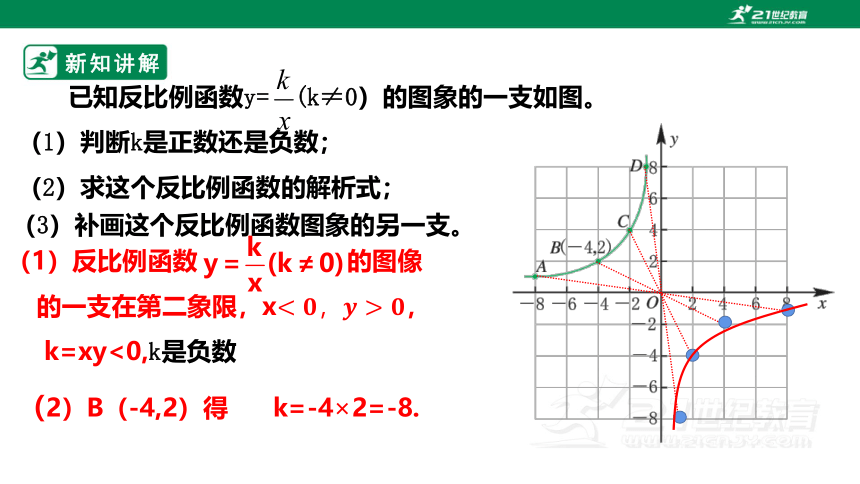
已知反比例函数y= (k≠0)的图象的一支如图。
(1)判断k是正数还是负数;
(2)求这个反比例函数的解析式;
(3)补画这个反比例函数图象的另一支。
(1)反比例函数 的图像
的一支在第二象限,x,
k=xy<0,k是负数
(2)B(-4,2)得 k=-42=-8.
.
归纳总结
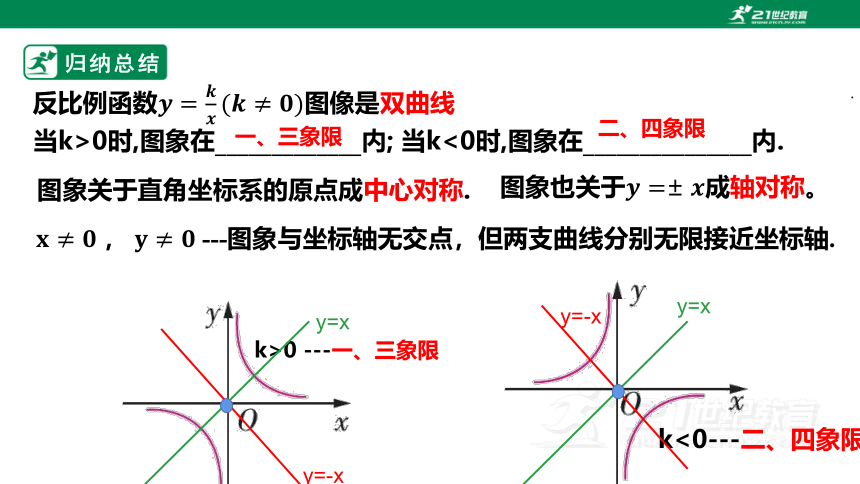
反比例函数图像是双曲线
当k>0时,图象在_____________内; 当k<0时,图象在_______________内.
一、三象限
二、四象限
图象关于直角坐标系的原点成中心对称.
k>0 ---一、三象限
k<0---二、四象限
y=x
y=-x
y=-x
y=x
, ---图象与坐标轴无交点,但两支曲线分别无限接近坐标轴.
图象也关于成轴对称。
.
课堂练习
1. 已知反比例函数y=
.
k=xy=(- )
.
y=
.
(1) 已知反比例函数y=
.
k=xy=()
.
.
.
=( )2
.
=( 2
.
=
.
=
.
变式训练
课堂练习
(2) 已知反比例函数y=
.
k=xy=( )
.
=( )2
.
=( 2
.
=
.
=
.
(3) 已知反比例函数y=
.
k=xy=( )
=( )2
.
=( 2
.
=
.
=
.
变式训练
课堂练习
2.分别根据下列条件判断反比例函数y=
.
(1)图像上一点的坐标为(
π,
)
k=xy=(- )
.
.
(2)与正比例函数y=-4x的图像有公共点
y=-4x
直线y=-4x经过二、四象限
反比例函数y=
.
.
课堂练习
分别根据下列条件判断反比例函数y=
.
(1) k=a2+1
(2) k=a2-2a+3
a2-2a+3=a2-2a+1-1+3
=(a-1)2+2
变式训练-----
.
.
.
.
a2
.
.
a2
.
.
(a+1)2
.
.
(a+1)2
.
.
对二次项、一次项进行配方,常数项撇开
课堂练习
分别根据下列条件判断反比例函数y=
.
(3) k=2a2-4a+13
(4) k=-a2-4a-13
=2【(a2-2a +1) -1】+13
=2(a-1)2 -2+13
=2(a-1)2 +11
2(a-1)2
2(a-1)2 +11
=-(a2+4a)-13
=-(a2+4a+4-4)-13
=-(a-2)2 -9
-(a-2)2
-(a-2)2 -9
变式训练-----
2a2-4a+13=2(a2-2a)+13
.
对二次项、一次项进行配方,常数项撇开
课堂练习
3.反比例函数 y= 的图象与正比例函数 y=2x 的图象
交于点A(1,m),则m= ,反比例函数的解析式为 ,这两个图象的另一个交点坐标是 .
.
2
y=
(-1,-2)
m=2
点A(1,m)既在正比例函数 y=2x 的图象上-------
点A(1,m)又在反比例函数 y= 的图象上-------
k=1
分析:
法1.图象关于直角坐标系的原点成中心对称-----横坐标、纵坐标互为相反数
法2.交点坐标就是方程组的解-------
.
---------
2x=
课堂练习
变式训练
1. 如图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象与
反比例函数 y= 的图象的两个交点,求反比例函数和一次函数的解析式
-4
2
解:(1)∵点A(-4,2)和点B(n,-4)都在反比例函数y=的图象上,
∴ 解得
又∵点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上,
∴ 解得∴y=-,y=-x-2;
.
变式训练
2.已知一次函数y=kx+b的图象与反比例函数 y= 的图象交于
点A(2,3),B(-1,n),求反比例函数和一次函数的解析式
解:∵点A(2,3)和点B(-1,n)都在反比例函数y=的图象上,
∴ 解得
又∵点A(2,3)和点B(-1,-6)都在一次函数y=kx+b的图象上,
∴ 解得∴y=,y=3x-3;
.
课堂练习
我是很长很长的标题
4.已知反比例函数y=
法1:
轴对称-----关于y轴对称、关于x轴对称
法2:
绕点0旋转900-------K型图
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
6.2 反比例函数的图像和性质(1)
浙教版八年级下册
齐声朗读
一次函数y=kx+b的图象是 __________
一条直线
作一次函数图象时,只要确定_______
两个点
再过这两个点作________就可以了。
直线
作出下列函数的图象:
y= 2x+3
y= -x+6
y= x
y=-x
2
1
-1
-1
2
1
-2
3
5
4
3
5
4
-3
-2
6
O
x
y
●
●
●
y= 2x+3
y= -x+6
y= x
y=-x
一三象限的角平分线
二四象限的角平分线
齐声朗读
一次函数y=kx+b(k ≠ 0)的性质:
(1)与y轴的交点坐标:
(0,b)
当y=0时,
x= ,
.
与 x 轴交点坐标:( ,0)
.
(2)当k>0时,y随x的增大而
增大,
从左往右看,图像上升,呈
“ / ” 。
(3)当k<0时,y随x的增大而
减小,
从左往右看,图像下降,呈
“ \ ” 。
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
>
>
>
<
<
>
<
<
新知讲解
用列表--描点---连线,画出反比例函数 的图象:
x ·· -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 ··
y ·· ··
6
-6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
y=
.
反比例函数
的图像是由两个分支
组成的曲线-----
双曲线
1.当k>0时,图象在一、三象限;
2.当k<0时,图象在二、四象限。
3.图象的两个分支是断开的,关于直角坐标系的原点成中心对称。
新知讲解
已知反比例函数y= (k≠0)的图象的一支如图。
(1)判断k是正数还是负数;
(2)求这个反比例函数的解析式;
(3)补画这个反比例函数图象的另一支。
(1)反比例函数 的图像
的一支在第二象限,x,
k=xy<0,k是负数
(2)B(-4,2)得 k=-42=-8.
.
归纳总结
反比例函数图像是双曲线
当k>0时,图象在_____________内; 当k<0时,图象在_______________内.
一、三象限
二、四象限
图象关于直角坐标系的原点成中心对称.
k>0 ---一、三象限
k<0---二、四象限
y=x
y=-x
y=-x
y=x
, ---图象与坐标轴无交点,但两支曲线分别无限接近坐标轴.
图象也关于成轴对称。
.
课堂练习
1. 已知反比例函数y=
.
k=xy=(- )
.
y=
.
(1) 已知反比例函数y=
.
k=xy=()
.
.
.
=( )2
.
=( 2
.
=
.
=
.
变式训练
课堂练习
(2) 已知反比例函数y=
.
k=xy=( )
.
=( )2
.
=( 2
.
=
.
=
.
(3) 已知反比例函数y=
.
k=xy=( )
=( )2
.
=( 2
.
=
.
=
.
变式训练
课堂练习
2.分别根据下列条件判断反比例函数y=
.
(1)图像上一点的坐标为(
π,
)
k=xy=(- )
.
.
(2)与正比例函数y=-4x的图像有公共点
y=-4x
直线y=-4x经过二、四象限
反比例函数y=
.
.
课堂练习
分别根据下列条件判断反比例函数y=
.
(1) k=a2+1
(2) k=a2-2a+3
a2-2a+3=a2-2a+1-1+3
=(a-1)2+2
变式训练-----
.
.
.
.
a2
.
.
a2
.
.
(a+1)2
.
.
(a+1)2
.
.
对二次项、一次项进行配方,常数项撇开
课堂练习
分别根据下列条件判断反比例函数y=
.
(3) k=2a2-4a+13
(4) k=-a2-4a-13
=2【(a2-2a +1) -1】+13
=2(a-1)2 -2+13
=2(a-1)2 +11
2(a-1)2
2(a-1)2 +11
=-(a2+4a)-13
=-(a2+4a+4-4)-13
=-(a-2)2 -9
-(a-2)2
-(a-2)2 -9
变式训练-----
2a2-4a+13=2(a2-2a)+13
.
对二次项、一次项进行配方,常数项撇开
课堂练习
3.反比例函数 y= 的图象与正比例函数 y=2x 的图象
交于点A(1,m),则m= ,反比例函数的解析式为 ,这两个图象的另一个交点坐标是 .
.
2
y=
(-1,-2)
m=2
点A(1,m)既在正比例函数 y=2x 的图象上-------
点A(1,m)又在反比例函数 y= 的图象上-------
k=1
分析:
法1.图象关于直角坐标系的原点成中心对称-----横坐标、纵坐标互为相反数
法2.交点坐标就是方程组的解-------
.
---------
2x=
课堂练习
变式训练
1. 如图,已知A(-4,2),B(n,-4)是一次函数y=kx+b的图象与
反比例函数 y= 的图象的两个交点,求反比例函数和一次函数的解析式
-4
2
解:(1)∵点A(-4,2)和点B(n,-4)都在反比例函数y=的图象上,
∴ 解得
又∵点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上,
∴ 解得∴y=-,y=-x-2;
.
变式训练
2.已知一次函数y=kx+b的图象与反比例函数 y= 的图象交于
点A(2,3),B(-1,n),求反比例函数和一次函数的解析式
解:∵点A(2,3)和点B(-1,n)都在反比例函数y=的图象上,
∴ 解得
又∵点A(2,3)和点B(-1,-6)都在一次函数y=kx+b的图象上,
∴ 解得∴y=,y=3x-3;
.
课堂练习
我是很长很长的标题
4.已知反比例函数y=
法1:
轴对称-----关于y轴对称、关于x轴对称
法2:
绕点0旋转900-------K型图
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
