6.2 反比例函数的图像和性质（2） 课件 (共22张PPT)

(共22张PPT)
6.2 反比例函数的图像和性质（2）
浙教版八年级下册
新知讲解
反比例函数 的图像是由两个分支组成的曲线---
是一种双曲线
1.当k>0时，图象在一、三象限；
当k<0时，图象在二、四象限。
2. 图象的两个分支关于直角坐标系的原点成中心对称。
3.图像不经过原点，它无限接近坐标轴，但永远不与坐标轴相交
齐声朗读
O
k
.
k
O
.
新知导入
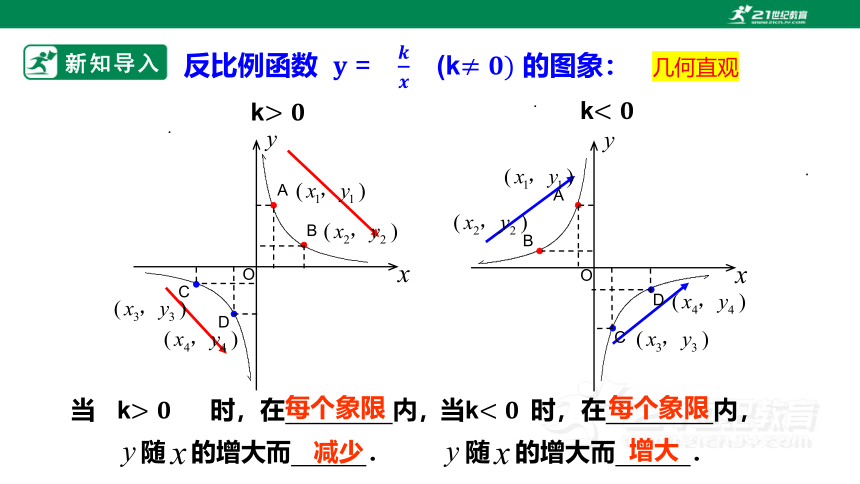
反比例函数　(k 的图象：
.
O
A
B
C
D
当 k时，在　　　 　内，　　
随　的增大而　　　．
每个象限
减少
O
k
.
当k时，在　　　 　内，　　
　随　的增大而　　　．
每个象限
增大
A
B
C
D
几何直观
k
.
新知讲解
O
A
B
C
D
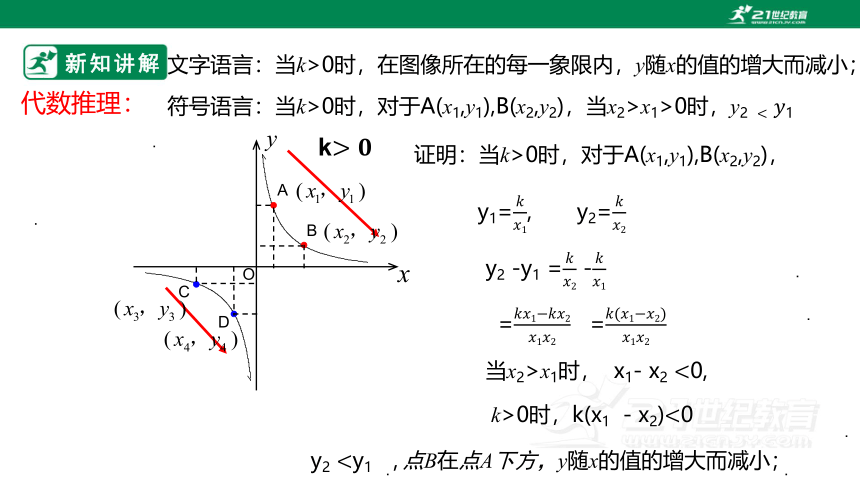
代数推理：
文字语言：当k>0时，在图像所在的每一象限内，y随x的值的增大而减小；
证明：当k>0时，对于A(x1,y1),B(x2,y2)，
y1=, y2=
.
y2 -y1 = -
.
=
=
当x2>x1时， x1- x2 0,
.
k>0时，k(x1 - x2)0
.
符号语言：当k>0时，对于A(x1,y1),B(x2,y2)，当x2>x1>0时，y2
.
y2 y1 , 点B在点A下方，y随x的值的增大而减小；
.
.
k
.
新知讲解
如图，分别在 图象的两个分支上取点 ， ，
易知 ， .
.
.
当 k时，在　　　 　内，　　
随　的增大而　　　．
每个象限
减少
知识小结
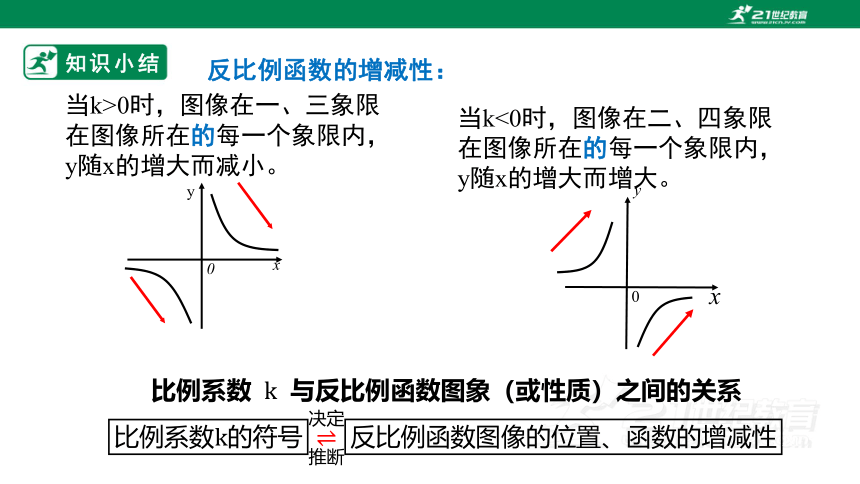
反比例函数的增减性：
当k>0时，图像在一、三象限
在图像所在的每一个象限内，
y随x的增大而减小。
x
y
0
当k<0时，图像在二、四象限
在图像所在的每一个象限内，
y随x的增大而增大。
x
y
0
比例系数 与反比例函数图象（或性质）之间的关系

.
新知讲解
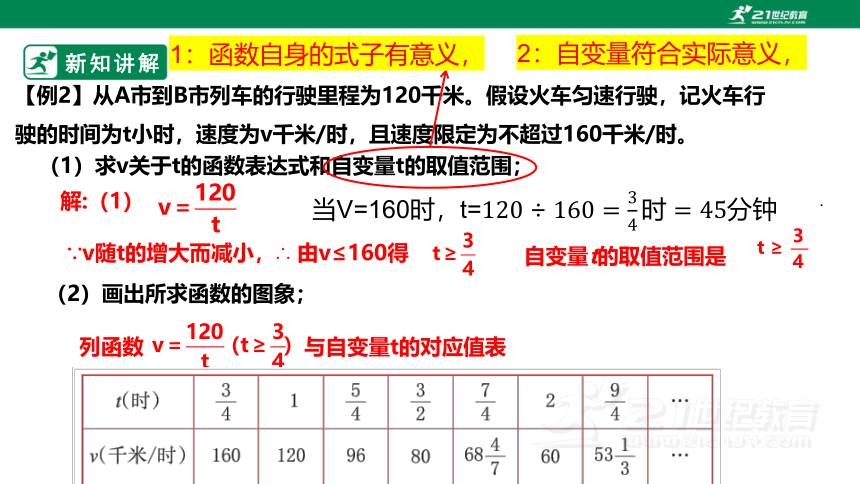
【例2】从A市到B市列车的行驶里程为120千米。假设火车匀速行驶，记火车行驶的时间为t小时，速度为v千米/时，且速度限定为不超过160千米/时。
（1）求v关于t的函数表达式和自变量t的取值范围；
解:（1）
∵v随t的增大而减小，∴ 由v≤160得
自变量t的取值范围是
（2）画出所求函数的图象；
列函数 与自变量t的对应值表
当V=160时，t=
.
1：函数自身的式子有意义，
2：自变量符合实际意义，
新知讲解
不等式是函数的一部分
t
.
V
.
（3）从A市开出一列火车，在40分内（包括40分）到达B市可能吗？；在50分内（包括50分钟）呢？如有可能，那么此时对列车的行驶速度有什么要求？
时=45分钟，火车到B市的最短时间为45分，火车不可能在40分内到达B市.
在50分内到达是有可能的，此时由 得144≤ｖ≤160 （千米/时).
.
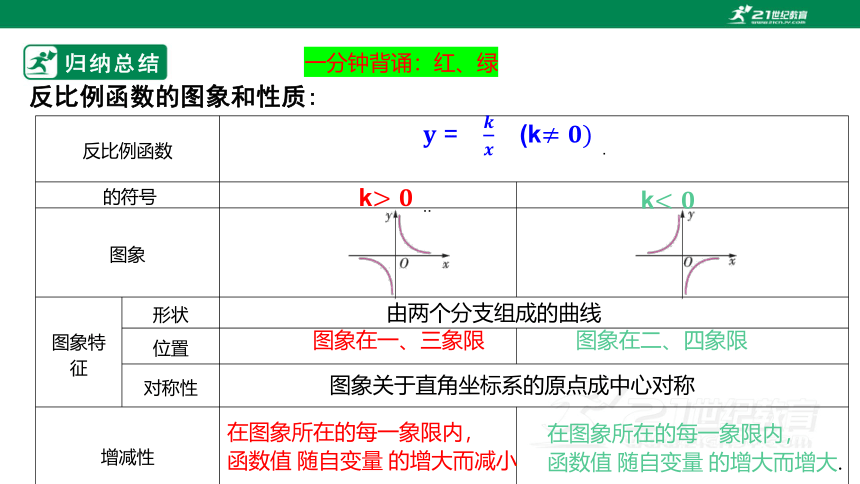
归纳总结
反比例函数的图象和性质:
反比例函数 的符号
图象
图象特 征 形状 位置
对称性 增减性
　(k
.
k
..
k
.
由两个分支组成的曲线
图象在一、三象限
图象在二、四象限
图象关于直角坐标系的原点成中心对称
在图象所在的每一象限内，
函数值 随自变量 的增大而减小
在图象所在的每一象限内，
函数值 随自变量 的增大而增大.
一分钟背诵：红、绿
课堂练习
1.函数 的图象，在每一象限内 y随x的增大而_____.
y =
x
5
增大
2.在双曲线 的一支上， y随x的增大而减小，则m的取值范围是 .
m-2
x
y =
m > 2
m>1
3.已知反比例函数 y= 的图象如图所示，则实数m的取值范围是____
.
课堂练习
4.已知反比例函数y=,则下列结论正确的是 (　　)
A.其图象分别位于第一、三象限
B.当x>0时,y随x的增大而减小
C.若点P(m,n)在它的图象上,则点Q(n,m)也在它的图象上
D.若点A(x1,y1),B(x2,y2)都在该函数图象上,且x1C
课堂练习
5、用“>”或“<”填空：
⑴已知x1，y1和x2，y2是反比例函数 的两对自变量与函数的对应值。若x1画图助你思考
x
y
0
x1
y1
x2
y2
⑵已知x3，y1和x2，y2是反比例函数 的两对自变量与函数的对应值。若x4>x3>0。则0 y4 y3；
x
y
0
x4
y4
x3
y3
.
题型一：同一函数上，比较大小
课堂练习
变式训练
画图助你思考
x
y
0
x1
y1
x2
y2
x3
y3
A
1.已知三个点 ， ， 在反比例函数 的图象上，
其中 ，下列结论中正确的是( )
A. B. C. D.
.
[解析] ∵反比例函数 中， ，∴该函数的图象位于第一、三象限，且
在每一象限内， 随 的增大而减小． ，∴点 ，
在第三象限，点 在第一象限， .
.
课堂练习
变式训练
画图助你思考
x
y
0
2、已知（x1，y1）,（x2，y2） （x3，y3）是反比例函数y= 的图象上的三点，且y1＞y3＞ 0＞y2 ,判断x1 ，x2 ，x3的大小关系
.
x1
y1
x3
y3
x2
y2
xx10x2
.
当k=-2<0时，图像在二、四象限，在图像所在的每一个象限内，
y随x的增大而增大。
课堂练习
变式训练
画图助你思考
x
y
0
3.若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数 y=- (a的图象上,
判断y1,y2,y3的大小关系
.
-1
y1
1
y2
3
y3
y1＞0＞y3 ＞y2
k: “＞”一三，减
口诀：
k: “”二四，增
.
课堂练习
已知一个变量的取值范围，求另一变量的取值范围
<
<
≥
0
x
y
0
画图助你思考
5
1
不等式是函数的一部分
图像不经过原点，它无限接近坐标轴，但永远不与坐标轴相交；
6.已知反比例函数 y = ．
（1）当x＞5时，0　　y 1；
　 （2）当x≤5且x时，则y 　 1,或y＜　　．
.
画图助你思考
不等式是函数的一部分
x
y
0
-9
1.已知反比例函数y=，求 (1)当y≤且y≠0时自变量x的取值范围.
.
变式训练
x≤-9或x>0
注意：两支曲线，各个击破
(2)当y时自变量x的取值范围.
.
-9
.
画图助你思考
不等式是函数的一部分
x
y
0
-3
4
2.已知反比例函数y=，求 (1)当x且x≠0时y 的取值范围.
.
变式训练
注意：两支曲线，各个击破
0.
(2)当x时y 的取值范围.
.
y或y<0
.
x
y
0
画图助你思考
6
1
不等式是函数的一部分
变式训练
3.已知反比例函数y=，求 (1) 当x且x≠0时y 的取值范围.
.
y
.
(2) 当x时y 的取值范围.
.
.
注意：两支曲线，各个击破
记面积为18cm 的平行四边形的一条边长为x（cm），这条边上的高为y（cm）
⑴ 求y关于x的函数解析式，以及自变量x的取值范围。
⑵在如图的直角坐标系内，用描点法画出所求函数的图象；
⑶ 求当边长满足0 < x < 15时，这条边上的高y的取值范围.
2
4
6
8
10
12
14
16
18
20
22
24
26
28
O
2
4
6
8
10
12
14
16
X
y
18
20
22
1.2
(1) y=
x
(2) y1.2
.
图像不经过原点，它无限接近坐标轴，但永远不与坐标轴相交
变式训练
谢谢
21世纪教育网（www.21cnjy.com)
中小学教育资源网站
兼职招聘：
https://www.21cnjy.com/recruitment/home/admin