浙教版九年级上册 第一章 二次函数 复习课课件(共48张PPT)
文档属性
| 名称 | 浙教版九年级上册 第一章 二次函数 复习课课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 599.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 00:00:00 | ||
图片预览








文档简介
(共48张PPT)
二次函数定义
已知函数y=(m2-m)x2+(m-1)x+m+1.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应满足什么条件?
例题讲解
明确起点:明辨a,b,c…
知识链接
知识点 二次函数的定义
一般地,形如 (a,b,c是常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
注意条件:a,b,c限制条件
已知函数y=(m2-m)x2+(m-1)x+m+1.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应满足什么条件?
例题讲解
明确起点:明辨a,b,c…
(1)根据一次函数的定义,得m2-m=0,
解得m=0或m=1,
又m-1≠0,即m≠1.
∴当m=0时,这个函数是一次函数.
(2)根据二次函数的定义,得m2-m≠0,
解得m1≠0,m2≠1.
∴当m≠0且m≠1时,这个函数是二次函数.
方法总结
对于此类题目,应关注二次函数与一次函数的系数特点,比如,对于形如y=ax2+bx+c的函数解析式来说
当a≠0时,该函数是二次函数;
当a=0且b≠0时,该函数是一次函数.
积累经验:学会回到定义去解题…
二次函数y=ax2(a≠0)的图象
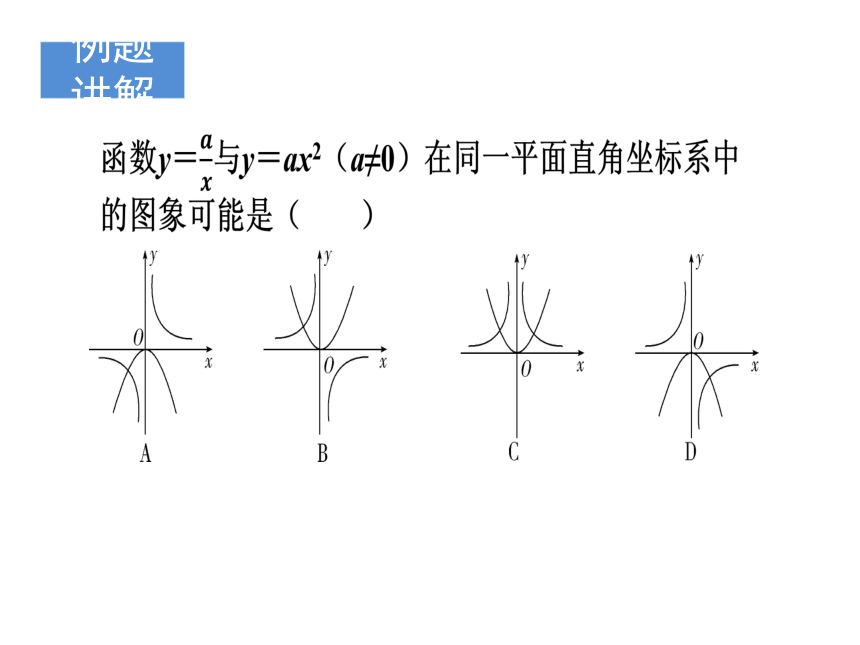
例题讲解
知识链接
本题中可根据a的符号确定反比例函数图象所在象限、二次函数图象开口方向来解决问题.
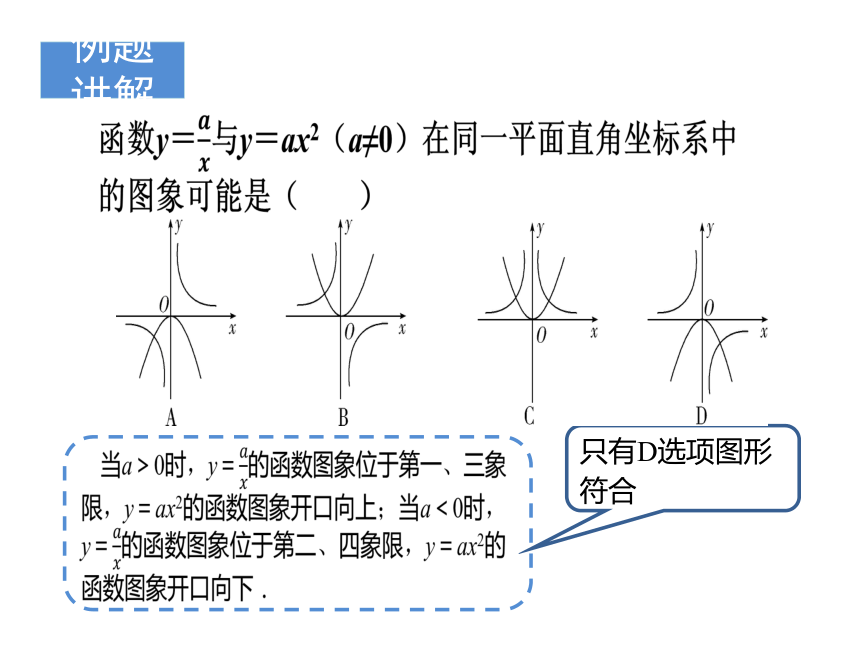
例题讲解
只有D选项图形符合
方法总结
对于这类题目,一般要分类讨论,即讨论a>0与a <0两种情况,然后对各选项运用排除法进行选择,如果有多项都符合,还需要判定两个图象的交点情况.
二次函数y=a(x-m)2+k(a≠0)的图象
例题讲解
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.
先根据题目条件确定函数是一次函数还是二次函数,再
根据函数图象解决问题.
知识链接
知识点 一次函数的图象和二次函数的图象
例题讲解
当k=0时,y=-(x-1)(x+3),所画函数图象如图:
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象;
例题讲解
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(2)根据图象,写出你发现的一条结论;
①图象都过点(1,0)和点(-1,4);
②图象总交x轴于点(1,0);
③k取0和2时的函数图象关于点(0,2)中心对称;④函数y=(x-1)[(k-1)x+(k-3)]的图象都经过
点(1,0)和(-1,4)等等.(答案不唯一)
例题讲解
将函数y2=(x-1)2的图象向左平移4个单位,再向下平移2个单位,得到函数图象的解析式为y3=(x+3)2-2,∴当x=-3时,函数y3的最小值等于-2.
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.
方法总结
函数图象的平移问题,可转化为点的平移,在平移前取函数图象的某些点,确定出平移后对应点的坐标,用待定系数法可求出函数表达式或利用这种方法检验答案是否正确.
二次函数的解析式 王小林
例题讲解
已知二次函数的图象如图所示,求该二次函数的表达式.
(用三种解法回答)
明确起点:从二次函数的图像出发
知识链接
知识点 二次函数的解析式
确定二次函数解析式常用待定系数法,根据条件,可有下列
设立解析式的方法,便于解决问题:
一般式:y=ax2+bx+c
顶点式:y=a(x-h)2+k
两点式:y=a(x-x1)(x-x2)
注意:(a≠0)
(h,k)为顶点...
x1,x2为图像与x轴交点坐标...
例题讲解
已知二次函数的图象如图所示,求该二次函数的表达式.
(用三种解法回答)
明确起点:二次函数图像...
解法一(一般式法):
设所求二次函数的表达式是:
y=ax2+bx+c.
∵二次函数的图象过点(0,3),可求得c=3.
∴二次函数的表达式为y=-x2+2x+3.
(0,3)
(-1,0)
(3,0)
例题讲解
已知二次函数的图象如图所示,求该二次函数的表达式.
(用三种解法回答)
明确起点:二次函数图像...
解法二(顶点式法):
二次函数的图象过点(-1,0),(3,0),可得对称轴为直线x=1,
设所求二次函数的表达式为y=a(x-1)2+k,
∴二次函数的表达式为y=-(x-1)2+4,
即y=-x2+2x+3.
x=1
(-1,0)
(3,0)
例题讲解
已知二次函数的图象如图所示,求该二次函数的表达式.
(用三种解法回答)
解法三(两点式法):
由图可得二次函数的图象与x轴交点为:
(3,0),(0,3),
由两点式设二次函数的表达式为:
y=a(x+1)(x-3).
将(0,3)代入,则有a(0+1)(0-3)=3,
∴a=-1,
∴y=-(x+1)(x-3)=-x2+2x+3.
明确起点:二次函数图像...
(-1,0)
(3,0)
两点式:y=a(x-x1)(x-x2),
x1=-1,x2=3
方法总结
积累经验:学会数形结合去解题…
1、二次函数图象上已知任意三点,
可设一般式y=ax2+bx+c来求解;
2、已知函数图象上的对称点,得到对称轴,
可设顶点式y=a(x-m)2+ k来求解;
3、已知抛物线与x轴的交点坐标,
可设两点式:y=a(x-x1)(x-x2) 来求解.
本题三种解法均可,但是两点式更为便捷.
二次函数的性质-柳凯
例题讲解
如果抛物线y=ax2 + bx+c过定点M(1,1),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式.小敏写出了一个答案:y=2x2+3x-4,请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c+1,求该抛物线顶点纵坐标的值最小时的解析式,请你解答.
确定二次函数解析式常用待定系数法,根据条件,可选取顶点式
便于解决问题:
顶点式:y=a(x-h)2+k 适用于:已知顶点坐标
知识链接
知识点 二次函数的解析式
例题讲解
(1)选择(1,1)为二次函数顶点,令二次项系数为1,
则依据顶点式得:y=(x-1) +1;
写成一般式:y=x -2x+2;
顶点式:y=a(x-h)2+k
如果抛物线y=ax2 + bx+c过定点M(1,1),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式.小敏写出了一个答案:y=2x2+3x-4,请你写出一个不同于小敏的答案;
例题讲解
如果抛物线y=ax2+bx+c过定点M(1,1),则称此抛物线为定点抛物线.
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c+1,求该抛物线顶点纵坐标的值最小时的解析式,请你解答.
积累经验:学会联想顶点式…
(2)∵定点抛物线:y=-x +2bx+c+1=-(x-b) +b +c+1;
∴顶点坐标为(b,b +c+1),且-1+2b+c+1=1,即: c=1-2b;
∵顶点纵坐标:b +c+1=b -2b+2=(b-1) +1,
∴当b=1时,顶点纵坐标最小,此时c=-1;
∴抛物线的解析式为:y=-x +2x.
方法总结
对于此类题目,应关注二次函数的解析式的形式,根据题目中的条件选取最合适的二次函数解析式的形式来解决问题,达到解题的目的。
二次函数最值在实际问题中的应用-高鹏
例题讲解
如图所示是抛物线形状的拱桥.已知水位在AB位置时,水面宽 m水位上升3m就达到警戒线CD,这时水面宽 m .若洪水到来时,水位以每小时0.25m的速度上升,问:过警戒线后几小时将淹到拱桥顶?
建立二次函数模型
通过数学建模,把实际问题转化为二次函数问题:
建立平面直角坐标系,通常以图形的对称轴作为y轴
建立二次函数模型,借助二次函数最值解决实际问题
用配方法或顶点坐标公式求二次函数最值
知识链接
知识点 二次函数的最值在实际问题中的应用
例题讲解
如图所示是抛物线形状的拱桥.已知水位在AB位置时,水面宽 m水位上升3m就达到警戒线CD,这时水面宽 m .若洪水到来时,水位以每小时0.25m的速度上升,问:过警戒线后几小时将淹到拱桥顶?
如图,以AB所在直线为x轴,以AB的中点为原点,建立直角坐标系,则抛物线的顶点M在y轴上,A、B两点的坐标分别为( ,0 ),( ,0 );C、D两点的坐标分别为( ,3),( ,3 ).
例题讲解
设抛物线的函数表达式为 y=ax2+k.
把点B、D的坐标分别代入 y=ax2+k,得 ,解得
∴抛物线的函数表达式为 ,顶点坐标为(0,6).
设CD与y轴交于点N,则 N(0,3). ON=3 m.
∵ OM=6 m, MN=6-3=3(m). 3÷0.25=12(h).
故过警戒线后12h将淹到拱桥顶。
顶点式:y=a(x-h)2+k
方法总结
解决此类问题的关键是要建立直角坐标系,以AB的中点为原点,找出A,B,C,D四点的坐标来确定抛物线的函数表达式.对于此类需要建立坐标系的问题,一般把y轴设定为图形的对称轴.
积累经验:学会建立数学模型解决实际问题···
例题讲解
某批发商以40元/kg的价格购入了某种水果500kg.据市场预测,该种水果的售价y(元/kg)与保存时间x(天)的函数关系式为y=60+2x,但保存这批水果平均每天将损耗10kg,且最多能保存8天.另外,批发商保存该批水果每天还需40元的费用.
(1)若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为 元/kg,获得的总利润为 元;
(2)设批发商将这批水果保存x天后一次性卖出,试求批发商所获得的总利润w(元)与保存时间x(天)之间的函数表达式;
(3)求批发商经营这批水果所能获得的最大利润.
注意条件:x为非负整数
通过数学建模,把实际问题转化为二次函数问题:
利润=售价×销售量-成本
建立二次函数模型,借助二次函数解决实际问题
用配方法或顶点坐标公式并结合实际意义,求出
问题的最大值。
知识链接
知识点 建立二次函数模型解决实际问题
例题讲解
(1)根据题中水果售价(y)与保存时间(x)的函数关系式可知,
当x=1时,y=60+2x=62(元).
利润为:62×(500-10)-40×500-40=10340 (元).
(2)由题意,得w=(60+20x)(500-10x)-40x-500×40= -20x2+360x+10 000.
(3)w= -20x2+360x+10 000= -20(x-9)2 +11 620.
∵0≤x≤8,x为整数,当x≤9时,w随x的增大而增大.
∴当x=8时,w取最大值,w最大=11 600.
积累经验:用配方法求二次函数最大值…
提示:利润=售价×销售量-成本
方法总结
此类问题可根据“利润=售价×销售量-成本”列出函数表达式,利用配方法或顶点坐标公式结合实际情况,即可求出利润的最大值.
积累经验:学会建立数学模型解决实际问题···
二次函数与一元二次方程不等式之间的联系
(2015·咸宁)如图是二次函数y=ax +bx+c的图象,下列结论:①二次三项式ax +bx+c的最大值是4; ②4a+2b+c<0; ③一元二次方程ax +bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数为( )
A.1 B.2 C.3 D.4
训练眼力:从图像你能得到哪些信息?
新 知 链 接
知识点 二次函数的图象
二次函数y=ax +bx+c的图象
(1)a<0开口向下,函数有最大值;a>0开口向上,函数只有最小值
(2)二次函数图象与系数之间的关系(对称轴,特殊点)
(3)二次函数与方程和不等式(组)的关系
(2015·咸宁)如图是二次函数y=ax +bx+c的图象,下列结论:①二次三项式ax +bx+c的最大值是4;
∵开口向下a<0
又∵顶点坐标(-1,4)
∴二次函数y=ax +bx+c最大值为4
即二次三项式ax +bx+c的最大值是4,
故①正确
如图是二次函数y=ax +bx+c的图象,
②4a+2b+c<0;
由图像知:当x=2时,y<0
∴ 4a+2b+c<0,故②正确
2
如图是二次函数y=ax +bx+c的图象,
③一元二次方程ax +bx+c=1的两根之和为-1;
y =1
x = -1
根据抛物线的对称性可知,一元二次方程ax +bx+c=1的两根
满足
∴两根之和为-2,故③错误
如图是二次函数y=ax +bx+c的图象,
④使y≤3成立的x的取值范围是x≥0.其中正确的个数为( )
A.1 B.2 C.3 D.4
y =3
由图像知:使y≤3成立的x的
取值范围是x≤-3或x ≥0
故④错误。所以这题选择B
【方法总结】这种类型的题目主要考查形式为选择题,解决此类题型常用的方法是从二次函数的图象性质出发,通常把已知点坐标代入解析式中找出a,b,c的关系,再结合对称轴方程x= ,确定a、b之间的等量关系,判断与x轴交点情况则利用判别式b -4ac.
二次函数定义
已知函数y=(m2-m)x2+(m-1)x+m+1.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应满足什么条件?
例题讲解
明确起点:明辨a,b,c…
知识链接
知识点 二次函数的定义
一般地,形如 (a,b,c是常数,a≠0)的函数,叫做二次函数.其中,x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.
注意条件:a,b,c限制条件
已知函数y=(m2-m)x2+(m-1)x+m+1.
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是二次函数,则m的值应满足什么条件?
例题讲解
明确起点:明辨a,b,c…
(1)根据一次函数的定义,得m2-m=0,
解得m=0或m=1,
又m-1≠0,即m≠1.
∴当m=0时,这个函数是一次函数.
(2)根据二次函数的定义,得m2-m≠0,
解得m1≠0,m2≠1.
∴当m≠0且m≠1时,这个函数是二次函数.
方法总结
对于此类题目,应关注二次函数与一次函数的系数特点,比如,对于形如y=ax2+bx+c的函数解析式来说
当a≠0时,该函数是二次函数;
当a=0且b≠0时,该函数是一次函数.
积累经验:学会回到定义去解题…
二次函数y=ax2(a≠0)的图象
例题讲解
知识链接
本题中可根据a的符号确定反比例函数图象所在象限、二次函数图象开口方向来解决问题.
例题讲解
只有D选项图形符合
方法总结
对于这类题目,一般要分类讨论,即讨论a>0与a <0两种情况,然后对各选项运用排除法进行选择,如果有多项都符合,还需要判定两个图象的交点情况.
二次函数y=a(x-m)2+k(a≠0)的图象
例题讲解
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象;
(2)根据图象,写出你发现的一条结论;
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.
先根据题目条件确定函数是一次函数还是二次函数,再
根据函数图象解决问题.
知识链接
知识点 一次函数的图象和二次函数的图象
例题讲解
当k=0时,y=-(x-1)(x+3),所画函数图象如图:
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k取0时函数的图象;
例题讲解
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(2)根据图象,写出你发现的一条结论;
①图象都过点(1,0)和点(-1,4);
②图象总交x轴于点(1,0);
③k取0和2时的函数图象关于点(0,2)中心对称;④函数y=(x-1)[(k-1)x+(k-3)]的图象都经过
点(1,0)和(-1,4)等等.(答案不唯一)
例题讲解
将函数y2=(x-1)2的图象向左平移4个单位,再向下平移2个单位,得到函数图象的解析式为y3=(x+3)2-2,∴当x=-3时,函数y3的最小值等于-2.
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(3)将函数y2的图象向左平移4个单位,再向下平移2个单位,得到函数y3的图象,求函数y3的最小值.
方法总结
函数图象的平移问题,可转化为点的平移,在平移前取函数图象的某些点,确定出平移后对应点的坐标,用待定系数法可求出函数表达式或利用这种方法检验答案是否正确.
二次函数的解析式 王小林
例题讲解
已知二次函数的图象如图所示,求该二次函数的表达式.
(用三种解法回答)
明确起点:从二次函数的图像出发
知识链接
知识点 二次函数的解析式
确定二次函数解析式常用待定系数法,根据条件,可有下列
设立解析式的方法,便于解决问题:
一般式:y=ax2+bx+c
顶点式:y=a(x-h)2+k
两点式:y=a(x-x1)(x-x2)
注意:(a≠0)
(h,k)为顶点...
x1,x2为图像与x轴交点坐标...
例题讲解
已知二次函数的图象如图所示,求该二次函数的表达式.
(用三种解法回答)
明确起点:二次函数图像...
解法一(一般式法):
设所求二次函数的表达式是:
y=ax2+bx+c.
∵二次函数的图象过点(0,3),可求得c=3.
∴二次函数的表达式为y=-x2+2x+3.
(0,3)
(-1,0)
(3,0)
例题讲解
已知二次函数的图象如图所示,求该二次函数的表达式.
(用三种解法回答)
明确起点:二次函数图像...
解法二(顶点式法):
二次函数的图象过点(-1,0),(3,0),可得对称轴为直线x=1,
设所求二次函数的表达式为y=a(x-1)2+k,
∴二次函数的表达式为y=-(x-1)2+4,
即y=-x2+2x+3.
x=1
(-1,0)
(3,0)
例题讲解
已知二次函数的图象如图所示,求该二次函数的表达式.
(用三种解法回答)
解法三(两点式法):
由图可得二次函数的图象与x轴交点为:
(3,0),(0,3),
由两点式设二次函数的表达式为:
y=a(x+1)(x-3).
将(0,3)代入,则有a(0+1)(0-3)=3,
∴a=-1,
∴y=-(x+1)(x-3)=-x2+2x+3.
明确起点:二次函数图像...
(-1,0)
(3,0)
两点式:y=a(x-x1)(x-x2),
x1=-1,x2=3
方法总结
积累经验:学会数形结合去解题…
1、二次函数图象上已知任意三点,
可设一般式y=ax2+bx+c来求解;
2、已知函数图象上的对称点,得到对称轴,
可设顶点式y=a(x-m)2+ k来求解;
3、已知抛物线与x轴的交点坐标,
可设两点式:y=a(x-x1)(x-x2) 来求解.
本题三种解法均可,但是两点式更为便捷.
二次函数的性质-柳凯
例题讲解
如果抛物线y=ax2 + bx+c过定点M(1,1),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式.小敏写出了一个答案:y=2x2+3x-4,请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c+1,求该抛物线顶点纵坐标的值最小时的解析式,请你解答.
确定二次函数解析式常用待定系数法,根据条件,可选取顶点式
便于解决问题:
顶点式:y=a(x-h)2+k 适用于:已知顶点坐标
知识链接
知识点 二次函数的解析式
例题讲解
(1)选择(1,1)为二次函数顶点,令二次项系数为1,
则依据顶点式得:y=(x-1) +1;
写成一般式:y=x -2x+2;
顶点式:y=a(x-h)2+k
如果抛物线y=ax2 + bx+c过定点M(1,1),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式.小敏写出了一个答案:y=2x2+3x-4,请你写出一个不同于小敏的答案;
例题讲解
如果抛物线y=ax2+bx+c过定点M(1,1),则称此抛物线为定点抛物线.
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c+1,求该抛物线顶点纵坐标的值最小时的解析式,请你解答.
积累经验:学会联想顶点式…
(2)∵定点抛物线:y=-x +2bx+c+1=-(x-b) +b +c+1;
∴顶点坐标为(b,b +c+1),且-1+2b+c+1=1,即: c=1-2b;
∵顶点纵坐标:b +c+1=b -2b+2=(b-1) +1,
∴当b=1时,顶点纵坐标最小,此时c=-1;
∴抛物线的解析式为:y=-x +2x.
方法总结
对于此类题目,应关注二次函数的解析式的形式,根据题目中的条件选取最合适的二次函数解析式的形式来解决问题,达到解题的目的。
二次函数最值在实际问题中的应用-高鹏
例题讲解
如图所示是抛物线形状的拱桥.已知水位在AB位置时,水面宽 m水位上升3m就达到警戒线CD,这时水面宽 m .若洪水到来时,水位以每小时0.25m的速度上升,问:过警戒线后几小时将淹到拱桥顶?
建立二次函数模型
通过数学建模,把实际问题转化为二次函数问题:
建立平面直角坐标系,通常以图形的对称轴作为y轴
建立二次函数模型,借助二次函数最值解决实际问题
用配方法或顶点坐标公式求二次函数最值
知识链接
知识点 二次函数的最值在实际问题中的应用
例题讲解
如图所示是抛物线形状的拱桥.已知水位在AB位置时,水面宽 m水位上升3m就达到警戒线CD,这时水面宽 m .若洪水到来时,水位以每小时0.25m的速度上升,问:过警戒线后几小时将淹到拱桥顶?
如图,以AB所在直线为x轴,以AB的中点为原点,建立直角坐标系,则抛物线的顶点M在y轴上,A、B两点的坐标分别为( ,0 ),( ,0 );C、D两点的坐标分别为( ,3),( ,3 ).
例题讲解
设抛物线的函数表达式为 y=ax2+k.
把点B、D的坐标分别代入 y=ax2+k,得 ,解得
∴抛物线的函数表达式为 ,顶点坐标为(0,6).
设CD与y轴交于点N,则 N(0,3). ON=3 m.
∵ OM=6 m, MN=6-3=3(m). 3÷0.25=12(h).
故过警戒线后12h将淹到拱桥顶。
顶点式:y=a(x-h)2+k
方法总结
解决此类问题的关键是要建立直角坐标系,以AB的中点为原点,找出A,B,C,D四点的坐标来确定抛物线的函数表达式.对于此类需要建立坐标系的问题,一般把y轴设定为图形的对称轴.
积累经验:学会建立数学模型解决实际问题···
例题讲解
某批发商以40元/kg的价格购入了某种水果500kg.据市场预测,该种水果的售价y(元/kg)与保存时间x(天)的函数关系式为y=60+2x,但保存这批水果平均每天将损耗10kg,且最多能保存8天.另外,批发商保存该批水果每天还需40元的费用.
(1)若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为 元/kg,获得的总利润为 元;
(2)设批发商将这批水果保存x天后一次性卖出,试求批发商所获得的总利润w(元)与保存时间x(天)之间的函数表达式;
(3)求批发商经营这批水果所能获得的最大利润.
注意条件:x为非负整数
通过数学建模,把实际问题转化为二次函数问题:
利润=售价×销售量-成本
建立二次函数模型,借助二次函数解决实际问题
用配方法或顶点坐标公式并结合实际意义,求出
问题的最大值。
知识链接
知识点 建立二次函数模型解决实际问题
例题讲解
(1)根据题中水果售价(y)与保存时间(x)的函数关系式可知,
当x=1时,y=60+2x=62(元).
利润为:62×(500-10)-40×500-40=10340 (元).
(2)由题意,得w=(60+20x)(500-10x)-40x-500×40= -20x2+360x+10 000.
(3)w= -20x2+360x+10 000= -20(x-9)2 +11 620.
∵0≤x≤8,x为整数,当x≤9时,w随x的增大而增大.
∴当x=8时,w取最大值,w最大=11 600.
积累经验:用配方法求二次函数最大值…
提示:利润=售价×销售量-成本
方法总结
此类问题可根据“利润=售价×销售量-成本”列出函数表达式,利用配方法或顶点坐标公式结合实际情况,即可求出利润的最大值.
积累经验:学会建立数学模型解决实际问题···
二次函数与一元二次方程不等式之间的联系
(2015·咸宁)如图是二次函数y=ax +bx+c的图象,下列结论:①二次三项式ax +bx+c的最大值是4; ②4a+2b+c<0; ③一元二次方程ax +bx+c=1的两根之和为-1;④使y≤3成立的x的取值范围是x≥0.其中正确的个数为( )
A.1 B.2 C.3 D.4
训练眼力:从图像你能得到哪些信息?
新 知 链 接
知识点 二次函数的图象
二次函数y=ax +bx+c的图象
(1)a<0开口向下,函数有最大值;a>0开口向上,函数只有最小值
(2)二次函数图象与系数之间的关系(对称轴,特殊点)
(3)二次函数与方程和不等式(组)的关系
(2015·咸宁)如图是二次函数y=ax +bx+c的图象,下列结论:①二次三项式ax +bx+c的最大值是4;
∵开口向下a<0
又∵顶点坐标(-1,4)
∴二次函数y=ax +bx+c最大值为4
即二次三项式ax +bx+c的最大值是4,
故①正确
如图是二次函数y=ax +bx+c的图象,
②4a+2b+c<0;
由图像知:当x=2时,y<0
∴ 4a+2b+c<0,故②正确
2
如图是二次函数y=ax +bx+c的图象,
③一元二次方程ax +bx+c=1的两根之和为-1;
y =1
x = -1
根据抛物线的对称性可知,一元二次方程ax +bx+c=1的两根
满足
∴两根之和为-2,故③错误
如图是二次函数y=ax +bx+c的图象,
④使y≤3成立的x的取值范围是x≥0.其中正确的个数为( )
A.1 B.2 C.3 D.4
y =3
由图像知:使y≤3成立的x的
取值范围是x≤-3或x ≥0
故④错误。所以这题选择B
【方法总结】这种类型的题目主要考查形式为选择题,解决此类题型常用的方法是从二次函数的图象性质出发,通常把已知点坐标代入解析式中找出a,b,c的关系,再结合对称轴方程x= ,确定a、b之间的等量关系,判断与x轴交点情况则利用判别式b -4ac.
同课章节目录
