第六章 反比例函数章末复习-----反比例函数k 的几何意义 课件(共27张PPT)
文档属性
| 名称 | 第六章 反比例函数章末复习-----反比例函数k 的几何意义 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-25 19:19:10 | ||
图片预览


文档简介
(共27张PPT)
浙教版八年级下册
第六章 反比例函数 章末复习
-----比例系数k的几何意义
新知导入
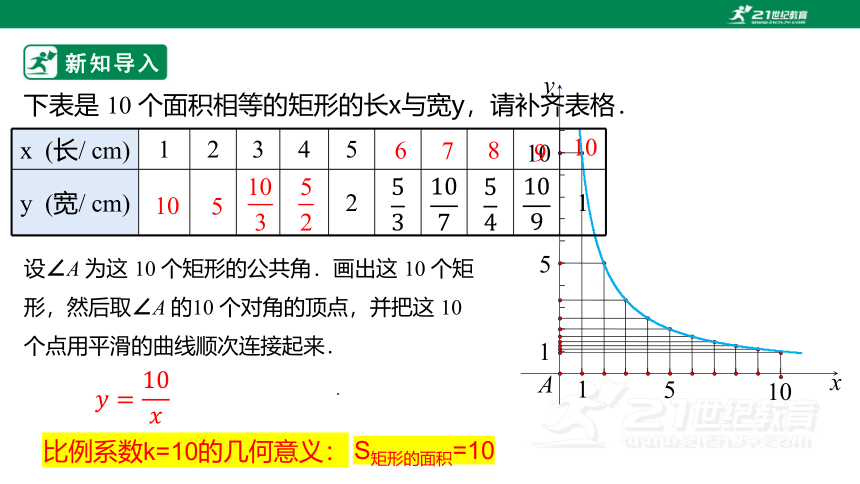
设∠A 为这 10 个矩形的公共角.画出这 10 个矩形,然后取∠A 的10 个对角的顶点,并把这 10 个点用平滑的曲线顺次连接起来.
1
A
x
y
5
10
5
10
1
下表是 10 个面积相等的矩形的长x与宽y,请补齐表格.
x (长/ cm) 1 2 3 4 5
y (宽/ cm) 2 1
10
5
6
7
8
9
10
比例系数k=10的几何意义:
S矩形的面积=10
.
yy
yx
0
P
yPA
yPB
yy
yx
0
yPP
yPA
B
新知讲解
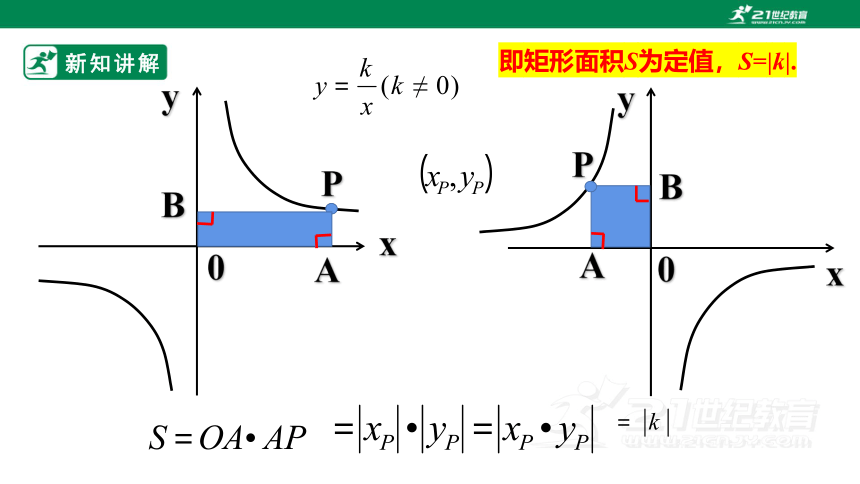
即矩形面积S为定值,S=|k|.
齐声朗读
K的几何意义1: 过双曲线上任意一点,向两坐标轴作垂线,
两条垂线与坐标轴所围成的矩形的面积为常数 |k|.
k 的代数意义:双曲线上任意一点 (x,y) 的两坐标之积为常数K---
即xy=k
x
y
O
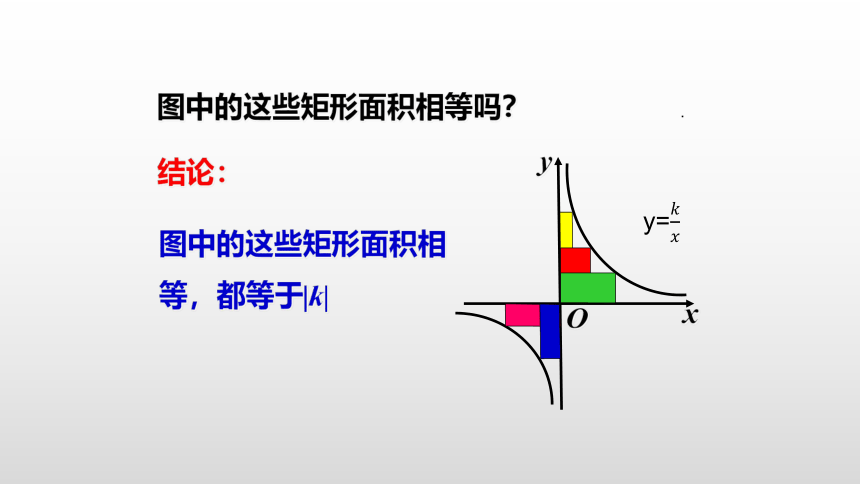
图中的这些矩形面积相等,都等于|k|
结论:
图中的这些矩形面积相等吗?
y=
.
新知讲解
P(m,n)
A
O
y
x
A
O
y
x
P(m,n)
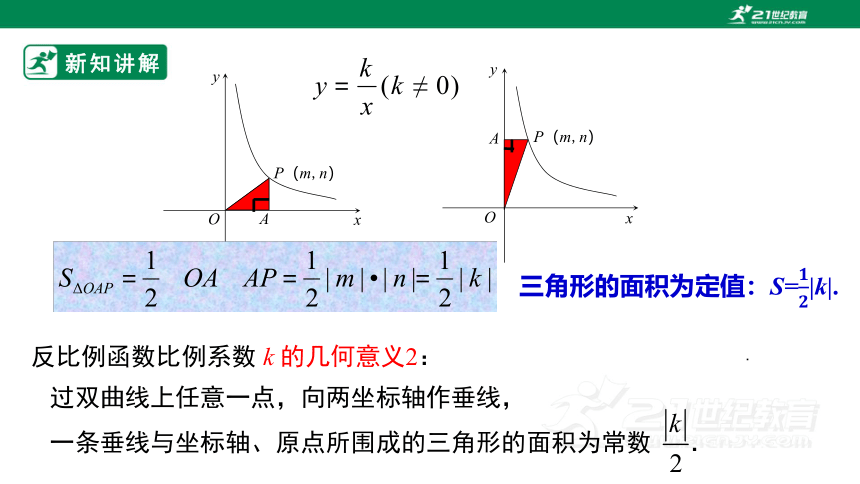
反比例函数比例系数 k 的几何意义2:
过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积为常数 .
三角形的面积为定值:S=|k|.
.
x
y
O
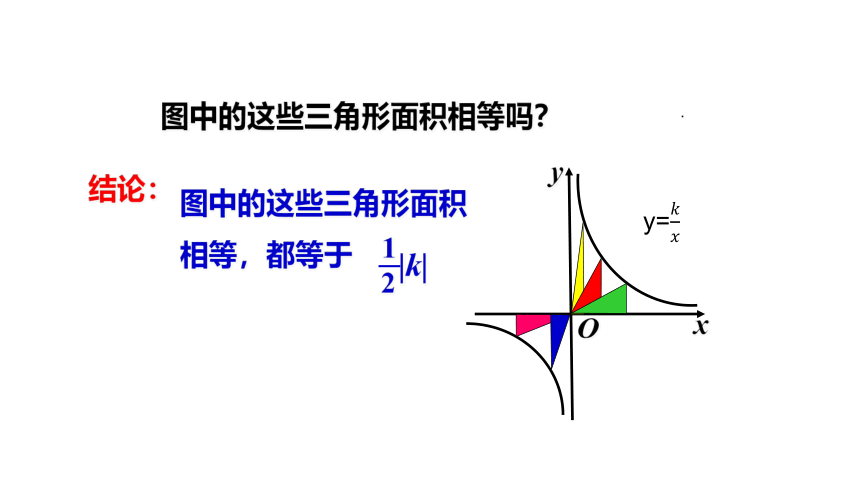
图中的这些三角形面积相等,都等于
结论:
图中的这些三角形面积相等吗?
|k|
1
2
y=
.
新知导入
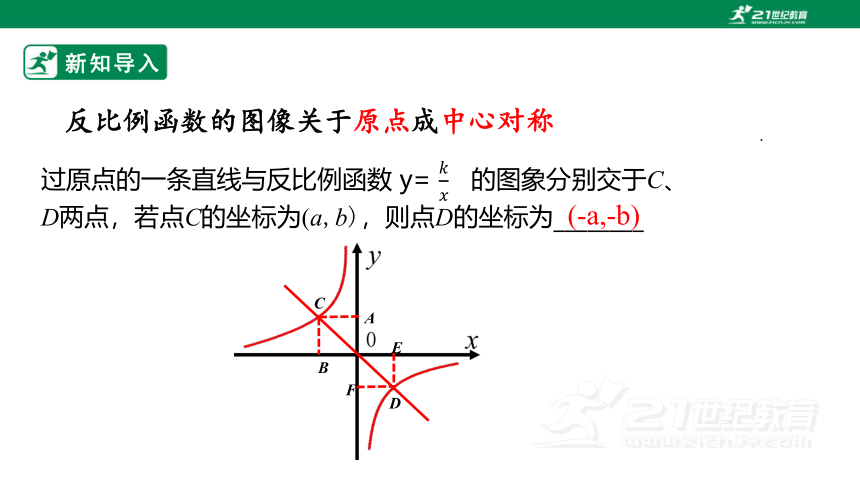
反比例函数的图像关于原点成中心对称
(-a,-b)
C
D
A
B
E
F
过原点的一条直线与反比例函数 y= 的图象分别交于C、
D两点,若点C的坐标为(a,b),则点D的坐标为________
.
yy
yx
0
A
D
B
C
yy
yx
0
A
B
C
D
新知讲解
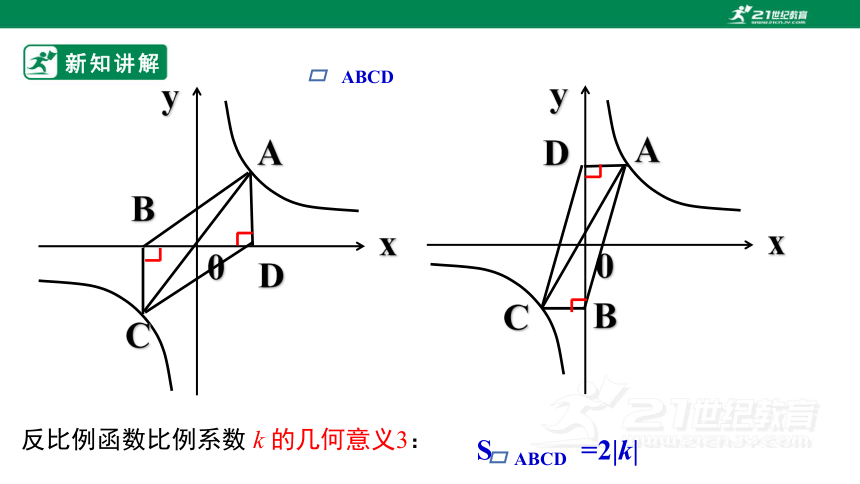
反比例函数比例系数 k 的几何意义3:
S ABCD =2|k|
ABCD
yy
yx
0
yy
yx
0
S=2|k|
S=|k|
新知讲解
k 的几何意义4:
k 的几何意义5:
如图,点A是反比例函数y= 图象上一点,过点A作AB⊥y轴于点B,
点C、D在x轴上,且BC∥AD
新知讲解
k 的几何意义6:
S ABCD =|k|
E
课堂练习
1.反比例函数y= - 的图像上有一点E,过点 E 作 EP⊥ y 轴于点P,则△EOP的面积为________.
2.反比例函数y= - 的图像上有一点E,过点E作EP⊥ y轴于点P,若在x轴上任意取一点F,则△EPF的面积为_________.
1
1
平行造等积
3.如图,点A,点B分别在两条不同的双曲线上,且AB∥x轴,点C和点D在x轴上,若四边形ABCD为矩形,则矩形ABCD的面积为___________
3
课堂练习
课堂练习
4.平行四边形ABCD的顶点A在反比例函数 y= - 的图像上,AB∥x轴交y轴于点B,CD在x轴上任意移动,则四边形ABDC的面积是
C’
6
板书设计
5.如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为3,则这个反比例函数的解析式为 .
同底等高的两个三角形的面积相等.
O
A
x
y
B
P
y=
.
课堂总结
5.如图,已知点A在反比例函数的图象上,AB⊥x轴于点B,点C为y轴上的一点,若△ABC的面积是3,则反比例函数的解析式为______.
O
A
x
y
B
C
y=
6
x
课堂练习
-20
课堂练习
7.已知点A、B分别在反比例函数 、
的图像上 ,AB∥x轴,点F在x轴上任意移动,则△ABF的面积是
y= -
y=
O
B
A
C
F
y
x
5
课堂练习
8.如图,点A、点B分别在反比例函数y= 和y= 的图象上,且AB//x 轴,求△OAB的面积。
A
B
O
x
y
A
B
O
x
y
1
课堂练习
9.如图,设点P在函数 y= 的图象上,PC⊥x轴于点C,交函数y= 的图象于点A,PD⊥y轴于点D,交函数y= 的图象于点B,则四边形PAOB的面积为 .
x
y
B
P
D
A
C
O
6-2=4
课堂练习
B
A
O
C
y
x
D
10.如图所示,在平面直角坐标系中,菱形OABC的面积为8,点B在y轴上,点C在反比例函数 的图象上,求k的值
.
解析:连接AC交OB于D,如图,
∵四边形ABCO为菱形,
∴AC⊥OB,S△OCD=S菱形ABCO=×8=2,
∵CD⊥y轴,∴S△OCD=|k|,即|k|=2,
而k<0,∴k=-4.
.
11.如图,过反比例函数 图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,⊿AOE与梯形ECDB的面积分别为 S1 、S2,比较它们的大小,可得 ( )
A.S1>S2 B.S1=S2
C.S1< S2 D.S1和S2的大小关系不确定
B
课堂练习
课堂练习
等积藏其中
图象在二、四象,
11. 如图,点P,点Q都在反比例函数y=的图象上,过点P分别作x轴、y轴的垂线,两条垂线与两坐标轴围成的矩形面积为S1,过点Q作x轴的垂线,交x轴于点A,△0AQ的面积为S2,若S1+S2=3,求K的值
.
课堂练习
12. 如图,双曲线y=- (x<0) 经过 ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则 ABCO的面积是( )
B.
A.
C. 3
D. 6
.
课堂练习
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版八年级下册
第六章 反比例函数 章末复习
-----比例系数k的几何意义
新知导入
设∠A 为这 10 个矩形的公共角.画出这 10 个矩形,然后取∠A 的10 个对角的顶点,并把这 10 个点用平滑的曲线顺次连接起来.
1
A
x
y
5
10
5
10
1
下表是 10 个面积相等的矩形的长x与宽y,请补齐表格.
x (长/ cm) 1 2 3 4 5
y (宽/ cm) 2 1
10
5
6
7
8
9
10
比例系数k=10的几何意义:
S矩形的面积=10
.
yy
yx
0
P
yPA
yPB
yy
yx
0
yPP
yPA
B
新知讲解
即矩形面积S为定值,S=|k|.
齐声朗读
K的几何意义1: 过双曲线上任意一点,向两坐标轴作垂线,
两条垂线与坐标轴所围成的矩形的面积为常数 |k|.
k 的代数意义:双曲线上任意一点 (x,y) 的两坐标之积为常数K---
即xy=k
x
y
O
图中的这些矩形面积相等,都等于|k|
结论:
图中的这些矩形面积相等吗?
y=
.
新知讲解
P(m,n)
A
O
y
x
A
O
y
x
P(m,n)
反比例函数比例系数 k 的几何意义2:
过双曲线上任意一点,向两坐标轴作垂线,
一条垂线与坐标轴、原点所围成的三角形的面积为常数 .
三角形的面积为定值:S=|k|.
.
x
y
O
图中的这些三角形面积相等,都等于
结论:
图中的这些三角形面积相等吗?
|k|
1
2
y=
.
新知导入
反比例函数的图像关于原点成中心对称
(-a,-b)
C
D
A
B
E
F
过原点的一条直线与反比例函数 y= 的图象分别交于C、
D两点,若点C的坐标为(a,b),则点D的坐标为________
.
yy
yx
0
A
D
B
C
yy
yx
0
A
B
C
D
新知讲解
反比例函数比例系数 k 的几何意义3:
S ABCD =2|k|
ABCD
yy
yx
0
yy
yx
0
S=2|k|
S=|k|
新知讲解
k 的几何意义4:
k 的几何意义5:
如图,点A是反比例函数y= 图象上一点,过点A作AB⊥y轴于点B,
点C、D在x轴上,且BC∥AD
新知讲解
k 的几何意义6:
S ABCD =|k|
E
课堂练习
1.反比例函数y= - 的图像上有一点E,过点 E 作 EP⊥ y 轴于点P,则△EOP的面积为________.
2.反比例函数y= - 的图像上有一点E,过点E作EP⊥ y轴于点P,若在x轴上任意取一点F,则△EPF的面积为_________.
1
1
平行造等积
3.如图,点A,点B分别在两条不同的双曲线上,且AB∥x轴,点C和点D在x轴上,若四边形ABCD为矩形,则矩形ABCD的面积为___________
3
课堂练习
课堂练习
4.平行四边形ABCD的顶点A在反比例函数 y= - 的图像上,AB∥x轴交y轴于点B,CD在x轴上任意移动,则四边形ABDC的面积是
C’
6
板书设计
5.如图,A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为3,则这个反比例函数的解析式为 .
同底等高的两个三角形的面积相等.
O
A
x
y
B
P
y=
.
课堂总结
5.如图,已知点A在反比例函数的图象上,AB⊥x轴于点B,点C为y轴上的一点,若△ABC的面积是3,则反比例函数的解析式为______.
O
A
x
y
B
C
y=
6
x
课堂练习
-20
课堂练习
7.已知点A、B分别在反比例函数 、
的图像上 ,AB∥x轴,点F在x轴上任意移动,则△ABF的面积是
y= -
y=
O
B
A
C
F
y
x
5
课堂练习
8.如图,点A、点B分别在反比例函数y= 和y= 的图象上,且AB//x 轴,求△OAB的面积。
A
B
O
x
y
A
B
O
x
y
1
课堂练习
9.如图,设点P在函数 y= 的图象上,PC⊥x轴于点C,交函数y= 的图象于点A,PD⊥y轴于点D,交函数y= 的图象于点B,则四边形PAOB的面积为 .
x
y
B
P
D
A
C
O
6-2=4
课堂练习
B
A
O
C
y
x
D
10.如图所示,在平面直角坐标系中,菱形OABC的面积为8,点B在y轴上,点C在反比例函数 的图象上,求k的值
.
解析:连接AC交OB于D,如图,
∵四边形ABCO为菱形,
∴AC⊥OB,S△OCD=S菱形ABCO=×8=2,
∵CD⊥y轴,∴S△OCD=|k|,即|k|=2,
而k<0,∴k=-4.
.
11.如图,过反比例函数 图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连结OA、OB,设AC与OB的交点为E,⊿AOE与梯形ECDB的面积分别为 S1 、S2,比较它们的大小,可得 ( )
A.S1>S2 B.S1=S2
C.S1< S2 D.S1和S2的大小关系不确定
B
课堂练习
课堂练习
等积藏其中
图象在二、四象,
11. 如图,点P,点Q都在反比例函数y=的图象上,过点P分别作x轴、y轴的垂线,两条垂线与两坐标轴围成的矩形面积为S1,过点Q作x轴的垂线,交x轴于点A,△0AQ的面积为S2,若S1+S2=3,求K的值
.
课堂练习
12. 如图,双曲线y=- (x<0) 经过 ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则 ABCO的面积是( )
B.
A.
C. 3
D. 6
.
课堂练习
C
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
