浙教版八年级上册 2.6 直角三角形 作业设计练习 含答案
文档属性
| 名称 | 浙教版八年级上册 2.6 直角三角形 作业设计练习 含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 976.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-26 10:49:00 | ||
图片预览


文档简介
《直角三角形》作业设计
一、作业目标
1.巩固直角三角形的性质及判定,会判断一个三角形是直角三角形,会运用直角三角形的性质解决有关图形的论证、计算等问题。
2.熟练掌握勾股定理并运用勾股定理解决几何问题,会利用勾股定理的逆定理判定一个三角形为直角三角形。
3.巩固判定两个直角三角形全等的方法,用利用角平分线的定理与逆定理解决几何问题。
4.利用类比的方法,让学会学会探究新问题,体验数学的应用价值及学习成就感。
二、使用建议
建议学生学习完浙教版八上2.6,2.7,2.8后使用或八上第二章学习完后使用。
三、作业呈现
(一)立足基础
1.已知△ABC的三边为,具备下列条件的△ABC,不是直角三角形的是( )
A.∠A﹣∠B=∠C B.
C.∠A:∠B:∠C=3:4:5 D.
2.如图,某社会实践学习小组为测量学校A与河对岸江景房B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=30米.由此可求得学校与江景房之间的距离AB等于( )
A.15米 B.60米 C.80米 D.120米
3.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,添加一个条件,不能使得
Rt△ABC≌Rt△DCB的是( )
A.AB=DC B.AC=DB C.∠ABC=∠DCB D.BC=BD
(第2题) (第3题)
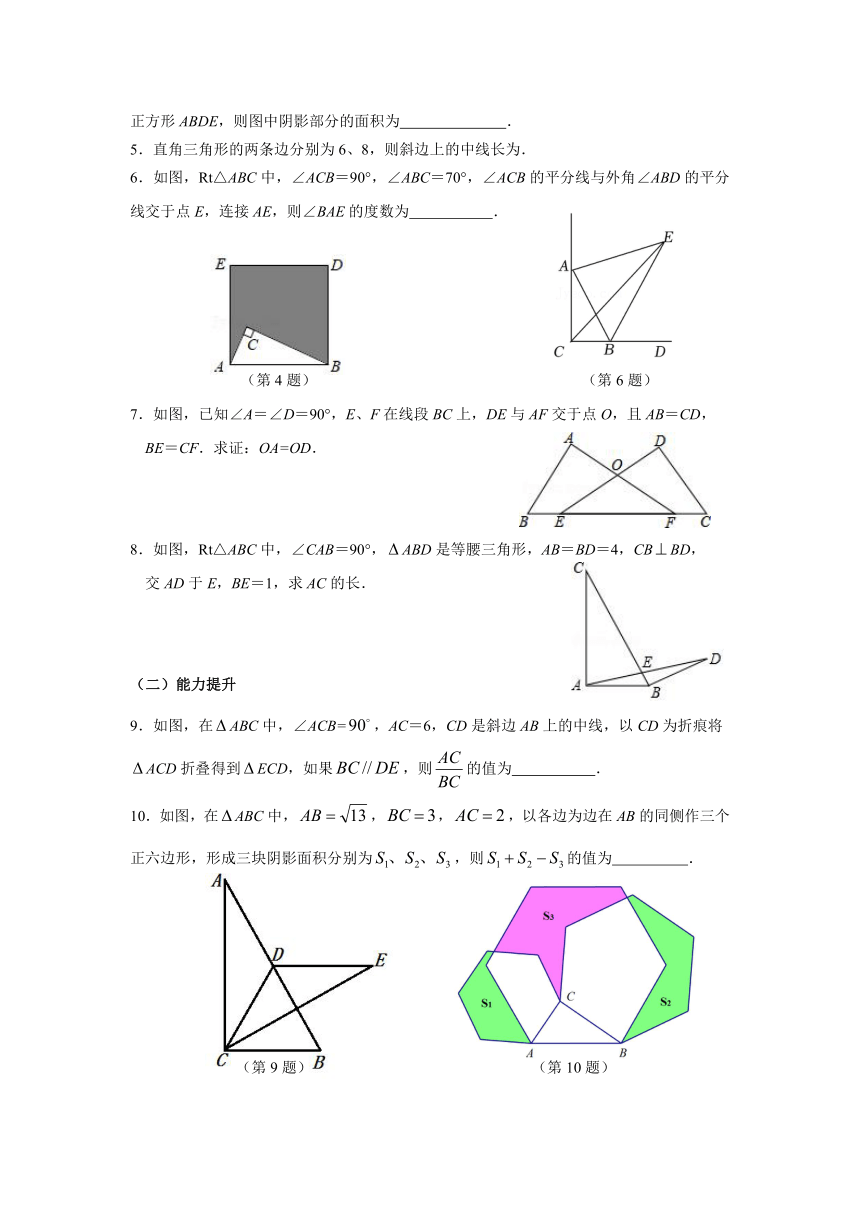
4.如图,在ABC中,∠C=90°,AC=4cm,BC=9cm.以AB为一边在ABC的同侧作正方形ABDE,则图中阴影部分的面积为 .
5.直角三角形的两条边分别为6、8,则斜边上的中线长为.
6.如图,Rt△ABC中,∠ACB=90°,∠ABC=70°,∠ACB的平分线与外角∠ABD的平分线交于点E,连接AE,则∠BAE的度数为 .
(第4题) (第6题)
7.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,
BE=CF.求证:OA=OD.
8.如图,Rt△ABC中,∠CAB=90°,ABD是等腰三角形,AB=BD=4,CBBD,
交AD于E,BE=1,求AC的长.
(二)能力提升
9.如图,在ABC中,∠ACB=,AC=6,CD是斜边AB上的中线,以CD为折痕将
ACD折叠得到ECD,如果,则的值为 .
10.如图,在ABC中,,,,以各边为边在AB的同侧作三个正六边形,形成三块阴影面积分别为,则的值为 .
(第9题) (第10题)
11.定义:如果三角形的两个内角与满足,那么我们称这样的三角形为“奇妙三角形”.若一个直角三角形是“奇妙三角形”,它的较短直角边长为1,则它的较长直角边长为 .
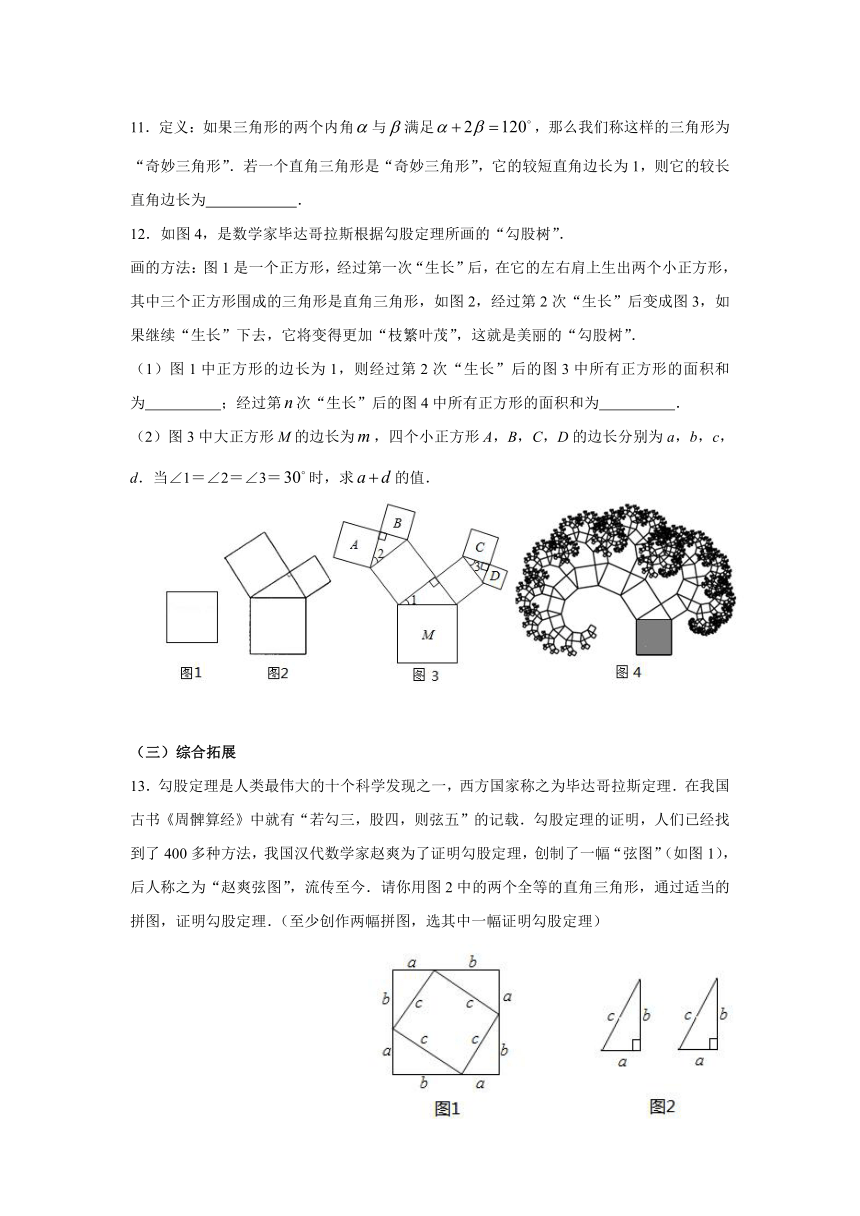
12.如图4,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.
画的方法:图1是一个正方形,经过第一次“生长”后,在它的左右肩上生出两个小正方形,其中三个正方形围成的三角形是直角三角形,如图2,经过第2次“生长”后变成图3,如果继续“生长”下去,它将变得更加“枝繁叶茂”,这就是美丽的“勾股树”.
(1)图1中正方形的边长为1,则经过第2次“生长”后的图3中所有正方形的面积和为 ;经过第次“生长”后的图4中所有正方形的面积和为 .
(2)图3中大正方形M的边长为,四个小正方形A,B,C,D的边长分别为a,b,c,d.当∠1=∠2=∠3=时,求的值.
(三)综合拓展
13.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载.勾股定理的证明,人们已经找到了400多种方法,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.请你用图2中的两个全等的直角三角形,通过适当的拼图,证明勾股定理.(至少创作两幅拼图,选其中一幅证明勾股定理)
14.△ABC中,BC=a,AC=b,AB=c.
情景再现
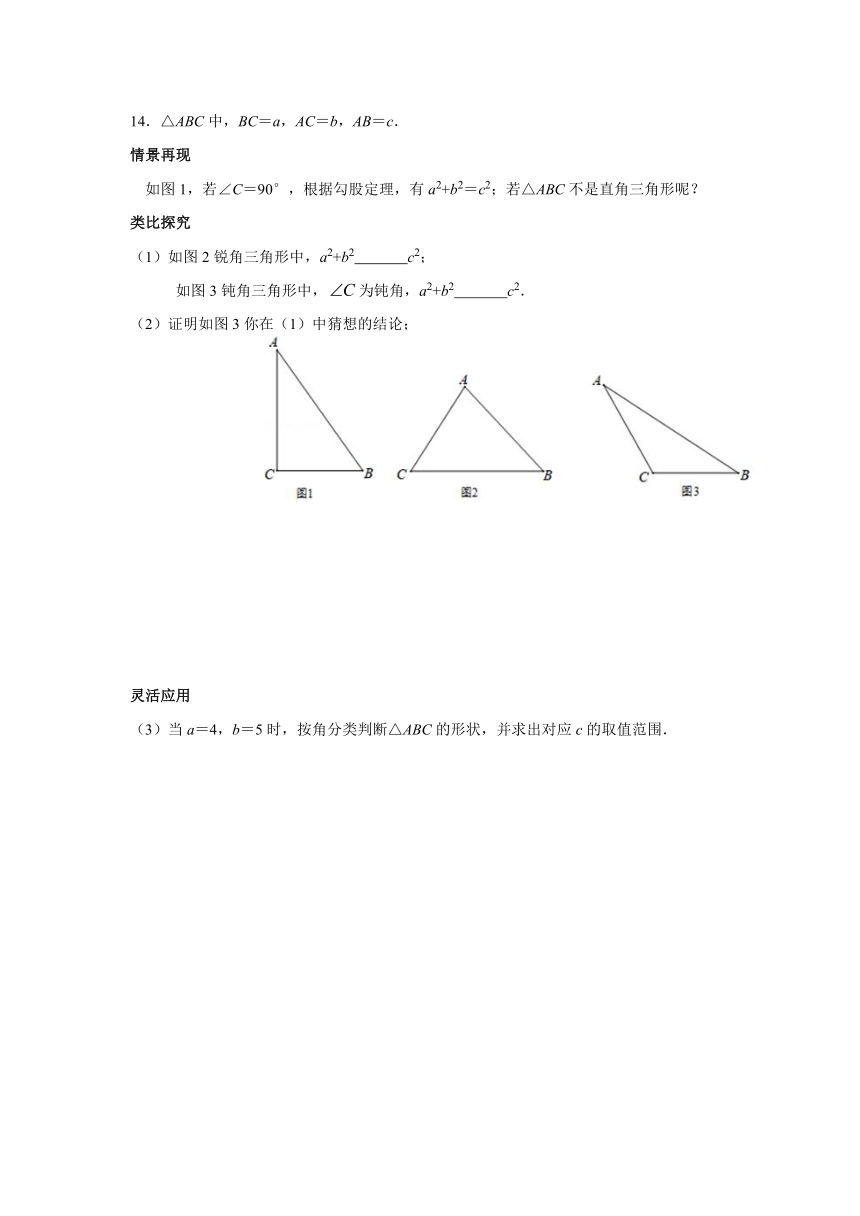
如图1,若∠C=90°,根据勾股定理,有a2+b2=c2;若△ABC不是直角三角形呢?
类比探究
(1)如图2锐角三角形中,a2+b2 c2;
如图3钝角三角形中,为钝角,a2+b2 c2.
(2)证明如图3你在(1)中猜想的结论;
灵活应用
(3)当a=4,b=5时,按角分类判断△ABC的形状,并求出对应c的取值范围.
四、作业答案
1.C 2.B 3.D 4.79 5.5或4 6.
7.关键用HL证明 8.关键证明为等腰三角形,而后用勾股定理计算 9.10. 11.
12.(1)3,. (2)由题意可得,,,,可解得,,..
13.如图,构造两种皆可.
以图3证明为例:
证明:如图5,连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)
∴a2+b2=c2
14.(1)>;<.
(2)如图3,作AC边上的高BD,在直角ADB中BDC中,设CD=x,
则:c2﹣(b+x)2=BD2=a2﹣x2
整理得:a2+b2=c2﹣2bx
∵2bx>0,∴a2+b2<c2.
(3)∵a=4,b=5 ∴
当△ABC为直角三角形时①为斜边
②为直角边
由线段图可知:当△ABC为锐角三角形时
当△ABC为锐角三角形时 或
五、设计意图----特色说明
第9题:设置了轴对称变换的操作,融入了斜边上的中线等于斜边一半这一重要定理,通过等腰三角形、平行线、折叠性质挖掘出特殊角,根据特殊三角形的三边关系解决此题。
第10题:选材于教材中的阅读材料,在直角三角形的条件下,面积的等量关系。出题时一方面将直角三角形条件隐去,以勾股定理逆定理的方式给出,发掘出直角三角形;另一方面向外变成三个正六边形,虽学生对正六边形陌生,但面积关系依旧,根据等式的相关性质,突破所求问题就是哪块面积。
第11题:本题以自定义的方式呈现,考查了直角三角形的两锐角互余的性质,考查了含的直角三角形三边关系,考查了含的直角三角形三边关系的探究法,考查了分类讨论思想、数形结合的数学思想、转化的数学思想等。
第13题:考查学生动手操作的能力,考查学生几何问题的证明能力,考查面积法证明等量关系。通过此种题目,培养学生创造的能力,让学生把勾股定理掌握的更深刻透彻。
第14题:考查了勾股定理,双勾股定理,不等式等内容,考查了分类的数学思想,数形结合的数学思想,培养学生发散的数学思想,考查通过所学内容类比得到新知,是培养学生一种良好的思考习惯,。
六、作业展示
一、作业目标
1.巩固直角三角形的性质及判定,会判断一个三角形是直角三角形,会运用直角三角形的性质解决有关图形的论证、计算等问题。
2.熟练掌握勾股定理并运用勾股定理解决几何问题,会利用勾股定理的逆定理判定一个三角形为直角三角形。
3.巩固判定两个直角三角形全等的方法,用利用角平分线的定理与逆定理解决几何问题。
4.利用类比的方法,让学会学会探究新问题,体验数学的应用价值及学习成就感。
二、使用建议
建议学生学习完浙教版八上2.6,2.7,2.8后使用或八上第二章学习完后使用。
三、作业呈现
(一)立足基础
1.已知△ABC的三边为,具备下列条件的△ABC,不是直角三角形的是( )
A.∠A﹣∠B=∠C B.
C.∠A:∠B:∠C=3:4:5 D.
2.如图,某社会实践学习小组为测量学校A与河对岸江景房B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=30米.由此可求得学校与江景房之间的距离AB等于( )
A.15米 B.60米 C.80米 D.120米
3.如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,添加一个条件,不能使得
Rt△ABC≌Rt△DCB的是( )
A.AB=DC B.AC=DB C.∠ABC=∠DCB D.BC=BD
(第2题) (第3题)
4.如图,在ABC中,∠C=90°,AC=4cm,BC=9cm.以AB为一边在ABC的同侧作正方形ABDE,则图中阴影部分的面积为 .
5.直角三角形的两条边分别为6、8,则斜边上的中线长为.
6.如图,Rt△ABC中,∠ACB=90°,∠ABC=70°,∠ACB的平分线与外角∠ABD的平分线交于点E,连接AE,则∠BAE的度数为 .
(第4题) (第6题)
7.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,
BE=CF.求证:OA=OD.
8.如图,Rt△ABC中,∠CAB=90°,ABD是等腰三角形,AB=BD=4,CBBD,
交AD于E,BE=1,求AC的长.
(二)能力提升
9.如图,在ABC中,∠ACB=,AC=6,CD是斜边AB上的中线,以CD为折痕将
ACD折叠得到ECD,如果,则的值为 .
10.如图,在ABC中,,,,以各边为边在AB的同侧作三个正六边形,形成三块阴影面积分别为,则的值为 .
(第9题) (第10题)
11.定义:如果三角形的两个内角与满足,那么我们称这样的三角形为“奇妙三角形”.若一个直角三角形是“奇妙三角形”,它的较短直角边长为1,则它的较长直角边长为 .
12.如图4,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.
画的方法:图1是一个正方形,经过第一次“生长”后,在它的左右肩上生出两个小正方形,其中三个正方形围成的三角形是直角三角形,如图2,经过第2次“生长”后变成图3,如果继续“生长”下去,它将变得更加“枝繁叶茂”,这就是美丽的“勾股树”.
(1)图1中正方形的边长为1,则经过第2次“生长”后的图3中所有正方形的面积和为 ;经过第次“生长”后的图4中所有正方形的面积和为 .
(2)图3中大正方形M的边长为,四个小正方形A,B,C,D的边长分别为a,b,c,d.当∠1=∠2=∠3=时,求的值.
(三)综合拓展
13.勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载.勾股定理的证明,人们已经找到了400多种方法,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.请你用图2中的两个全等的直角三角形,通过适当的拼图,证明勾股定理.(至少创作两幅拼图,选其中一幅证明勾股定理)
14.△ABC中,BC=a,AC=b,AB=c.
情景再现
如图1,若∠C=90°,根据勾股定理,有a2+b2=c2;若△ABC不是直角三角形呢?
类比探究
(1)如图2锐角三角形中,a2+b2 c2;
如图3钝角三角形中,为钝角,a2+b2 c2.
(2)证明如图3你在(1)中猜想的结论;
灵活应用
(3)当a=4,b=5时,按角分类判断△ABC的形状,并求出对应c的取值范围.
四、作业答案
1.C 2.B 3.D 4.79 5.5或4 6.
7.关键用HL证明 8.关键证明为等腰三角形,而后用勾股定理计算 9.10. 11.
12.(1)3,. (2)由题意可得,,,,可解得,,..
13.如图,构造两种皆可.
以图3证明为例:
证明:如图5,连接DB,过点D作BC边上的高DF,则DF=EC=b﹣a
∵S四边形ADCB=S△ACD+S△ABC=b2+ab.
又∵S四边形ADCB=S△ADB+S△DCB=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)
∴a2+b2=c2
14.(1)>;<.
(2)如图3,作AC边上的高BD,在直角ADB中BDC中,设CD=x,
则:c2﹣(b+x)2=BD2=a2﹣x2
整理得:a2+b2=c2﹣2bx
∵2bx>0,∴a2+b2<c2.
(3)∵a=4,b=5 ∴
当△ABC为直角三角形时①为斜边
②为直角边
由线段图可知:当△ABC为锐角三角形时
当△ABC为锐角三角形时 或
五、设计意图----特色说明
第9题:设置了轴对称变换的操作,融入了斜边上的中线等于斜边一半这一重要定理,通过等腰三角形、平行线、折叠性质挖掘出特殊角,根据特殊三角形的三边关系解决此题。
第10题:选材于教材中的阅读材料,在直角三角形的条件下,面积的等量关系。出题时一方面将直角三角形条件隐去,以勾股定理逆定理的方式给出,发掘出直角三角形;另一方面向外变成三个正六边形,虽学生对正六边形陌生,但面积关系依旧,根据等式的相关性质,突破所求问题就是哪块面积。
第11题:本题以自定义的方式呈现,考查了直角三角形的两锐角互余的性质,考查了含的直角三角形三边关系,考查了含的直角三角形三边关系的探究法,考查了分类讨论思想、数形结合的数学思想、转化的数学思想等。
第13题:考查学生动手操作的能力,考查学生几何问题的证明能力,考查面积法证明等量关系。通过此种题目,培养学生创造的能力,让学生把勾股定理掌握的更深刻透彻。
第14题:考查了勾股定理,双勾股定理,不等式等内容,考查了分类的数学思想,数形结合的数学思想,培养学生发散的数学思想,考查通过所学内容类比得到新知,是培养学生一种良好的思考习惯,。
六、作业展示
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
