第3章 数据分析初步 练习题 (含解析)2021-2022学年浙江省各地浙教版数学八年级下册期末试题选编
文档属性
| 名称 | 第3章 数据分析初步 练习题 (含解析)2021-2022学年浙江省各地浙教版数学八年级下册期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-02 20:54:37 | ||
图片预览



文档简介
第3章 数据分析初步
一、单选题
1.(2022春·浙江金华·八年级统考期末)某班40名同学一周参加体育锻炼时间统计如表所示:
时间/h 6 7 8 9
人数 2 18 14 6
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.18,7.5 B.18,7 C.7,8 D.7,7.5
2.(2022春·浙江杭州·八年级统考期末)某小组4名同学的英语口试成绩依次为27,23,25,29,这组数据的中位数是( )
A.24 B.25 C.26 D.27
3.(2022春·浙江金华·八年级统考期末)在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数 B.方差 C.平均数 D.中位数
4.(2022春·浙江宁波·八年级统考期末)有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
5.(2022春·浙江金华·八年级统考期末)“科学用眼,保护视力”是青少年珍爱生命的具体表现,某班50名同学的视力检查数据如下表:
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 2 3 6 9 12 10 5 3
则视力的众数是( )
A.4.5 B.4.6 C.4.7 D.4.8
6.(2022春·浙江衢州·八年级统考期末)一家鞋店对上周某一品牌的销售情况统计如下表:
尺码(厘米) 22.5 23 23.5 24 24.5
销售量(双) 2 5 11 7 3
该店决定本周进鞋时多进些尺码为23.5厘米的鞋,影响鞋店决策的统计量是( ).
A.平均数 B.中位数 C.众数 D.方差
7.(2022春·浙江宁波·八年级统考期末)在一次素养比赛中,6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
8.(2022春·浙江舟山·八年级统考期末)若一组数据平均数为17,方差为2,则另一组数据的平均数和方差分别为( )
A.18,2 B.17,2 C.17,3 D.18,3
9.(2022春·浙江湖州·八年级统考期末)下表记录了甲、乙、丙、丁四名射箭选手10次测试成绩的平均数与方差:
甲 乙 丙 丁
平均数(分) 9.5 9.5 9.2 9.2
方差 3.6 7.4 3.6 7.4
要选择一名成绩好且发挥稳定的选手参加射箭比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
10.(2022春·浙江金华·八年级统考期末)测试五位学生的“一分钟仰卧起坐”成绩,得到五个各不相同的数据. 在统计时,出现了一处错误:将最高成绩50个写成了55个.则下列统计量不受影响的是( )
A.方差 B.标准差 C.中位数 D.平均数
二、解答题
11.(2022春·浙江湖州·八年级统考期末)某单位450名职工积极参加想贫困地区捐书活动,为了解职工的捐书两,采用随机抽样的方法抽取了30名职工作为样本,对他们的涓蜀梁进行统计,统计结果共有4本,5本,6本,7本,8本,五类,分别用A,B,C,D,E表示,根据统计数据绘制成了如图所示不完整的条形统计图,用图中所给的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本书的平均数;
(3)估计该单位450名职工共捐书多少本?
12.(2022春·浙江金华·八年级统考期末)学校准备从甲乙两位选手中选择一位,代表学校参加所在地区的汉字听写大赛,总评成绩由“表达能力、阅读理解、综合素质和汉字听写”四部分组成.甲,乙两位选手的成绩如下表,请解答下列问题:
选手 表达能力 阅读理解 综合素质 汉字听写
甲 85 78 85 73
乙 73 80 82 83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩.
(2)已知四部分占总评成绩的比例如图所示.
①求图中表示“阅读理解”的扇形的圆心角度数;
②通过计算甲,乙两名选手的总评成绩,你认为学校派谁参加比赛合适?
13.(2022春·浙江衢州·八年级统考期末)北京冬奥会女子大跳台决赛的打分规则;6名裁判打分,去除一个最高分和一个最低分,剩余4个分数的平均值为该选手成绩.下表是中国选手谷爱凌第一跳的得分情况,其中裁判4,裁判5的打分(分别为94分和a分)被去除.
裁判1 裁判2 裁判3 裁判4 裁判5 裁判6 成绩
94分 94分 94分 b分 93.75分
请根据表中信息,解决以下问题;
(1)求b的值.
(2)判断a是否最低分并说明理由.
(3)从平均数的特征说说打分规则中去除一个最高分及一个最低分的合理性.
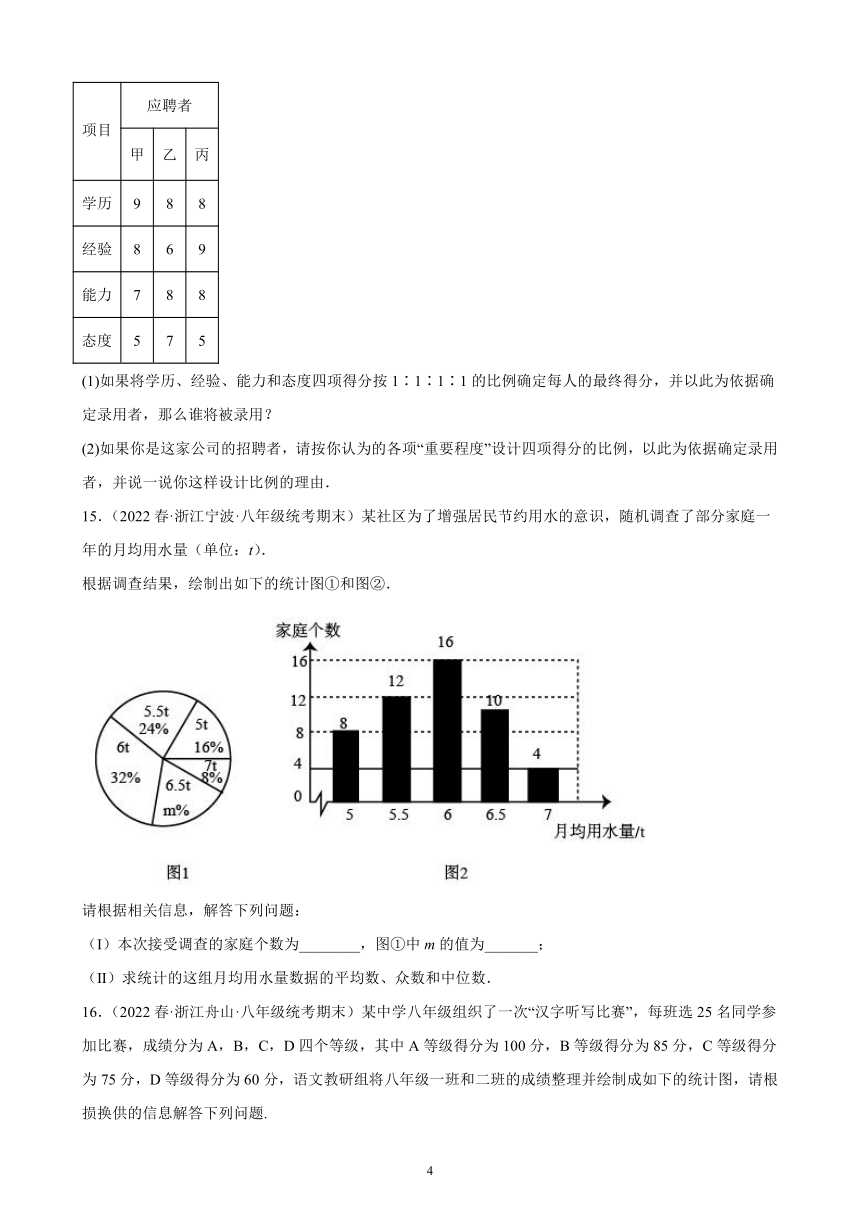
14.(2022春·浙江杭州·八年级统考期末)某公司要招聘一名职员,根据实际需要,从学历、经验、能力和态度四个方面对甲、乙、丙三名应聘者进行了测试,测试成绩如下表.
项目 应聘者
甲 乙 丙
学历 9 8 8
经验 8 6 9
能力 7 8 8
态度 5 7 5
(1)如果将学历、经验、能力和态度四项得分按1∶1∶1∶1的比例确定每人的最终得分,并以此为依据确定录用者,那么谁将被录用?
(2)如果你是这家公司的招聘者,请按你认为的各项“重要程度”设计四项得分的比例,以此为依据确定录用者,并说一说你这样设计比例的理由.
15.(2022春·浙江宁波·八年级统考期末)某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).
根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为________,图①中m的值为_______;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
16.(2022春·浙江舟山·八年级统考期末)某中学八年级组织了一次“汉字听写比赛”,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,语文教研组将八年级一班和二班的成绩整理并绘制成如下的统计图,请根损换供的信息解答下列问题.
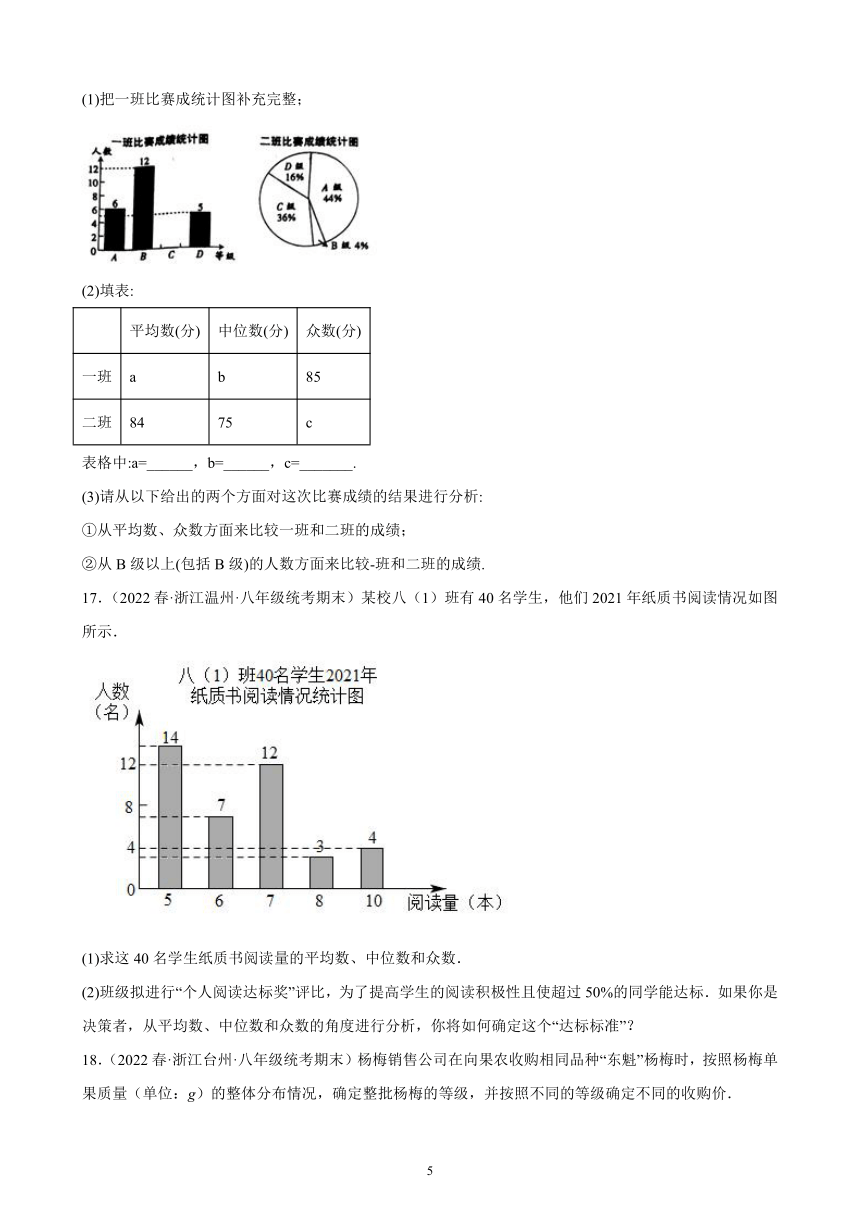
(1)把一班比赛成统计图补充完整;
(2)填表:
平均数(分) 中位数(分) 众数(分)
一班 a b 85
二班 84 75 c
表格中:a=______,b=______,c=_______.
(3)请从以下给出的两个方面对这次比赛成绩的结果进行分析:
①从平均数、众数方面来比较一班和二班的成绩;
②从B级以上(包括B级)的人数方面来比较-班和二班的成绩.
17.(2022春·浙江温州·八年级统考期末)某校八(1)班有40名学生,他们2021年纸质书阅读情况如图所示.
(1)求这40名学生纸质书阅读量的平均数、中位数和众数.
(2)班级拟进行“个人阅读达标奖”评比,为了提高学生的阅读积极性且使超过50%的同学能达标.如果你是决策者,从平均数、中位数和众数的角度进行分析,你将如何确定这个“达标标准”?
18.(2022春·浙江台州·八年级统考期末)杨梅销售公司在向果农收购相同品种“东魁”杨梅时,按照杨梅单果质量(单位:g)的整体分布情况,确定整批杨梅的等级,并按照不同的等级确定不同的收购价.
果农老张和老王各送来一批杨梅,收购员小李在他们送来的杨梅中分别随机抽检了100颗,秤出质量(单位:g),并把收集到的数据整理成下表:
杨梅单果质量(g) 二等() 一等() 优等() 特优()
组中值 17.5 22.5 27.5 32.5
老张家杨梅数量(个) 20 32 26 22
老王家杨梅数量(个) 14 26 36 24
(1)若用扇形图描述老王家各个等级杨梅的比例,其表示特优杨梅的扇形的圆心角是_______°.
(2)从杨梅单果质量的平均数看,你认为老张家杨梅的收购价与老王家杨梅的收购价应该相同吗?请说明理由.
(3)结果,收购员小李给老张家杨梅定的收购价比老王家的杨梅收购价低一个等级,你能用统计知识解释小李这样做的合理性吗?
19.(2022春·浙江宁波·八年级统考期末)毛泽东同志曾说“德志皆寄予于体,无体是无德志也”,某社区为了加强社区居民对冬奥会的了解,鼓励社区居民在线参与作答《2022年北京冬奥会知识点》模拟试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩(单位:分)进行统计、分析,过程如下:
【收集数据】
甲:85,80,95,100,90,95,85,65,75,85,89,90,70,90,100,80,80,90,96,75;
乙:80,60,80,95,65,100,90,85,85,80,95,75,80.90,70,80,95,75,100,90.
【整理数据】
成绩x 60≤x≤70 70<x≤80 80<x≤90 90<x≤100
甲小区 2 5 a b
乙小区 3 7 5 5
【分析数据】
统计量 平均数 中位数 众数
甲小区 85.75 87.5 c
乙小区 83.5 d 80
【应用数据】
(1)填空:a= ,b= ,c= ,d= ;
(2)若甲小区共有600人参与答卷,请估计甲小区成绩大于80分的人数;
(3)你认为甲、乙两个小区哪一个对冬奥会知识掌握更好?请写出一条理由.
20.(2022春·浙江杭州·八年级统考期末)某次数学测试,圆圆同学所在的学习小组其他同学的平均分为75分,圆圆说,“我的分是100分,我们学习小组的平均分恰好是80分”.
(1)圆圆同学所在的学习小组具有多少人?
(2)已知该学习小组本次测试得分的众数是90分,最低分为50分,求该学习小组本次测试得分的中位数.
21.(2022春·浙江金华·八年级统考期末)按照疫情防控工作部署,学校核酸检测有序进行,已知检测员甲和检测员乙到某校进行核酸检测,分别记录两人检测前6名学生所用的时间,获得如下检测时间折线统计图,根据图中信息,解答下列问题:
(1)要评价每位检测员检测时间平均水平,你选择什么统计量?求这个统计量.
(2)求检测员乙检测时间的方差.
(3)现求得检测员甲检测时间的方差(单位:平方秒)根据折线统计图及上面两个小题的计算,你认为哪位检测员的检测技术比较娴熟?请简述理由.
22.(2022春·浙江绍兴·八年级统考期末)2022年冬奥会在北京举行,为了增进学生对冰雪文化的了解,我校开展了冰雪运动相关知识的宣传教育活动,提高了学生对冰雪运动的关注度,并掀起了模拟冰雪运动的热潮.在模拟冰壶比赛中,规定得6分及以上为合格,得8分及以上为优秀.学校从参加比赛的七、八年级学生中各随机抽取了15名学生的比赛成绩,他们的成绩如下表:
成绩(分) 4 5 6 7 8 9
七年级(人) 1 2 5 2 1 4
八年级(人) 1 1 4 5 2 2
模拟冰壶比赛得分统计如下:
统计量平均分中位数众数方差合格率
统计量 平均分 中位数 众数 方差 合格率
七年级 6.8 m 6 2.56 80.0%
八年级 6.8 7 n 1.76 86.7%
(1)m=_______;n=_________;
(2)你认为哪个年级的模拟冰壶比赛成绩更优秀?请说明理由;
(3)若七、八年级参加模拟冰壶比赛的人数分别600人和450人,求这两个年级共有多少学生的模拟冰壶比赛成绩为优秀等级?
三、填空题
23.(2022春·浙江温州·八年级统考期末)已知一组数据2,1,,6的平均数是4,则的值为_______.
24.(2022春·浙江金华·八年级统考期末)某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为95分、85分、90分,综合成绩按笔试、试讲、面试的占比为2:2:1,则该名教师的综合成绩为_____.
25.(2022春·浙江宁波·八年级统考期末)2021年6月17日,中国第7艘载人航天飞船“神舟12号”圆满发射成功,激励更多的年轻人投身航天事业.现对学员们进行招飞前考核,其中某位学员心理素质、身体素质、科学头脑、应变能力四项测试得分分别为86分、85分、88分、90分,若按照心理素质、身体素质、科学头脑、应变能力的占比为4∶3∶2∶1的比例确定总分,则该名学员的总分为______________分.
26.(2022春·浙江湖州·八年级统考期末)若一组数据1,5,2,3,x,y的平均数为3,众数也为3,则这组数据的中位数为_________.
27.(2022春·浙江湖州·八年级统考期末)某人5次射击命中的环数分别为5,10,7,x,10,若这组数据的中位数为8,则这组数据的方差为________.
28.(2022春·浙江台州·八年级统考期末)甲、乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差s2甲与s2乙的大小关系是s2甲_______s2乙.(填“>”或“<”)
29.(2022春·浙江金华·八年级统考期末)某天的最低气温是﹣2℃,最高气温是10℃,则这天气温的极差为_____℃.
参考答案:
1.D
【分析】根据众数和中位数的定义进行求解即可得出答案.
【详解】解:根据题意可得,参加体育锻炼时间的众数为7,
因为该班有40名同学,所以中位数为第20和21名同学时间,第20名同学的时间为,第21名同学的时间为,
所以中位数为.
故选:D.
【点睛】考查了中位数、众数的概念.本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
2.C
【分析】将这组数据从小到大重新排列,再根据中位数的定义求解即可.
【详解】将这组数据从小到大重新排列为23,25,27,29,
∴这组数据的中位数为,
故选:C.
【点睛】本题主要考查中位数,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
3.D
【分析】根据中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)的意义,9人成绩的中位数是第5名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.
故选:D.
【点睛】本题考查了统计量的选择,熟练掌握众数,方差,平均数,中位数的概念是解题的关键.
4.B
【分析】根据中位数的定义求解即可.
【详解】去掉一个最高分和一个最低分对中位数没有影响.
故选:B.
【点睛】本题考查了统计量的选择,解题的关键是了解中位数的定义.
5.C
【分析】出现次数最多的数据是样本的众数,根据定义解答.
【详解】解:∵4.7出现的次数最多,∴视力的众数是4.7,
故选:C.
【点睛】此题考查了众数的定义,熟记定义是解题的关键.
6.C
【分析】根据各个选项的意义进行判断即可得到答案.
【详解】观察各个尺码的鞋的销售量知,尺码为23.5厘米的鞋销售量最多,
即影响鞋店决策的统计量是众数.
故选:C.
【点睛】本题考查统计的相关知识,掌握平均数、中位数、众数、方差的意义是关键.
7.B
【分析】利用已知条件可知统计时误将一位学生的成绩65分记成了60分,平均数和方差都要变,可对A,D作出判断;同时众数也要变化,可对C作出判断;此时的中位数不变,可对B作出判断.
【详解】解:∵6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,
∴众数要变,故C不符合题意;平均数与每个数有关,因此平均数也要变,故A不符合题意;方差与每个数据有关,数据变了方差也要变化,故D不符合题意;中位数是82.5,不会变化,故B符合题意;
故答案为:B.
【点睛】本题考查了平均数;中位数;方差;众数等知识,掌握平均数、方差、中位数、众数的含义是解题的关键.
8.A
【分析】根据平均数和方差的变化规律,即可得出答案.
【详解】解:由题意得,数据的平均数为,
=
=
=
=18,
∵方差为2,
∴的方差不变,也是2,
故选:A.
【点睛】本题考查了方差与平均数,用到的知识点:如果一组数据的平均数为,方差为,那么另一组数据的平均数为,方差为,熟练掌握相关知识点是解题关键 .
9.A
【分析】根据平均数反映了成绩的好差,方差反映数据的稳定性.选择成绩好且发挥稳定,选择平均数大,方差小的选手,即可.
【详解】∵平均数:,方差:,选择平均数大,方差小的值
∴选择甲.
故选:A.
【点睛】本题考查平均数、方差,灵活掌握平均数,方差在数据中运用是解题的关键.
10.C
【分析】根据中位数的定义解答可得.
【详解】解:因为中位数是将数据按照大小顺序重新排列,代表了这组数据值大小的“中点”,不受极端值影响,
所以将最高成绩写得更高了,50个写成了55个,计算结果不受影响的是中位数,
故选:C.
【点睛】本题主要考查方差、极差、中位数和平均数,解题的关键是掌握中位数的定义.
11.(1)见解析
(2)这30名职工捐书本数的平均数为6本
(3)估计该单位450名职工共捐书2700本
【分析】(1)根据题目中的数据和条形统计图中的数据,可以计算出捐D类书的人数,从而可以将条形统计图补充完整;
(2)根据条形统计图中的数据,可以计算出平均数;
(3)根据(2)中的平均数,可以计算出该单位450名职工共捐书多少本.
【详解】(1)捐D类书的有30﹣4﹣6﹣9﹣3=8(人),
补全的条形统计图如下图所示:
(2)(4×4+5×6+6×9+7×8+8×3)=6(本),
答:这30名职工捐书本数的平均数为6本.
(3)450×6=2700(本),
答:估计该单位450名职工共捐书2700本.
【点睛】本题主要条形统计图画法、求平均数、用样本估计总体等知识,理解掌握相关概念与计算公式是解题关键.
12.(1)79.5
(2)①;②学校派乙参加比赛合适
【分析】(1)根据平均数的定义求解即可;
(2)①用360度乘以阅读理解的占比即可得到答案;②分别求出甲、乙两人的总成绩即可得到答案.
(1)
解:由题意得,乙的平均成绩为;
(2)
解:①由题意得:
图中表示“阅读理解”的扇形的圆心角度数为
②甲的总成绩为:,
乙的总成绩为:,
∵80.4>79.5,
∴学校派乙参加比赛合适.
【点睛】本题主要考查了求平均数,求加权平均数,求扇形圆心角度数,利用平均数做决策等等,正确理解题意是解题的关键.
13.(1)93
(2)a是最低分,只有当a≤93符合题意,否则就不满足平均数是93.75,且去掉的是94分和a分;
(3)由于平均数容易受到极端值的影响而发生变化,因此去除一个最高分及一个最低分可以避免平均数受极端值的影响.
【分析】(1)根据平均数的计算方法进行计算即可;
(2)根据计算成绩的方法进行判断即可;
(3)根据影响平均数的因素进行判断即可.
【详解】(1)解:由题意得,
解得b=93,
答:b的值为93;
(2)解:a是最低分,由题意可知a≤93,否则就不满足平均数是93.75,且去掉的是94分和a分;
(3)解:由于平均数容易受到极端值的影响而发生变化,因此去除一个最高分及一个最低分可以避免平均数受极端值的影响.
【点睛】本题考查算术平均数,理解平均数的意义,掌握平均数的计算方法是解决问题的前提.
14.(1)丙将被录用
(2)见解析
【分析】(1)计算算术平均数即可;
(2)计算加权平均数即可.
【详解】(1)解:依题意,
甲的平均分为,
乙的平均分为,
丙的平均分为,
则丙的平均分最高,因此丙被录用.
(2)解:如果将学历、经验、能力和态度四项得分按3:2:3:2的比例确定每人的最终得分,
则甲的得分为,
乙的得分为,
比丙的得分为,
丙的得分最高,因此丙被录用.
理由:因为数据中的“权”反映数据的相对“重要程度”,权越大,该数据占的比重越大,反之则越小.
【点睛】本题考查了算术平均数、加权平均数,熟练掌握加权平均数的意义和计算公式是解答的关键.
15.(Ⅰ)50,20;(Ⅱ)这组数据的平均数是5.9;众数为6;中位数为6.
【分析】(Ⅰ)利用用水量为5t的家庭个数除以其所占百分比即可求出本次接受调查的家庭个数;利用用水量为6.5t的家庭个数除以本次接受调查的家庭个数即得出其所占百分比,即得出m的值.
(Ⅱ)根据加权平均数的公式,中位数,众数的定义即可求出结果.
【详解】(Ⅰ)本次接受调查的家庭个数=,
由题意可知 ,
解得.
故答案为50,20.
(Ⅱ)观察条形统计图,
∵,
∴这组数据的平均数是5.9.
∵在这组数据中,6出现了16次,出现的次数最多,
∴这组数据的众数为6.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是6,
即有,
∴这组数据的中位数为6.
【点睛】本题考查条形统计图与扇形统计图相关联,加权平均数,中位数以及众数.从条形统计图与扇形统计图中找到必要的数据和信息是解答本题的关键.
16.(1) 统计图补充完整如图所示见解析;(2)二班的平均数为:a=82.8 ,一班的中位数为:b=85, 二班的众数为:c=100 ; (3)①从平均数和众数的角度来比较二班的成绩更好;②从B级以上(包括B级)的人数的角度来比较一班的成绩更好.
【分析】(1)根据题意和表格中的数据可以求得一班C等级的学生数,从而可以解答本题;
(2)根据表格中的数据可以求得一班的平均数和中位数,以及二班的众数;
(3)根据表格中的数据,可以从两方面比较一班和二班成绩的情况.
【详解】解:(1)一班中C级的有25-6-12-5=2人
如图所示
(2) 一班的平均数为:a= =82.8,
一班的中位数为:b=85
二班的众数为:c=100 ;
(3)①从平均数和众数的角度来比较二班的成绩更好;
②从B级以上(包括B级)的人数的角度来比较一班的成绩更好.
故答案为(1) 统计图补充完整如图所示见解析;(2)二班的平均数为:a=82.8 ,一班的中位数为:b=85, 二班的众数为:c=100 ; (3)①从平均数和众数的角度来比较二班的成绩更好;②从B级以上(包括B级)的人数的角度来比较一班的成绩更好.
【点睛】本题考查条形统计图、扇形统计图、众数、中位数、加权平均数,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
17.(1)平均数是6.5、中位数是6、众数是5
(2)选择中位数作为标准,理由见解析
【分析】(1)根据40名学生纸质书阅读量总数除以总人数,求得平均数;中位数就是大小处于中间位置的数,众数就是出现次数最多的数,根据定义判断即可;
(2)根据求出的这40名学生阅读量的平均数、中位数和众数的角度,各个角度分析即可.
(1)
解:平均数:,
中位数,
众数是5;
(2)
当标准为平均数6.5本,达到标准的学生有19人未超过50%;
当标准为中位数6本,达到标准的学生有26人超过50%,有利于提高学生的积极性;
当标准为众数5本,40名学生都达到标准,但不利于提高学生的积极性;
因此应该选择中位数作为标准.
【点睛】本题考查的是统计的应用,读懂统计表,从统计表中得到必要的信息是解决问题的关键.本题也考查了平均数、中位数、众数的认识.
18.(1)86.4
(2)应该相同,理由见解析
(3)见解析,理由见解析
【分析】(1)用360°乘以老王家特优杨梅的频率即可;
(2)分别求出两家的平均数,即可比较出来;
(3)根据所求数据进行分析即可.
【详解】(1)解:360°×=86.4°,
故答案为:86.4;
(2)解:老张家杨梅的等级的平均数为(克)
老王家:(克)
从平均数看,根据样本估计总体,老张家与老王家的杨梅单颗质量平均数落在同一级别中,所以两家收购价应该相同;
(3)解:从中位数角度来看,根据样本估计总体,老张家的杨梅单颗质量中位数落在组,属于一等品;而老王家的杨梅单颗质量中位数落在组,属于优等品,因此收购员小李给老张家杨梅定的收购价比老王家的杨梅收购价低一个等级也是合理的.
【点睛】本题考查扇形统计图,平均数及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
19.(1)8;5;90;82.5;
(2)390人;
(3)甲小区,理由见解析.
【分析】(1)直接根据收集的数据以及众数、中位数的定义求解即可;
(2)用600乘以甲小区成绩大于80分的人数所占比例即可;
(3)直接比较两小区的平均数、中位数、众数即可.
(1)
由甲小区抽取的20名人员的答卷成绩可知a=8,b=5,
甲的数据:85,80,95,100,90,95,85,65,75,85,89,90,70,90,100,80,80,90,96,75;
从中可以得出数据90出现的次数最多,得出c=90,
把乙小区抽取的20名人员的答卷成绩排序为:60,65,70,75,75,80,80,80,80,80,85,85,90,90,90,95,95,95,100,100,
则乙小区成绩的中位数为=82.5(分),
故答案为:8,5,90,82.5;
(2)
估计甲小区成绩大于80分的人数为600×=390(人)
(3)
甲小区对冬奥会知识掌握更好,
理由:甲小区的平均数、中位数、众数均大于乙小区的.
【点睛】本题主要考查统计图表及数据的收集宇整理知识,熟练掌握众数、平均数、中位数的定义、用样本估计总体的方法是解题的关键.
20.(1)圆圆同学所在的学习小组有5人;
(2)该学习小组本次测试得分的中位数是90分.
【分析】(1)利用平均数的定义直接计算即可;
(2)利用众数,中位数的定义即可求解.
【详解】(1)解:根据题意得:(100- 75) ÷ (80- 75)= 5(人),
∴圆圆同学所在的学习小组有5人;
(2)解:该学习小组有5人,最低分为50分,圆圆的分是100分,
∵众数是90分,
∴本次测试得分是90分的有2人,最低分为50分,
∴该学习小组本次测试还有一个得分是80×5-(50+ 90×2+100)= 70(分),
∴该学习小组本次测试得分从小到大排列为50,70,90, 90,100,
∴该学习小组本次测试得分的中位数是90分.
【点睛】本题考查的是平均数,众数,中位数,弄清题意是解本题的关键.
21.(1)平均值,,
(2)
(3)检测员乙的检测技术较娴熟,见解析
【分析】(1)根据题意,要评价每位检测员检测时间平均水平,选择平均数,根据折线统计图求得甲、乙的数据,进而求得平均数即可求解;
(2)根据方差公式进行计算即可求解;
(3)比较甲乙的方差大小即可求解.
【详解】(1)解:∵要评价每位检测员检测时间平均水平,
∴选择平均数,
根据统计图可知,甲:7,6,6,9,10,10,
平均数为,
乙:7,8,7,10,7,9,
,
(2);
(3)检测员乙的检测技术较娴熟,理由如下,
,,,,
,
检测员乙的检测技术较娴熟.
【点睛】本题考查了折线统计图,选择合适的统计量,求平均数,求方差,掌握以上知识是解题的关键.
22.(1)6;7
(2)八年级的模拟冰壶比赛成绩更优秀,理由见解析
(3)320
【分析】(1)根据一组数据按从小到大或从大到小的顺序排列后中间的数叫做中位数,出现次数最多的数叫做众数,即可求解;
(2)从平均成绩、众数、方差、合格率几方面分析,即可求解;
(3)分别求出七年级和八年级的比赛成绩为优秀等级人数,即可求解.
(1)
解:∵七年级15人的成绩的第8个数为6分,
∴七年级15人的成绩的中位数为6分,即m =6;
∵八年级15人的成绩中最多的是7分,
∴众数为7分,即n=7,
故答案为:6;7;
(2)
八年级的模拟冰壶比赛成绩更优秀,理由如下:
从平均成绩看,两个年级的成绩一样,从中位数看,八年级的成绩好些,从众数看,八年级成绩更好,从方差看,八年级成绩的方差小于七年级成绩的方差,方差越小,成绩越稳定,故八年级成绩比七年级成绩稳定,从合格率看比年级成绩的合格率比七年级成绩的合格率高,综合以上几点,我认为八年级的模拟冰壶比赛成绩更优秀;
(3)
解: .
【点睛】本题主要考查了求中位数和众数,利用方差、平均数、中位数做决策,利用样本求总体数量等知识,熟练掌握相关知识点是解题的关键.
23.7
【分析】利用平均数的定义,列出方程即可求解.
【详解】∵一组数据2,1,,6的平均数是4,
∴,
解得,
故答案为:7.
【点睛】本题主要考查了平均数的概念、解一元一次方程.平均数是指在一组数据中所有数据之和再除以数据的个数,熟练掌握知识点是解题的关键.
24.90分
【分析】计算出该教师的加权平均数即可.
【详解】由题意知,该名教师的综合成绩为:(分),
故答案为:90分
【点睛】本题考查了加权平均数,掌握加权平均数的计算公式是关键.
25.86.5
【分析】根据加权平均数的公式进行计算即可求解,加权平均数计算公式为:,其中代表各数据的权.
【详解】解:∵得分分别为86分、85分、88分、90分,按占比为4∶3∶2∶1的比例确定总分,
∴该名学员的总分为
故答案为:86.5
【点睛】本题考查了求加权平均数,掌握加权平均数的计算公式是解题的关键.
26.3
【分析】根据这组数据的众数为3,可确定x和y中至少有一个值为3,再根据平均数为3即可确定另一个值,从而根据中位数的定义求出结果.
【详解】∵这组数据的众数为3,
∴x和y中至少有一个值为3.
∵平均数为3,假设x=3,
∴,
解得:,
∴这组数据按从大到小排列为1,2,3,3,4,5,且符合题意,
∴这组数据的中位数为.
故答案为:3.
【点睛】本题考查平均数、众数和中位数的定义.由平均数和众数具体的求出这组数据是解题关键.
27.3.6
【分析】根据中位数的性质,得;再根据方差的性质计算,即可得到答案.
【详解】根据题意,
∴5次射击命中的环数分别为5,10,7,8,10
∴这组数据的平均数为:
∴这组数据的方差为:
故答案为:3.6.
【点睛】本题考查了数据分析的知识;解题的关键是熟练掌握中位数、方差的性质,从而完成求解.
28.>
【分析】利用方差反映一组数据的波动大小的一个量进行判断.
【详解】解:∵甲地日平均气温的比乙地的日平均气温的变化幅度大,
∴方差s2甲>s2乙.
故答案为>.
【点睛】本题考查了方差:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
29.12
【详解】极差是指一组数据中最大数据与最小数据的差,因此,极差=10℃﹣2℃=12℃.
故答案为:12.
一、单选题
1.(2022春·浙江金华·八年级统考期末)某班40名同学一周参加体育锻炼时间统计如表所示:
时间/h 6 7 8 9
人数 2 18 14 6
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.18,7.5 B.18,7 C.7,8 D.7,7.5
2.(2022春·浙江杭州·八年级统考期末)某小组4名同学的英语口试成绩依次为27,23,25,29,这组数据的中位数是( )
A.24 B.25 C.26 D.27
3.(2022春·浙江金华·八年级统考期末)在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )
A.众数 B.方差 C.平均数 D.中位数
4.(2022春·浙江宁波·八年级统考期末)有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )
A.平均数 B.中位数 C.众数 D.方差
5.(2022春·浙江金华·八年级统考期末)“科学用眼,保护视力”是青少年珍爱生命的具体表现,某班50名同学的视力检查数据如下表:
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 2 3 6 9 12 10 5 3
则视力的众数是( )
A.4.5 B.4.6 C.4.7 D.4.8
6.(2022春·浙江衢州·八年级统考期末)一家鞋店对上周某一品牌的销售情况统计如下表:
尺码(厘米) 22.5 23 23.5 24 24.5
销售量(双) 2 5 11 7 3
该店决定本周进鞋时多进些尺码为23.5厘米的鞋,影响鞋店决策的统计量是( ).
A.平均数 B.中位数 C.众数 D.方差
7.(2022春·浙江宁波·八年级统考期末)在一次素养比赛中,6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,则其中不受影响的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
8.(2022春·浙江舟山·八年级统考期末)若一组数据平均数为17,方差为2,则另一组数据的平均数和方差分别为( )
A.18,2 B.17,2 C.17,3 D.18,3
9.(2022春·浙江湖州·八年级统考期末)下表记录了甲、乙、丙、丁四名射箭选手10次测试成绩的平均数与方差:
甲 乙 丙 丁
平均数(分) 9.5 9.5 9.2 9.2
方差 3.6 7.4 3.6 7.4
要选择一名成绩好且发挥稳定的选手参加射箭比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
10.(2022春·浙江金华·八年级统考期末)测试五位学生的“一分钟仰卧起坐”成绩,得到五个各不相同的数据. 在统计时,出现了一处错误:将最高成绩50个写成了55个.则下列统计量不受影响的是( )
A.方差 B.标准差 C.中位数 D.平均数
二、解答题
11.(2022春·浙江湖州·八年级统考期末)某单位450名职工积极参加想贫困地区捐书活动,为了解职工的捐书两,采用随机抽样的方法抽取了30名职工作为样本,对他们的涓蜀梁进行统计,统计结果共有4本,5本,6本,7本,8本,五类,分别用A,B,C,D,E表示,根据统计数据绘制成了如图所示不完整的条形统计图,用图中所给的信息解答下列问题:
(1)补全条形统计图;
(2)求这30名职工捐书本书的平均数;
(3)估计该单位450名职工共捐书多少本?
12.(2022春·浙江金华·八年级统考期末)学校准备从甲乙两位选手中选择一位,代表学校参加所在地区的汉字听写大赛,总评成绩由“表达能力、阅读理解、综合素质和汉字听写”四部分组成.甲,乙两位选手的成绩如下表,请解答下列问题:
选手 表达能力 阅读理解 综合素质 汉字听写
甲 85 78 85 73
乙 73 80 82 83
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩.
(2)已知四部分占总评成绩的比例如图所示.
①求图中表示“阅读理解”的扇形的圆心角度数;
②通过计算甲,乙两名选手的总评成绩,你认为学校派谁参加比赛合适?
13.(2022春·浙江衢州·八年级统考期末)北京冬奥会女子大跳台决赛的打分规则;6名裁判打分,去除一个最高分和一个最低分,剩余4个分数的平均值为该选手成绩.下表是中国选手谷爱凌第一跳的得分情况,其中裁判4,裁判5的打分(分别为94分和a分)被去除.
裁判1 裁判2 裁判3 裁判4 裁判5 裁判6 成绩
94分 94分 94分 b分 93.75分
请根据表中信息,解决以下问题;
(1)求b的值.
(2)判断a是否最低分并说明理由.
(3)从平均数的特征说说打分规则中去除一个最高分及一个最低分的合理性.
14.(2022春·浙江杭州·八年级统考期末)某公司要招聘一名职员,根据实际需要,从学历、经验、能力和态度四个方面对甲、乙、丙三名应聘者进行了测试,测试成绩如下表.
项目 应聘者
甲 乙 丙
学历 9 8 8
经验 8 6 9
能力 7 8 8
态度 5 7 5
(1)如果将学历、经验、能力和态度四项得分按1∶1∶1∶1的比例确定每人的最终得分,并以此为依据确定录用者,那么谁将被录用?
(2)如果你是这家公司的招聘者,请按你认为的各项“重要程度”设计四项得分的比例,以此为依据确定录用者,并说一说你这样设计比例的理由.
15.(2022春·浙江宁波·八年级统考期末)某社区为了增强居民节约用水的意识,随机调查了部分家庭一年的月均用水量(单位:t).
根据调查结果,绘制出如下的统计图①和图②.
请根据相关信息,解答下列问题:
(Ⅰ)本次接受调查的家庭个数为________,图①中m的值为_______;
(Ⅱ)求统计的这组月均用水量数据的平均数、众数和中位数.
16.(2022春·浙江舟山·八年级统考期末)某中学八年级组织了一次“汉字听写比赛”,每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中A等级得分为100分,B等级得分为85分,C等级得分为75分,D等级得分为60分,语文教研组将八年级一班和二班的成绩整理并绘制成如下的统计图,请根损换供的信息解答下列问题.
(1)把一班比赛成统计图补充完整;
(2)填表:
平均数(分) 中位数(分) 众数(分)
一班 a b 85
二班 84 75 c
表格中:a=______,b=______,c=_______.
(3)请从以下给出的两个方面对这次比赛成绩的结果进行分析:
①从平均数、众数方面来比较一班和二班的成绩;
②从B级以上(包括B级)的人数方面来比较-班和二班的成绩.
17.(2022春·浙江温州·八年级统考期末)某校八(1)班有40名学生,他们2021年纸质书阅读情况如图所示.
(1)求这40名学生纸质书阅读量的平均数、中位数和众数.
(2)班级拟进行“个人阅读达标奖”评比,为了提高学生的阅读积极性且使超过50%的同学能达标.如果你是决策者,从平均数、中位数和众数的角度进行分析,你将如何确定这个“达标标准”?
18.(2022春·浙江台州·八年级统考期末)杨梅销售公司在向果农收购相同品种“东魁”杨梅时,按照杨梅单果质量(单位:g)的整体分布情况,确定整批杨梅的等级,并按照不同的等级确定不同的收购价.
果农老张和老王各送来一批杨梅,收购员小李在他们送来的杨梅中分别随机抽检了100颗,秤出质量(单位:g),并把收集到的数据整理成下表:
杨梅单果质量(g) 二等() 一等() 优等() 特优()
组中值 17.5 22.5 27.5 32.5
老张家杨梅数量(个) 20 32 26 22
老王家杨梅数量(个) 14 26 36 24
(1)若用扇形图描述老王家各个等级杨梅的比例,其表示特优杨梅的扇形的圆心角是_______°.
(2)从杨梅单果质量的平均数看,你认为老张家杨梅的收购价与老王家杨梅的收购价应该相同吗?请说明理由.
(3)结果,收购员小李给老张家杨梅定的收购价比老王家的杨梅收购价低一个等级,你能用统计知识解释小李这样做的合理性吗?
19.(2022春·浙江宁波·八年级统考期末)毛泽东同志曾说“德志皆寄予于体,无体是无德志也”,某社区为了加强社区居民对冬奥会的了解,鼓励社区居民在线参与作答《2022年北京冬奥会知识点》模拟试卷,社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩(单位:分)进行统计、分析,过程如下:
【收集数据】
甲:85,80,95,100,90,95,85,65,75,85,89,90,70,90,100,80,80,90,96,75;
乙:80,60,80,95,65,100,90,85,85,80,95,75,80.90,70,80,95,75,100,90.
【整理数据】
成绩x 60≤x≤70 70<x≤80 80<x≤90 90<x≤100
甲小区 2 5 a b
乙小区 3 7 5 5
【分析数据】
统计量 平均数 中位数 众数
甲小区 85.75 87.5 c
乙小区 83.5 d 80
【应用数据】
(1)填空:a= ,b= ,c= ,d= ;
(2)若甲小区共有600人参与答卷,请估计甲小区成绩大于80分的人数;
(3)你认为甲、乙两个小区哪一个对冬奥会知识掌握更好?请写出一条理由.
20.(2022春·浙江杭州·八年级统考期末)某次数学测试,圆圆同学所在的学习小组其他同学的平均分为75分,圆圆说,“我的分是100分,我们学习小组的平均分恰好是80分”.
(1)圆圆同学所在的学习小组具有多少人?
(2)已知该学习小组本次测试得分的众数是90分,最低分为50分,求该学习小组本次测试得分的中位数.
21.(2022春·浙江金华·八年级统考期末)按照疫情防控工作部署,学校核酸检测有序进行,已知检测员甲和检测员乙到某校进行核酸检测,分别记录两人检测前6名学生所用的时间,获得如下检测时间折线统计图,根据图中信息,解答下列问题:
(1)要评价每位检测员检测时间平均水平,你选择什么统计量?求这个统计量.
(2)求检测员乙检测时间的方差.
(3)现求得检测员甲检测时间的方差(单位:平方秒)根据折线统计图及上面两个小题的计算,你认为哪位检测员的检测技术比较娴熟?请简述理由.
22.(2022春·浙江绍兴·八年级统考期末)2022年冬奥会在北京举行,为了增进学生对冰雪文化的了解,我校开展了冰雪运动相关知识的宣传教育活动,提高了学生对冰雪运动的关注度,并掀起了模拟冰雪运动的热潮.在模拟冰壶比赛中,规定得6分及以上为合格,得8分及以上为优秀.学校从参加比赛的七、八年级学生中各随机抽取了15名学生的比赛成绩,他们的成绩如下表:
成绩(分) 4 5 6 7 8 9
七年级(人) 1 2 5 2 1 4
八年级(人) 1 1 4 5 2 2
模拟冰壶比赛得分统计如下:
统计量平均分中位数众数方差合格率
统计量 平均分 中位数 众数 方差 合格率
七年级 6.8 m 6 2.56 80.0%
八年级 6.8 7 n 1.76 86.7%
(1)m=_______;n=_________;
(2)你认为哪个年级的模拟冰壶比赛成绩更优秀?请说明理由;
(3)若七、八年级参加模拟冰壶比赛的人数分别600人和450人,求这两个年级共有多少学生的模拟冰壶比赛成绩为优秀等级?
三、填空题
23.(2022春·浙江温州·八年级统考期末)已知一组数据2,1,,6的平均数是4,则的值为_______.
24.(2022春·浙江金华·八年级统考期末)某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为95分、85分、90分,综合成绩按笔试、试讲、面试的占比为2:2:1,则该名教师的综合成绩为_____.
25.(2022春·浙江宁波·八年级统考期末)2021年6月17日,中国第7艘载人航天飞船“神舟12号”圆满发射成功,激励更多的年轻人投身航天事业.现对学员们进行招飞前考核,其中某位学员心理素质、身体素质、科学头脑、应变能力四项测试得分分别为86分、85分、88分、90分,若按照心理素质、身体素质、科学头脑、应变能力的占比为4∶3∶2∶1的比例确定总分,则该名学员的总分为______________分.
26.(2022春·浙江湖州·八年级统考期末)若一组数据1,5,2,3,x,y的平均数为3,众数也为3,则这组数据的中位数为_________.
27.(2022春·浙江湖州·八年级统考期末)某人5次射击命中的环数分别为5,10,7,x,10,若这组数据的中位数为8,则这组数据的方差为________.
28.(2022春·浙江台州·八年级统考期末)甲、乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差s2甲与s2乙的大小关系是s2甲_______s2乙.(填“>”或“<”)
29.(2022春·浙江金华·八年级统考期末)某天的最低气温是﹣2℃,最高气温是10℃,则这天气温的极差为_____℃.
参考答案:
1.D
【分析】根据众数和中位数的定义进行求解即可得出答案.
【详解】解:根据题意可得,参加体育锻炼时间的众数为7,
因为该班有40名同学,所以中位数为第20和21名同学时间,第20名同学的时间为,第21名同学的时间为,
所以中位数为.
故选:D.
【点睛】考查了中位数、众数的概念.本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
2.C
【分析】将这组数据从小到大重新排列,再根据中位数的定义求解即可.
【详解】将这组数据从小到大重新排列为23,25,27,29,
∴这组数据的中位数为,
故选:C.
【点睛】本题主要考查中位数,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
3.D
【分析】根据中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)的意义,9人成绩的中位数是第5名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.
故选:D.
【点睛】本题考查了统计量的选择,熟练掌握众数,方差,平均数,中位数的概念是解题的关键.
4.B
【分析】根据中位数的定义求解即可.
【详解】去掉一个最高分和一个最低分对中位数没有影响.
故选:B.
【点睛】本题考查了统计量的选择,解题的关键是了解中位数的定义.
5.C
【分析】出现次数最多的数据是样本的众数,根据定义解答.
【详解】解:∵4.7出现的次数最多,∴视力的众数是4.7,
故选:C.
【点睛】此题考查了众数的定义,熟记定义是解题的关键.
6.C
【分析】根据各个选项的意义进行判断即可得到答案.
【详解】观察各个尺码的鞋的销售量知,尺码为23.5厘米的鞋销售量最多,
即影响鞋店决策的统计量是众数.
故选:C.
【点睛】本题考查统计的相关知识,掌握平均数、中位数、众数、方差的意义是关键.
7.B
【分析】利用已知条件可知统计时误将一位学生的成绩65分记成了60分,平均数和方差都要变,可对A,D作出判断;同时众数也要变化,可对C作出判断;此时的中位数不变,可对B作出判断.
【详解】解:∵6位学生的成绩分别为65分,65分,80分,85分,90分,90分,统计时误将一位学生的成绩65分记成了60分,
∴众数要变,故C不符合题意;平均数与每个数有关,因此平均数也要变,故A不符合题意;方差与每个数据有关,数据变了方差也要变化,故D不符合题意;中位数是82.5,不会变化,故B符合题意;
故答案为:B.
【点睛】本题考查了平均数;中位数;方差;众数等知识,掌握平均数、方差、中位数、众数的含义是解题的关键.
8.A
【分析】根据平均数和方差的变化规律,即可得出答案.
【详解】解:由题意得,数据的平均数为,
=
=
=
=18,
∵方差为2,
∴的方差不变,也是2,
故选:A.
【点睛】本题考查了方差与平均数,用到的知识点:如果一组数据的平均数为,方差为,那么另一组数据的平均数为,方差为,熟练掌握相关知识点是解题关键 .
9.A
【分析】根据平均数反映了成绩的好差,方差反映数据的稳定性.选择成绩好且发挥稳定,选择平均数大,方差小的选手,即可.
【详解】∵平均数:,方差:,选择平均数大,方差小的值
∴选择甲.
故选:A.
【点睛】本题考查平均数、方差,灵活掌握平均数,方差在数据中运用是解题的关键.
10.C
【分析】根据中位数的定义解答可得.
【详解】解:因为中位数是将数据按照大小顺序重新排列,代表了这组数据值大小的“中点”,不受极端值影响,
所以将最高成绩写得更高了,50个写成了55个,计算结果不受影响的是中位数,
故选:C.
【点睛】本题主要考查方差、极差、中位数和平均数,解题的关键是掌握中位数的定义.
11.(1)见解析
(2)这30名职工捐书本数的平均数为6本
(3)估计该单位450名职工共捐书2700本
【分析】(1)根据题目中的数据和条形统计图中的数据,可以计算出捐D类书的人数,从而可以将条形统计图补充完整;
(2)根据条形统计图中的数据,可以计算出平均数;
(3)根据(2)中的平均数,可以计算出该单位450名职工共捐书多少本.
【详解】(1)捐D类书的有30﹣4﹣6﹣9﹣3=8(人),
补全的条形统计图如下图所示:
(2)(4×4+5×6+6×9+7×8+8×3)=6(本),
答:这30名职工捐书本数的平均数为6本.
(3)450×6=2700(本),
答:估计该单位450名职工共捐书2700本.
【点睛】本题主要条形统计图画法、求平均数、用样本估计总体等知识,理解掌握相关概念与计算公式是解题关键.
12.(1)79.5
(2)①;②学校派乙参加比赛合适
【分析】(1)根据平均数的定义求解即可;
(2)①用360度乘以阅读理解的占比即可得到答案;②分别求出甲、乙两人的总成绩即可得到答案.
(1)
解:由题意得,乙的平均成绩为;
(2)
解:①由题意得:
图中表示“阅读理解”的扇形的圆心角度数为
②甲的总成绩为:,
乙的总成绩为:,
∵80.4>79.5,
∴学校派乙参加比赛合适.
【点睛】本题主要考查了求平均数,求加权平均数,求扇形圆心角度数,利用平均数做决策等等,正确理解题意是解题的关键.
13.(1)93
(2)a是最低分,只有当a≤93符合题意,否则就不满足平均数是93.75,且去掉的是94分和a分;
(3)由于平均数容易受到极端值的影响而发生变化,因此去除一个最高分及一个最低分可以避免平均数受极端值的影响.
【分析】(1)根据平均数的计算方法进行计算即可;
(2)根据计算成绩的方法进行判断即可;
(3)根据影响平均数的因素进行判断即可.
【详解】(1)解:由题意得,
解得b=93,
答:b的值为93;
(2)解:a是最低分,由题意可知a≤93,否则就不满足平均数是93.75,且去掉的是94分和a分;
(3)解:由于平均数容易受到极端值的影响而发生变化,因此去除一个最高分及一个最低分可以避免平均数受极端值的影响.
【点睛】本题考查算术平均数,理解平均数的意义,掌握平均数的计算方法是解决问题的前提.
14.(1)丙将被录用
(2)见解析
【分析】(1)计算算术平均数即可;
(2)计算加权平均数即可.
【详解】(1)解:依题意,
甲的平均分为,
乙的平均分为,
丙的平均分为,
则丙的平均分最高,因此丙被录用.
(2)解:如果将学历、经验、能力和态度四项得分按3:2:3:2的比例确定每人的最终得分,
则甲的得分为,
乙的得分为,
比丙的得分为,
丙的得分最高,因此丙被录用.
理由:因为数据中的“权”反映数据的相对“重要程度”,权越大,该数据占的比重越大,反之则越小.
【点睛】本题考查了算术平均数、加权平均数,熟练掌握加权平均数的意义和计算公式是解答的关键.
15.(Ⅰ)50,20;(Ⅱ)这组数据的平均数是5.9;众数为6;中位数为6.
【分析】(Ⅰ)利用用水量为5t的家庭个数除以其所占百分比即可求出本次接受调查的家庭个数;利用用水量为6.5t的家庭个数除以本次接受调查的家庭个数即得出其所占百分比,即得出m的值.
(Ⅱ)根据加权平均数的公式,中位数,众数的定义即可求出结果.
【详解】(Ⅰ)本次接受调查的家庭个数=,
由题意可知 ,
解得.
故答案为50,20.
(Ⅱ)观察条形统计图,
∵,
∴这组数据的平均数是5.9.
∵在这组数据中,6出现了16次,出现的次数最多,
∴这组数据的众数为6.
∵将这组数据按从小到大的顺序排列,其中处于中间的两个数都是6,
即有,
∴这组数据的中位数为6.
【点睛】本题考查条形统计图与扇形统计图相关联,加权平均数,中位数以及众数.从条形统计图与扇形统计图中找到必要的数据和信息是解答本题的关键.
16.(1) 统计图补充完整如图所示见解析;(2)二班的平均数为:a=82.8 ,一班的中位数为:b=85, 二班的众数为:c=100 ; (3)①从平均数和众数的角度来比较二班的成绩更好;②从B级以上(包括B级)的人数的角度来比较一班的成绩更好.
【分析】(1)根据题意和表格中的数据可以求得一班C等级的学生数,从而可以解答本题;
(2)根据表格中的数据可以求得一班的平均数和中位数,以及二班的众数;
(3)根据表格中的数据,可以从两方面比较一班和二班成绩的情况.
【详解】解:(1)一班中C级的有25-6-12-5=2人
如图所示
(2) 一班的平均数为:a= =82.8,
一班的中位数为:b=85
二班的众数为:c=100 ;
(3)①从平均数和众数的角度来比较二班的成绩更好;
②从B级以上(包括B级)的人数的角度来比较一班的成绩更好.
故答案为(1) 统计图补充完整如图所示见解析;(2)二班的平均数为:a=82.8 ,一班的中位数为:b=85, 二班的众数为:c=100 ; (3)①从平均数和众数的角度来比较二班的成绩更好;②从B级以上(包括B级)的人数的角度来比较一班的成绩更好.
【点睛】本题考查条形统计图、扇形统计图、众数、中位数、加权平均数,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
17.(1)平均数是6.5、中位数是6、众数是5
(2)选择中位数作为标准,理由见解析
【分析】(1)根据40名学生纸质书阅读量总数除以总人数,求得平均数;中位数就是大小处于中间位置的数,众数就是出现次数最多的数,根据定义判断即可;
(2)根据求出的这40名学生阅读量的平均数、中位数和众数的角度,各个角度分析即可.
(1)
解:平均数:,
中位数,
众数是5;
(2)
当标准为平均数6.5本,达到标准的学生有19人未超过50%;
当标准为中位数6本,达到标准的学生有26人超过50%,有利于提高学生的积极性;
当标准为众数5本,40名学生都达到标准,但不利于提高学生的积极性;
因此应该选择中位数作为标准.
【点睛】本题考查的是统计的应用,读懂统计表,从统计表中得到必要的信息是解决问题的关键.本题也考查了平均数、中位数、众数的认识.
18.(1)86.4
(2)应该相同,理由见解析
(3)见解析,理由见解析
【分析】(1)用360°乘以老王家特优杨梅的频率即可;
(2)分别求出两家的平均数,即可比较出来;
(3)根据所求数据进行分析即可.
【详解】(1)解:360°×=86.4°,
故答案为:86.4;
(2)解:老张家杨梅的等级的平均数为(克)
老王家:(克)
从平均数看,根据样本估计总体,老张家与老王家的杨梅单颗质量平均数落在同一级别中,所以两家收购价应该相同;
(3)解:从中位数角度来看,根据样本估计总体,老张家的杨梅单颗质量中位数落在组,属于一等品;而老王家的杨梅单颗质量中位数落在组,属于优等品,因此收购员小李给老张家杨梅定的收购价比老王家的杨梅收购价低一个等级也是合理的.
【点睛】本题考查扇形统计图,平均数及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.
19.(1)8;5;90;82.5;
(2)390人;
(3)甲小区,理由见解析.
【分析】(1)直接根据收集的数据以及众数、中位数的定义求解即可;
(2)用600乘以甲小区成绩大于80分的人数所占比例即可;
(3)直接比较两小区的平均数、中位数、众数即可.
(1)
由甲小区抽取的20名人员的答卷成绩可知a=8,b=5,
甲的数据:85,80,95,100,90,95,85,65,75,85,89,90,70,90,100,80,80,90,96,75;
从中可以得出数据90出现的次数最多,得出c=90,
把乙小区抽取的20名人员的答卷成绩排序为:60,65,70,75,75,80,80,80,80,80,85,85,90,90,90,95,95,95,100,100,
则乙小区成绩的中位数为=82.5(分),
故答案为:8,5,90,82.5;
(2)
估计甲小区成绩大于80分的人数为600×=390(人)
(3)
甲小区对冬奥会知识掌握更好,
理由:甲小区的平均数、中位数、众数均大于乙小区的.
【点睛】本题主要考查统计图表及数据的收集宇整理知识,熟练掌握众数、平均数、中位数的定义、用样本估计总体的方法是解题的关键.
20.(1)圆圆同学所在的学习小组有5人;
(2)该学习小组本次测试得分的中位数是90分.
【分析】(1)利用平均数的定义直接计算即可;
(2)利用众数,中位数的定义即可求解.
【详解】(1)解:根据题意得:(100- 75) ÷ (80- 75)= 5(人),
∴圆圆同学所在的学习小组有5人;
(2)解:该学习小组有5人,最低分为50分,圆圆的分是100分,
∵众数是90分,
∴本次测试得分是90分的有2人,最低分为50分,
∴该学习小组本次测试还有一个得分是80×5-(50+ 90×2+100)= 70(分),
∴该学习小组本次测试得分从小到大排列为50,70,90, 90,100,
∴该学习小组本次测试得分的中位数是90分.
【点睛】本题考查的是平均数,众数,中位数,弄清题意是解本题的关键.
21.(1)平均值,,
(2)
(3)检测员乙的检测技术较娴熟,见解析
【分析】(1)根据题意,要评价每位检测员检测时间平均水平,选择平均数,根据折线统计图求得甲、乙的数据,进而求得平均数即可求解;
(2)根据方差公式进行计算即可求解;
(3)比较甲乙的方差大小即可求解.
【详解】(1)解:∵要评价每位检测员检测时间平均水平,
∴选择平均数,
根据统计图可知,甲:7,6,6,9,10,10,
平均数为,
乙:7,8,7,10,7,9,
,
(2);
(3)检测员乙的检测技术较娴熟,理由如下,
,,,,
,
检测员乙的检测技术较娴熟.
【点睛】本题考查了折线统计图,选择合适的统计量,求平均数,求方差,掌握以上知识是解题的关键.
22.(1)6;7
(2)八年级的模拟冰壶比赛成绩更优秀,理由见解析
(3)320
【分析】(1)根据一组数据按从小到大或从大到小的顺序排列后中间的数叫做中位数,出现次数最多的数叫做众数,即可求解;
(2)从平均成绩、众数、方差、合格率几方面分析,即可求解;
(3)分别求出七年级和八年级的比赛成绩为优秀等级人数,即可求解.
(1)
解:∵七年级15人的成绩的第8个数为6分,
∴七年级15人的成绩的中位数为6分,即m =6;
∵八年级15人的成绩中最多的是7分,
∴众数为7分,即n=7,
故答案为:6;7;
(2)
八年级的模拟冰壶比赛成绩更优秀,理由如下:
从平均成绩看,两个年级的成绩一样,从中位数看,八年级的成绩好些,从众数看,八年级成绩更好,从方差看,八年级成绩的方差小于七年级成绩的方差,方差越小,成绩越稳定,故八年级成绩比七年级成绩稳定,从合格率看比年级成绩的合格率比七年级成绩的合格率高,综合以上几点,我认为八年级的模拟冰壶比赛成绩更优秀;
(3)
解: .
【点睛】本题主要考查了求中位数和众数,利用方差、平均数、中位数做决策,利用样本求总体数量等知识,熟练掌握相关知识点是解题的关键.
23.7
【分析】利用平均数的定义,列出方程即可求解.
【详解】∵一组数据2,1,,6的平均数是4,
∴,
解得,
故答案为:7.
【点睛】本题主要考查了平均数的概念、解一元一次方程.平均数是指在一组数据中所有数据之和再除以数据的个数,熟练掌握知识点是解题的关键.
24.90分
【分析】计算出该教师的加权平均数即可.
【详解】由题意知,该名教师的综合成绩为:(分),
故答案为:90分
【点睛】本题考查了加权平均数,掌握加权平均数的计算公式是关键.
25.86.5
【分析】根据加权平均数的公式进行计算即可求解,加权平均数计算公式为:,其中代表各数据的权.
【详解】解:∵得分分别为86分、85分、88分、90分,按占比为4∶3∶2∶1的比例确定总分,
∴该名学员的总分为
故答案为:86.5
【点睛】本题考查了求加权平均数,掌握加权平均数的计算公式是解题的关键.
26.3
【分析】根据这组数据的众数为3,可确定x和y中至少有一个值为3,再根据平均数为3即可确定另一个值,从而根据中位数的定义求出结果.
【详解】∵这组数据的众数为3,
∴x和y中至少有一个值为3.
∵平均数为3,假设x=3,
∴,
解得:,
∴这组数据按从大到小排列为1,2,3,3,4,5,且符合题意,
∴这组数据的中位数为.
故答案为:3.
【点睛】本题考查平均数、众数和中位数的定义.由平均数和众数具体的求出这组数据是解题关键.
27.3.6
【分析】根据中位数的性质,得;再根据方差的性质计算,即可得到答案.
【详解】根据题意,
∴5次射击命中的环数分别为5,10,7,8,10
∴这组数据的平均数为:
∴这组数据的方差为:
故答案为:3.6.
【点睛】本题考查了数据分析的知识;解题的关键是熟练掌握中位数、方差的性质,从而完成求解.
28.>
【分析】利用方差反映一组数据的波动大小的一个量进行判断.
【详解】解:∵甲地日平均气温的比乙地的日平均气温的变化幅度大,
∴方差s2甲>s2乙.
故答案为>.
【点睛】本题考查了方差:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
29.12
【详解】极差是指一组数据中最大数据与最小数据的差,因此,极差=10℃﹣2℃=12℃.
故答案为:12.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
